🌈 个人主页:十二月的猫-CSDN博客
🔥 系列专栏: 🏀算法启示录💪🏻 十二月的寒冬阻挡不了春天的脚步,十二点的黑夜遮蔽不住黎明的曙光
目录
前言
第二十五章
25.1-10
25.2-5
25.2-6
第二十六章
26.2-2
26.2-4
26.3-4(较难)
总结
前言
算法导论的知识点学习将持续性更新在算法启示录_十二月的猫的博客-CSDN博客,欢迎大家订阅呀(反正是免费的哦~~)
实战篇也将在专栏上持续更新,主要目的是强化对理论的学习(题目来源:山东大学孔凡玉老师推荐)

第二十五章
25.1-10
问题描述:
给出一个有效算法来在图中找到最短长度的权重为负值的环路的长度(边的条数)
问题分析:
我们学过的所有图算法有贝尔曼福特、迪杰斯特拉、弗洛伊德以及一般动态规划求解多源最短路径算法。
在这里面迪杰斯特拉不允许有负值权重,贝尔曼福特仅仅能处理单源最短路径。弗洛伊德相比于一般动态规划算法具有简洁明了、运行稳定等优点,所以我们选用弗洛伊德算法来处理。
问题求解:
明确一个点:
1、如果dist[i,i]<0,那么表示图中存在负值环路
2、存在负值环路时,前驱矩阵仍然有效,我们可以通过前驱矩阵来确定负值环路的长度
25.2-5
问题描述:

问题分析:
首先,要理解这个修改的含义是什么?
将等号从上一种情况挪用到下一种情况,问是否正确,本质就是在问:
dij(k−1)=dik(k−1)+dkj(k−1)时前驱矩阵应该要执行哪个操作
dij(k−1)=dik(k−1)+dkj(k−1)意味着无论是否经过k点长度是相同的,根据三角形理论我们知道这个等号成立的唯一情况就是:顶点k在路径上的另外两点连线上
所以问题就转为:顶点k在路径上的另外两点连线上时,前驱矩阵生成要执行哪个操作
问题求解:

显然,是正确的,两种操作都可行
25.2-6
问题描述:
我们怎样才能使用 Floyd-Warshall 算法的输出来检测权重为负值的环路?
问题求解:
弗洛伊德算法的输出有两个:一个是点与点之间的最短路径长度矩阵;另一个是前驱子图矩阵。
假如存在i使得dist[i,i]<0,那么就代表存在权重为负值的环路
第二十六章
26.2-2
问题描述:
![]()
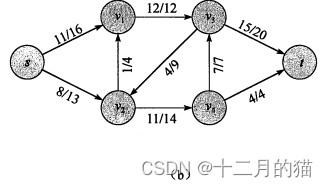
问题分析:
需要先明白横跨切割是什么意思,见下图:
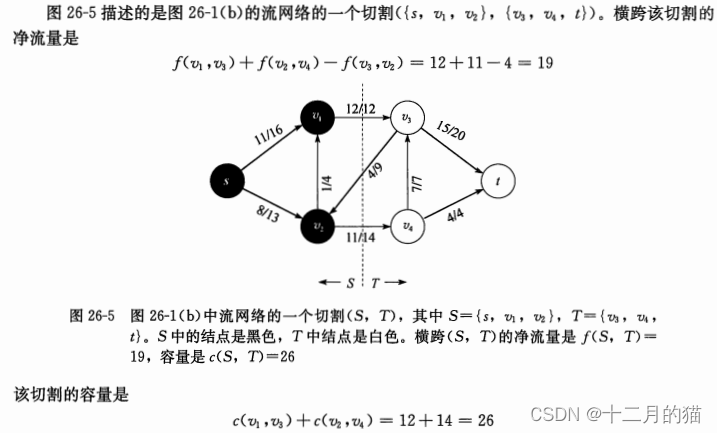
切割:将图切割为两个部分,利用两个{}符号来表示切割后图的两个部分
问题求解:
图分为两个部分{s、v2、v4}、{v1、v3、t}:
计算得到
流:11+1-4+7+4=19
容量:16+4+7+4=31
注意:在容量计算时,不考虑反向边的流
26.2-4
问题描述:
在图 26-6 的例子中,对应图中所示最大流的最小切割是什么?在例子中出现的增广路径里,哪一条路径抵消了先前被传输的流?
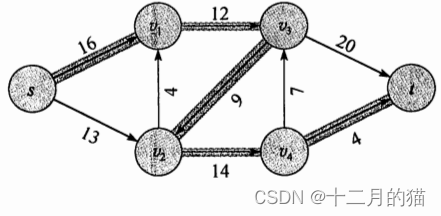
问题分析:
一个问题:最大流的最小切割是什么?
这涉及到一个定理 最大流最小切割定理

直觉理解:一个流网络中最大流的值不能超过该网络最小切割的容量(推论26.5)
推论26.5证明如下:

问题求解:
利用FORD-FULKERSON算法可以知道:最大流为23。又通过最大流最小切割定理可以知道:
这个最大流的值必然等于图中的一个最小切割
因此最小切割为S={s,v1,v2,v4} and 𝑇={𝑣3,𝑡}
同时(v2,v3)抵消了原本的流
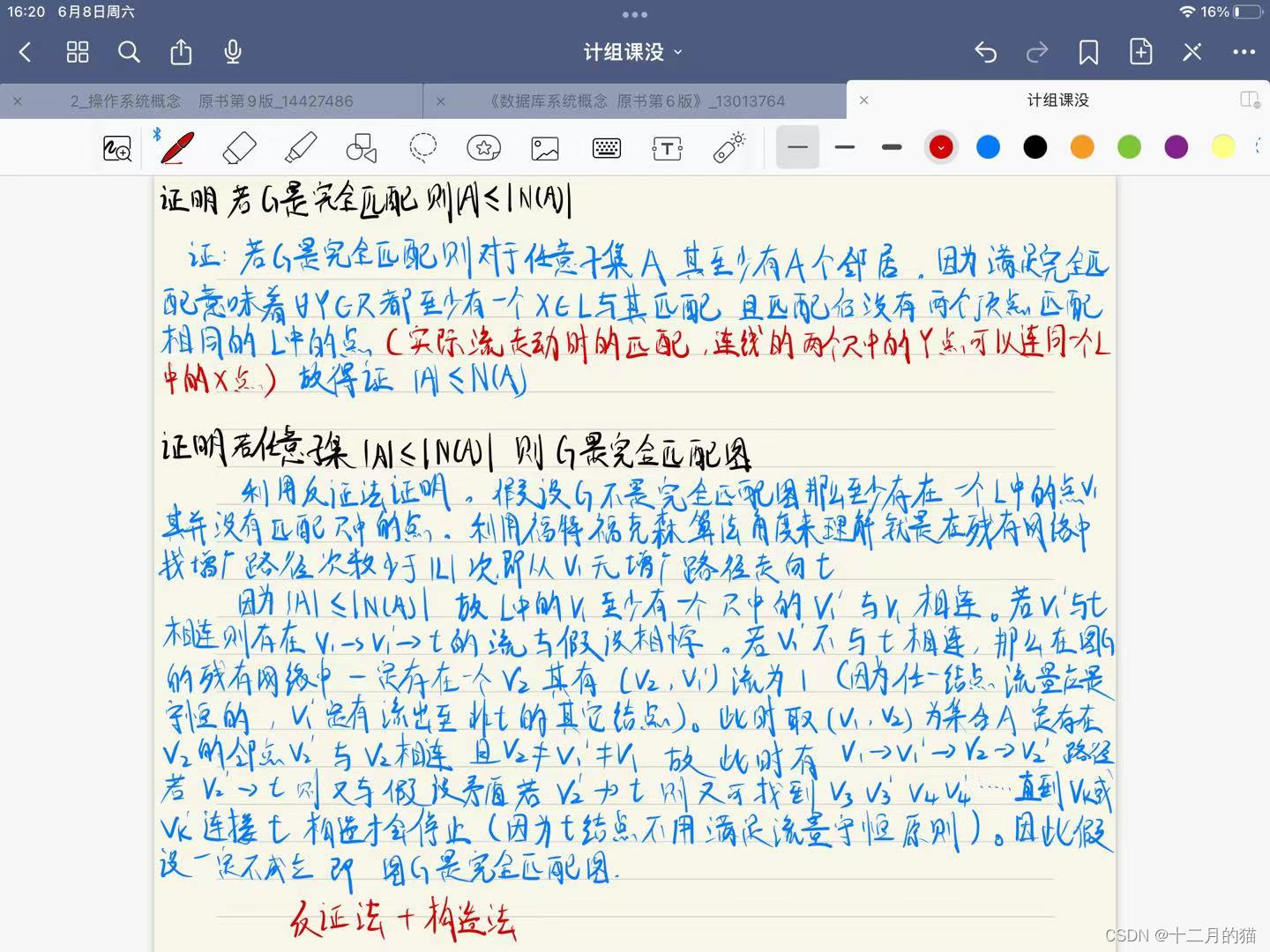
26.3-4(较难)
问题描述:

问题分析:
本题需要证明当且仅当的关系,所以证明分为两个方向一个是必要性一个是充分性
需要证明:
1、如果A<=N(A),那么图G是完全匹配图
2、如果图G是完全匹配图,那么A<=N(A)
问题求解:
总结
本文到这里就结束啦~~
本篇文章看起来字数少,但是有几道题目的难度还是比较大的,尤其是26.3-4的证明题(利用了构造法+反证法证明)
本篇文章的撰写花了本喵四个多小时
如果仍有不够,希望大家多多包涵~~
如果觉得对你有帮助,辛苦友友点个赞哦~

知识来源:《算法导论》课后习题、山东大学孔凡玉老师ppt。不要用于商业用途转发~





![[Vue3:axios]:实现实现登陆页面前后端请求,并用Vite解决跨域问题](https://img-blog.csdnimg.cn/direct/3a8ce1fbf345438aafe0060c48a79751.png)