一、定义
计数排序(CountSort)是一种非比较的排序,它的优势在于在对一定范围内的整数排序时,它的时间夫扎渡为为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。 这是一种通过空间换取时间的算法,但是当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序(基于比较的排序的时间复杂度在理论上的下限是O(n*log(n)), 如归并排序,、堆排序、快速排序)✨
二、思路:
1、确定范围,找出待排序数组✨ a[] 的最大值(max)和最小值(最小值)
2、申请一个计数的数组记为 ✨count[],并初始化为0,数组的大小由max-min+1决定(因为可以保证待排序所有的数都能记录上)🤔计数数组是什么个意思呢??🤔就是说我的计数数组,它的下标表示的是该值,然后,下标对应的元素表示该值在待排数组出现的次数✨

3、计数:遍历待排序的数组,进行计数,对于每个元素 x ,我们将count[x-min]的值加1,表示在原数组中值为x的元素出现了count[x-min]次;👉👉看看下面呗🥰
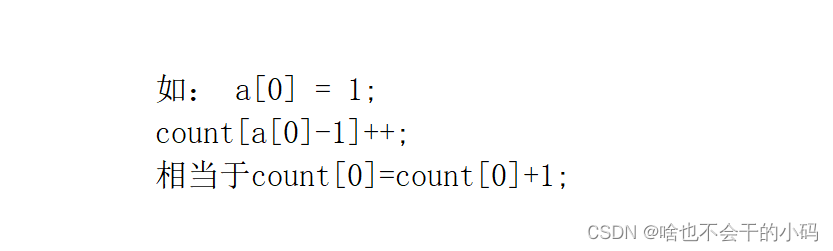
用当前元素 x - min 这样是为了进行相对映射,🤔因为我们数组的下标从0开始的,但是数据并不一定是从0开始的,如果我直接就是将 x的值来作为计数数组的下标,就会造成空间浪费的现象。用x-min的方式,可以将其记录在对应下标的位置处
4、排序:当遍历完待排序数组后,计数数组也就记录好数据了🐸🐸

✨那么也就最后一步了,排序嘛,遍历计数数组,根据每个下标对应的数据个数排序,通过计数将元素一一放入到数组a[] 中,注意是下标加min 因为之前是 小标是 x- min 计数的 放到a[],就是下标j+min;该下标对应的元素有几个 就对该下标放几次;因为这里都是只有一个的情况,所以我们都只放了一次,因为原数组没有 6 为0,所以没有放入

注意:计数排序只适用于整数,而且尽量是数据集中的,但是如果数据过于离散的话(数据范围很大)创建和维护数组需要消耗大量内存,那么此时该排序就未必好用了
三、时间复杂度:
时间复杂度 O(N+k) 取决于k 与 N 谁大
空间复杂度 O(k) 取决于max-min+1的大小
✨补充一句:它是稳定的,相等的元素在排序后的相对顺序不会改变✨
四、代码实现:
//计数排序:
void CountSort(int* a, int n)
{
//求最大和最小值
int max = a[0];
int min = a[0];
for (int i = 1; i < n; i++)
{
if (a[i] < min)
{
min = a[i];
}
if (a[i] > max)
{
max = a[i];
}
}
int ragem = max - min + 1;
//计数的数组
int* count = (int*)calloc(ragem, sizeof(int));;
if (count == NULL)
{
perror("calloc fail");
return;
}
//计数
for (int i = 0; i < n; i++)
{
count[a[i] - min]++;
}
int j = 0;
//排序
for (int i = 0; i< ragem; i++)
{
while (count[i]--)
{
a[j++] = i+ min;
}
}
}✨可以看一下,对1000万个数据进行排序,五种排序消耗的时间,计数是👉真的快
🧑🎓所以说在数据范围不是很大的情况下,计数快于需要进行比较的排序,真不是吹的 🤔
 拜 拜 喽
拜 拜 喽