混合背包的定义:
混合背包问题就是混合01背包、完全背包和多重背包,可供选择的物体i可能有一个、或者无数个、或者有限个。
所以,就不要考虑这么多了,直接分这三种情况考虑就行!!
样例:
for(int i=1;i<=n;i++)
{
//01背包
if(p[i]==1)
{
for(int j=time;j>=w[i];j--)
{
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
//完全背包
if(p[i]==0)
{
for(int j=w[i];j<=time;j++)
{
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
//多重背包
else
{
for(int j=time;j>=0;j--)
{
for(int k=0;k<=p[i]&&k*w[i]<=j;k++)
{
dp[j]=max(dp[j],dp[j-k*w[i]]+k*v[i]);
}
}
}
}P1833 樱花

题意:就是说给我一个时间(背包容量),然后有n种樱花树,每个樱花树有自己的时间(花费)以及美学值(价值),但是每个种类的樱花树,数量是不同的
思路:混合背包问题,当数量为1的时候是01背包,是0的时候是完全背包,其余情况是混合背包,这样就对了吗?当然不是,不用二进制优化就80分,所以我们需要对这种情况进行二进制优化,将多重背包分开为01背包,然后只区分是不是0即可
#include<bits/stdc++.h>
using namespace std;
string a;
string b;
int n;
int w[10005];
int v[10005];
int p[10005];
int dp[1005];
// 将时间型字符串转换为分钟数
int timeStringToMinutes(std::string timeString)
{
int hours, minutes;
char colon;
std::stringstream ss(timeString);
ss >> hours >> colon >> minutes;
return hours * 60 + minutes;
}
// 计算时间差
int solve(std::string time1, std::string time2)
{
int minutes1 = timeStringToMinutes(time1);
int minutes2 = timeStringToMinutes(time2);
return minutes2 - minutes1;
}
int main()
{
cin>>a;
cin>>b;
int time=0;
time=solve(a,b);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>w[i]>>v[i]>>p[i];
}
for(int i=1;i<=n;i++)
{
if(p[i]==0)
{
for(int j=w[i];j<=time;j++)
{
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
else
{
for(int k=1;k<=p[i];k++)
for(int j=time;j>=w[i];j--)
{
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
}
cout<<dp[time];
return 0;
}有依赖的背包
有依赖的背包问题是一种特殊的背包问题,其中的物品不是完全独立的,而是存在依赖关系
在有依赖的背包问题中,多个物品可以被视为一个复合物品,这些物品之间可能存在互斥关系(即,选择了一个就不能选择另一个)。同时,每个复合物品可能有多种选择方式。例如,一个复合物品可能包括主物品和一些附属物品,你可以选择只带主物品,也可以选择带主物品和一些或全部附属物品,这就产生了多种可能性。在解决这种问题时,需要考虑所有可能的组合,以找到最优解。
P1064 [NOIP2006 提高组] 金明的预算方案

题意:就是说有m种物品,每个物品都有自己的价格重要度,价值是价格乘以重要度,后面的q判断的是是否自己就是主件,或者说这个物品的主件是什么
思路:有依赖的背包的例题,我们可以去用一个数组去存储每个主件的附件有几个,然后进行01背包,找出选择的最大价值
#include<bits/stdc++.h>
using namespace std;
int n,m;
int dp[32005];
int mw[65];
int mv[65];
int fw[65][3];
int fv[65][3];
signed main()
{
cin>>m>>n;
int w,p,q;
for(int i=1;i<=n;i++)
{
cin>>w>>p>>q;
if(q==0)
{
mw[i]=w;
mv[i]=w*p;
}
else
{
fw[q][0]++;//用于统计第q个主键有几个附件
fw[q][fw[q][0]]=w;
fv[q][fw[q][0]]=w*p;
}
}
for(int i=1;i<=n;i++)
{
for(int j=m;j>=mw[i];j--)
{
dp[j]=max(dp[j],dp[j-mw[i]]+mv[i]);
if(j>=mw[i]+fw[i][1])
{
dp[j]=max(dp[j],dp[j-mw[i]-fw[i][1]]+mv[i]+fv[i][1]);
}
if(j>=mw[i]+fw[i][2])
{
dp[j]=max(dp[j],dp[j-mw[i]-fw[i][2]]+mv[i]+fv[i][2]);
}
if(j>=mw[i]+fw[i][1]+fw[i][2])
{
dp[j]=max(dp[j],dp[j-mw[i]-fw[i][1]-fw[i][2]]+mv[i]+fv[i][1]+fv[i][2]);
}
}
}
cout<<dp[m];
return 0;
}背包思想
就是单纯用到了01背包的一种思想,去进行问题的求解
P2904 [USACO08MAR] River Crossing S
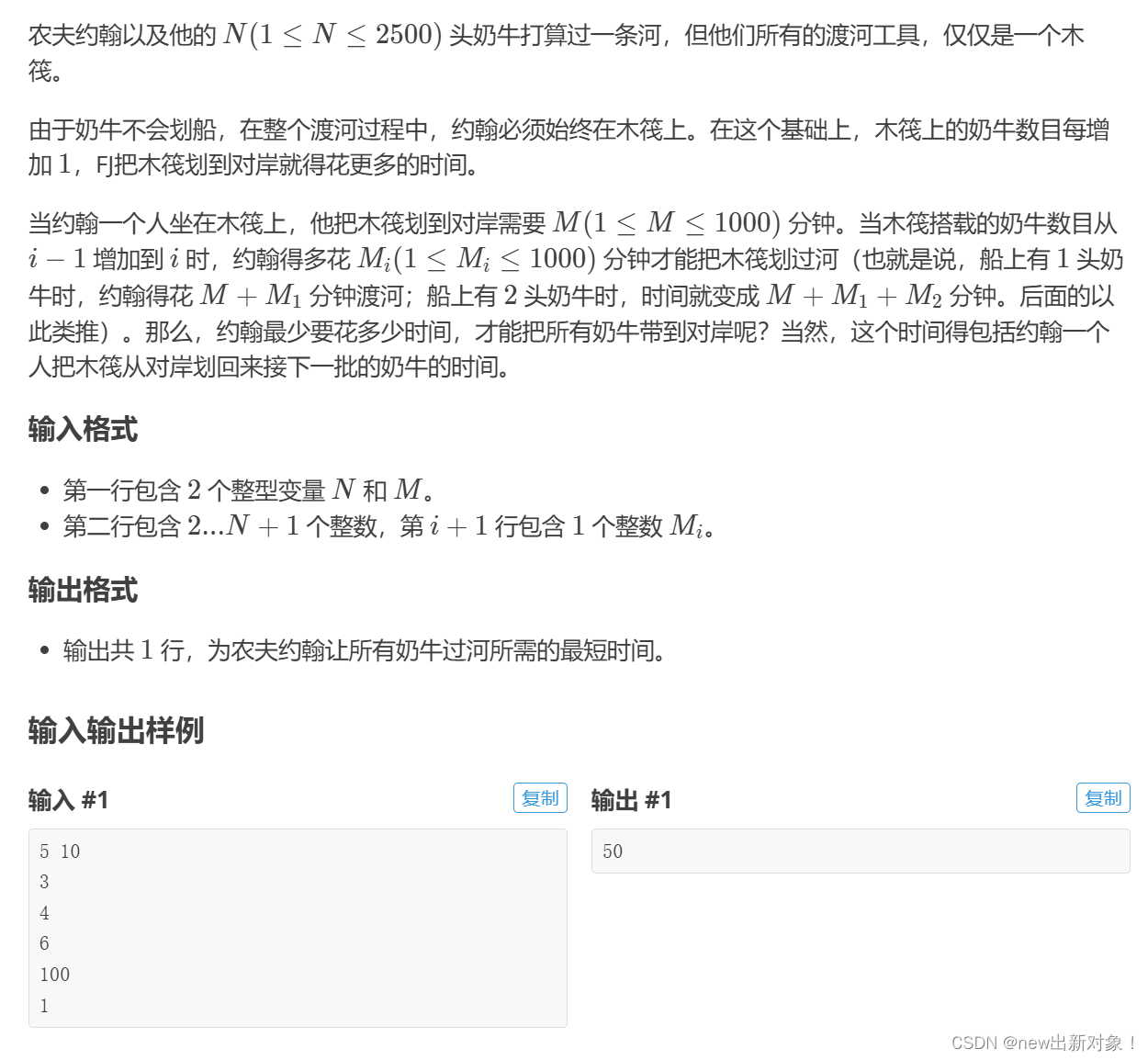
思路:就是将 每次运送n个奶牛作为时间作为花费,找出最小的时间(价值)
#include<bits/stdc++.h>
using namespace std;
int n,m;
int t[2505];
int pre[2505];
int dp[10005];
signed main()
{
cin>>n>>m;
memset(dp,0x3f3f3f3f,sizeof(dp));
dp[0]=0;
for(int i=1;i<=n;i++)
{
cin>>t[i];
pre[i]=pre[i-1]+t[i];
}
for(int i=1;i<=n;i++)
{
pre[i]+=2*m;
}
for(int i=1;i<=n;i++)
{
for(int j=i;j<=n;j++)
{
dp[j]=min(dp[j],dp[j-i]+pre[i]);
}
}
cout<<dp[n]-m<<"\n";
return 0;
}