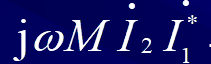目录
树的静态写法
树的先根遍历
树的层次遍历
从树的遍历看DFS和BFS
DFS与先根遍历
BFS与层次遍历
树的静态写法
这里讨论的树是一般意义上的树,即子结点个数不限且子节点没有先后次序的树。
建议使用静态写法进行结点的定义
struct node{
typename data;
int child[maxn];。。存放所有子节点的下标
}Node[maxn];在上面的定义中由于无法预知子结点个数,因此child数组的长度只能开到最大,而这对一些结点个数较多的题目来说显然是不可接受的,因此需要使用STL中的vector,即长度根据实际需要而自动变化的数组。
struct node{
typename data;
vector child;
}Node[maxn];当需要新建一个结点时,就按顺序从数组中取出一个下标即可。
int index=0;
int newNode(int v){
Node[index].data=v;
Node[index].child.clear();
return index++;
}树的先根遍历
树的先根遍历即总是先访问根节点,再去访问所有子树,递归访问。
void preorder(int root){
printf("%d ",Node[root].data);
for(int i=0;i<Node[root].child.size();i++){
preorder(Node[root].child[i]);
}
}树的层次遍历
树的层次遍历总是从树根开始,一层一层地向下遍历。
void Layerorder(int root){
queue<int> Q;
Q.push(root);
while(!Q.empty()){
int front=Q.front();
printf("%d ",Node[front].data);
Q.pop();
for(int i=0;i<Node[front].child.size();i++){
Q.push(Node[front].child[i]);
}
}
}同样地,如果需要对结点的层号进行求解,只需要在结构体node的定义中增加变量来记录结点的层号:
struct node{
int layer;
int data;
vector<int>child;
};于是树的层次遍历就可以写成下面这样:
void Layerorder(int root){
queue<int> Q;
Q.push(root);
Node[root].layer=0;//记录根结点的层号为0
while(!Q.empty()){
int front=Q.front();
printf("%d ",Node[front].data);
Q.pop();
for(int i=0;i<Node[front].child.size();i++){
int child=Node[front].child[i];
Node[child].layer=Node[front].layer+1;
Q.push(child);
}
}
}从树的遍历看DFS和BFS
DFS与先根遍历
例如当使用深度优先遍历搜索迷宫时,从入口出发,经过一系列岔道口和死胡同,最终找到了出口。事实上,可以把岔道口和死胡同都当作结点,并将它们的连接关系表示出来。
事实上所有合法的DFS求解过程,都可以把它画成树的形式,此时死胡同等价于树中的叶子结点,而岔道口等价于树中的非叶子节点,并且对这棵树的DFS遍历过程就是树的先根遍历的过程。
于是可以得到一些启发:碰到一些可以用DFS做的题目,不妨把一些状态作为树的结点,然后问题就会转换为直观的对树进行先根遍历的问题。如果想要得到树的某些信息,也可以借用DFS以深度作为第一关键词的思想来对结点进行遍历,以获得所需的结果。
BFS与层次遍历
在使用BFS模拟迷宫问题的过程中,依然将迷宫的岔道口和死胡同都简化为结点,将迷宫的结构转换为树。对所有合法的BFS求解过程,都可以转换为树的层次遍历的问题。
例题
给定一棵树和每个结点的权值,求所有从根节点到叶子节点的路径,使得每条路径上的结点的权值之和等于给定的常数S。如果有多条这样的路径,则按路径递增的顺序输出。其中路径的大小是指,如果两条路径的前几项都相等,遇到不等时,若,那么称第一条路径比第二条路径大。
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int maxn=110;
struct node{
int weigh;
vector<int> child;
}Node[maxn];
bool cmp(int a,int b){
return Node[a].weigh>Node[b].weigh;
}
int n,m,S;//结点数,边数,给定的和
int path[maxn];
//当前访问结点数index,numNode为当前路径path上的结点个数
void dfs(int index,int numNode,int sum){
if(sum>S){
return;
}
if(sum==S){
if(Node[index].child.size()!=0){
return;
}
for(int i=0;i<numNode;i++){
printf("%d",Node[path[i]].weigh);
if(i<numNode-1){
printf(" ");
}
else{
printf("\n");
}
}
return;
}
for(int i=0;i<Node[index].child.size();i++){
int child=Node[index].child[i];
path[numNode]=child;
dfs(child,numNode+1,sum+Node[child].weigh);
}
}
int main(){
scanf("%d%d%d",&n,&m,&S);
for(int i=0;i<n;i++){
scanf("%d",&Node[i].weigh);
}
int id,k,child;
for(int i=0;i<m;i++){
scanf("%d%d",&id,&k);//结点编号,孩子个数
for(int j=0;j<k;j++){
scanf("%d",&child);
Node[id].child.push_back(child);
}
sort(Node[id].child.begin(),Node[id].child.end(),cmp);
}
path[0]=0;
dfs(0,1,Node[0].weigh);
return 0;
}