LeetCode:295. 数据流的中位数

这个题目最快的解法应该是维护中位数,每插入一个数都能快速得到一个中位数。
根据数据范围,我们应当实现一个
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)的算法。
1、超时—插入排序
使用数组存储,维持数组有序,当插入一个元素时使用插入排序维持数组有序,这种方式无异于使用插入排序,时间复杂度不达标。
- 时间复杂度: O ( n 2 ) O(n^2) O(n2),由于每一个数都会被插入一次,插入一次的时间为 O ( n ) O(n) O(n)
- 空间复杂度:
O
(
n
)
O(n)
O(n)

class MedianFinder {
public:
MedianFinder() {}
void addNum(int num) {
nums.emplace_back(num);
for(int i = nums.size() - 1; i >= 1; -- i){
if(nums[i] >= nums[i - 1]) break;
swap(nums[i], nums[i-1]);
}
}
double findMedian() {
int mid = nums.size() / 2;
if(nums.size() % 2 == 1)
return 1.0 * nums[mid];
return 1.0 * (nums[mid] + nums[mid - 1]) / 2;
}
private:
vector<int> nums;
};
2、中位数为根的BST
如果我们使用二分查找,找到新加入元素的位置,是否可行呢?答案是可行的,但是使用数组存储并不能很快更新。
- 使用高效率的树形二分查找,查找和插入效率很高,可以使用AVL、红黑树、B树等
- 但这里要求的是能快速取得中位数,普通的树形二分查找就不行了,不能通过下标快速找到。因此只能使用数组二分查找,但是插入效率又不高
根据上面的讨论,我们发现,如果能每次插入维护的一个二叉搜索树是一个完全二叉树,根附近就是中位数,并且插入操作只需要 O ( l o g n ) O(logn) O(logn)的时间,那就太好了。
这样我们就可以思考,能不能实现这样的数据结构:
- 对于任何一段区间,满足根是中位数,且左子树小于根,根小于右子树的一个二叉搜索树
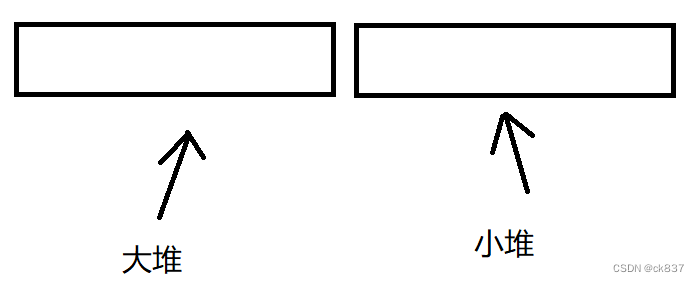
- 我们规定偶数情况下,两个数小者作为根。如下图:

- 我们规定偶数情况下,两个数小者作为根。如下图:
如果能实现这样的数据结构,就刚好和题目要求实现“数据结构”这一说法匹配了!
(我感觉是能实现的,但是时间问题,我就先不写了,有兴趣的同学可以自行研究)
3、优先队列
维护两个优先队列,一个存储比中位数小于的最大堆,一个存储比中位数大的最小堆(包括等于的,即最小堆里面的元素可能会比最大堆多一个)。那么我们就将数分为了两堆,很显然中位数能通过某种方式从两个优先队列队头取到。
并且很显然,维护这两个堆也很容易,当需要插入一个数时,我们只需要比较两个堆队头就可以选择插入的堆。并且为了维持两个堆队头是中位数
- 当元素数为偶数时,插入一个元素,如果插入到左边,则最后中位数会出现在左边,我们将其放入右边。如果插入到右边则直接结束
- 当元素数为奇数,插入一个元素,如果插入到左边则结束,如果插入到右边则右边多一个需要放一个放到左边。
- 不管怎么放,根据优先队列的性质,队头都是最值,即根据中位数将区间分为两段,通过优先队列快速进行维护,左右的边界值。
时间复杂度:
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn),一次插入时间复杂度
O
(
l
o
g
n
)
O(logn)
O(logn)
空间复杂度:
O
(
n
)
O(n)
O(n)

class MedianFinder {
public:
MedianFinder() {left.push(-0x3f3f3f3f);right.push(0x3f3f3f3f);}
void addNum(int num) {
++n;
//先插入
if(num >= right.top()){
right.push(num);
}else left.push(num);
//再移动
if(left.size() > right.size()){
right.push(left.top());
left.pop();
}else{
if(right.size() == left.size() + 2){
left.push(right.top());
right.pop();
}
}
return;
}
double findMedian() {
if(n & 1){//n & 1 == 1 即奇数
return right.top();
}
return (left.top() + right.top()) / 2.0;
}
private:
priority_queue<int, vector<int>, less<int>> left;//左区间
priority_queue<int, vector<int>, greater<int>> right;//右区间
int n = 0;
};




![[第五空间 2021]WebFTP、[HCTF 2018]Warmup](https://img-blog.csdnimg.cn/direct/2f7534d5deef4261aa6b0a45e5b9dbdc.png)