​​​​​​​​​​

一、思路

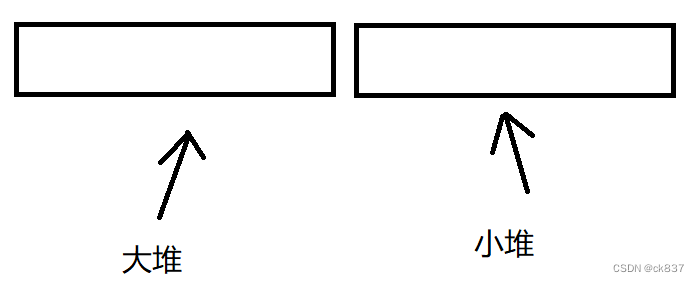
我们将所有数据平分成两份，前面那一部分用小堆来存，后面的部分用大堆来存，这样我们就能立刻拿到中间位置的值。

如果是奇数个数字，那么我们就将把中间值放在前面的大堆里，所以会有两种情况，我们将大堆成为left，小堆成为right。

• 当数据量是偶数的时候，left.size() == right.size()，这时候中间值就是left.top()
• 当数据量是奇数的时候，这时候的left.size() == right.size() + 1，这时候的中位数就是 (left.size() + right.size()) / 2.0

二、如何存储数据？

因为左边是大堆，右边是小堆，这时候会有两个大类的情况

第一种 left.size() = right.size()

这时候，由于左边的数据都是会比left.top()小，右边的数据都会比左边的数据大，所以我们可以根据这个条件开进行讨论
假如要插入的数据是num

• 如果left.empty() || num <= left.top() ，这时候就直接将num插进左边的大堆中
• 如果num > left.top()，这时候应该要插进右边的小堆，但由于我们规定只能两边数据相等，或者右边的比左边的数据量多一个，所以这时候我们要：
  1.先把数据插入进right，
  2.然后拿到right.top(),因为这是right的最小值
  3.将right.top() 插进 left.top()中，然后再让right.pop()

第二种 left.size() > right.size()

• 如果num > left.top() ，直接把num插进right中
• 如果num <= left.top()， 这时候由于left的大小比right多1，所以我们可以参考第一种情况那样

1. 把数据插进left
2. 将left.top() 插入到 right中
3. left.pop()

三、代码

class MedianFinder {
public:
    priority_queue<int> left;
    priority_queue<int, vector<int>, greater<int>> right;
    MedianFinder() {

    }
    
    void addNum(int num) {
        if(left.size() == right.size())
        {
            if(left.empty() || left.top() >= num) 
            {
            	left.push(num);
            }
            else if(left.top() < num)   
            {
                right.push(num);
                int y = right.top();
                right.pop();
                left.push(y);
            }
        }
        else
        {
            if(left.top() >= num)   
            {
                left.push(num);
                right.push(left.top());
                left.pop();
            }
            else 
            {
                right.push(num);
            }
        }
        
    }
    
    double findMedian() {
        if(left.size() == right.size()) return (left.top() + right.top()) / 2.0;
        else return left.top();
    }
};