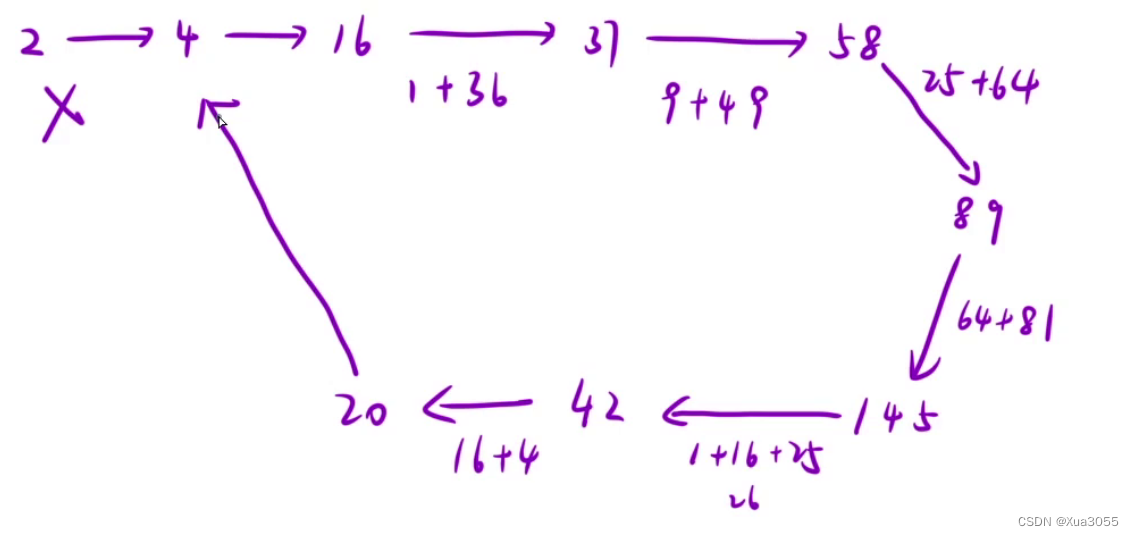
回溯基础理论
1.回溯的本质是利用递归进行暴力搜索,将符和条件的结果集搜索出来
2.回溯法常见的问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 棋盘问题:N皇后,解数独等等
3.回溯法常见模板
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}4.回溯法抽象为一个图形来理解就容易多了,在后面的每一道回溯法的题目我都将遍历过程抽象为树形结构,利用树形结构可以形象化回溯的过程,便于理解,所以在解决回溯问题时,可以将二叉搜索树画出来
复习题1
77. 组合 - 力扣(LeetCode)
二叉搜索你树

回溯三部曲:
1.确认递归返回值及参数
public List<List<Integer>> res = new ArrayList<>();
public List<Integer> list = new ArrayList<>();res用于收集最后所有可能的结果,list用于存储符合条件的单一结果
2.回溯终止条件
当list的大小为k时既符合题目条件
if (list.size() == k) {
res.add(new ArrayList<>(list));
return;
}3.单层搜索的过程、
从startindex开始进行遍历,将符合条件的数加入到list中后继续向下递归
for循环每次从startIndex开始遍历,然后用list保存取到的节点i。
for (int i = start; i <= n - (k - list.size()) + 1; i++) {
list.add(i);
dfs(k, n, i + 1);
list.remove(list.size() - 1);
}完整代码:
class Solution {
public List<List<Integer>> res = new ArrayList<>();
public List<Integer> list = new ArrayList<>();
public void dfs(int k, int n, int start) {
if (list.size() == k) {
res.add(new ArrayList<>(list));
return;
}
for (int i = start; i <= n - (k - list.size()) + 1; i++) {
list.add(i);
dfs(k, n, i + 1);
list.remove(list.size() - 1);
}
return;
}
public List<List<Integer>> combine(int n, int k) {
dfs(k,n,1);
return res;
}
}复习题2
216. 组合总和 III - 力扣(LeetCode)
二叉搜索树

本体与上题的搜索过程是像相同的,在条件上加了一个和为指定数
回溯三部曲
1.确认递归返回值及参数
public List<List<Integer>> res = new ArrayList<>();
public List<Integer> list = new ArrayList<>();res用于收集最后所有可能的结果,list用于存储符合条件的单一结果
2.回溯终止条件
当list的大小为k,并且和为n时既符合题目条件,或者当前list中元素的和已经大于n时也没有继续搜索的必要了
if(sum>n){
return;
}
if (list.size() == k&&sum==n) {
res.add(new ArrayList<>(list));
return;
}3.单层搜索过程
从startindex开始进行遍历,将符合条件的数加入到list中后,sum对其相加后 继续向下递归,回溯时将list最后的数移除,sum进行相减
for循环每次从startIndex开始遍历,然后用list保存取到的节点i。
for (int i = start; i <= 9; i++) {
sum += i;// 处理
list.add(i);
dfs(n, k, i + 1, sum);// 向下搜
sum -= i;// 回溯
list.remove(list.size() - 1);
}完整代码:
class Solution {
public List<List<Integer>> res = new ArrayList<>();
public List<Integer> list = new ArrayList<>();
public void dfs(int n, int k, int start, int sum) {
if (sum > n) {
return;// (如果sum>n那么后面在加就没有意义了)剪枝
}
if (list.size() == k && sum == n) {
res.add(new ArrayList<>(list));// 收集结果
return;
}
for (int i = start; i <= 9; i++) {
sum += i;// 处理
list.add(i);
dfs(n, k, i + 1, sum);// 向下搜
sum -= i;// 回溯
list.remove(list.size() - 1);
}
return;
}
public List<List<Integer>> combinationSum3(int k, int n) {
int sum = 0;
dfs(n, k, 1, sum);
return res;
}
}复习题3
216. 组合总和 III - 力扣(LeetCode)
二叉搜索树

本题的不同点在于数组中的元素可以多次使用,所以在下次递归时的startIndex不用加一还是从当前元素开始
回溯三部曲
1.确认递归返回值及参数
public List<List<Integer>> res = new ArrayList<>();
public List<Integer> list = new ArrayList<>();res用于收集最后所有可能的结果,list用于存储符合条件的单一结果
2.递归终止条件
当list的元素的和为targetSum时既符合题目条件或者当sum大于targetSum时也没有继续搜索的必要了
//sum>=target就返回
if (sum > target) {
return;
}
if (sum == target) {
res.add(new ArrayList<>(list));
return;
}
3.单层搜索过程
从startIndex开始对nums数组进行遍历将nums数组的元素加入到list中后进行向下递归,注意下次的开始位置任然为当前元素位置(本题的元素可以重复选)
for (int i = start; i < nums.length; i++) {
list.add(nums[i]);//处理
sum += nums[i];
dfs(nums, target, i);//递归,注意这里是i(表示可以重复读取当前的数)
list.remove(list.size() - 1);//回溯
sum -= nums[i];
}完整代码:
class Solution {
public List<List<Integer>> res = new ArrayList<>();
public List<Integer> list = new ArrayList<>();
public int sum = 0;
/**
* @param nums 目标数组
* @param target 目标和
* @param start 起始位置
*/
public void dfs(int[] nums, int target, int start) {
//sum>=target就返回
if (sum > target) {
return;
}
if (sum == target) {
res.add(new ArrayList<>(list));
return;
}
for (int i = start; i < nums.length; i++) {
list.add(nums[i]);//处理
sum += nums[i];
dfs(nums, target, i);//递归,注意这里是i(表示可以重复读取当前的数)
list.remove(list.size() - 1);//回溯
sum -= nums[i];
}
}
public List<List<Integer>> combinationSum(int[] candidates, int target) {
dfs(candidates, target, 0);
return res;
}
}复习题4
40. 组合总和 II - 力扣(LeetCode)
二叉搜索树
本题较上题元素不能重复使用,并且数组中存在重复元素需要考虑去重的问题(利用set将选过的数进行保存,在遍历前判断是否存在来避免重复选择相同的元素,使用前提需要对数组进行排序,为了将相同元素放到一起)
回溯三步曲:
1.确认递归返回值及参数
public List<List<Integer>> res = new ArrayList<>();
public List<Integer> list = new ArrayList<>();res用于收集最后所有可能的结果,list用于存储符合条件的单一结果
2.递归终止条件
当list的元素的和为targetSum时既符合题目条件或者当sum大于targetSum时也没有继续搜索的必要了
//sum>=target就返回
if (sum > target) {
return;
}
if (sum == target) {
res.add(new ArrayList<>(list));
return;
}
3.单层搜索过程从startIndex进行搜索,将数组中的数加入,后向下递归回溯
HashSet<Integer> set = new HashSet<>();
for (int i = startIndex; i <nums.length ; i++) {
if(set.contains(nums[i])){
continue;
}
set.add(nums[i]);
list.add(nums[i]);
sum+=nums[i];
dfs(nums,targetSum,sum,i+1);
sum-=nums[i];
list.remove(list.size()-1);
}完整代码:
public static List<List<Integer>> res = new ArrayList<>();
public static List<Integer> list = new ArrayList<>();
/**
*/
public static void dfs(int[]nums,int targetSum,int sum,int startIndex) {
if(sum>targetSum){
return;
}
if(sum==targetSum){
res.add(new ArrayList<>(list));
return;
}
HashSet<Integer> set = new HashSet<>();
for (int i = startIndex; i <nums.length ; i++) {
if(set.contains(nums[i])){
continue;
}
set.add(nums[i]);
list.add(nums[i]);
sum+=nums[i];
dfs(nums,targetSum,sum,i+1);
sum-=nums[i];
list.remove(list.size()-1);
}
}
public static List<List<Integer>> f(int []nums, int targetSum) {
Arrays.sort(nums);
dfs(nums,targetSum,0,0);
return res;
}复习题5
多个集合求组合
17. 电话号码的字母组合 - 力扣(LeetCode)
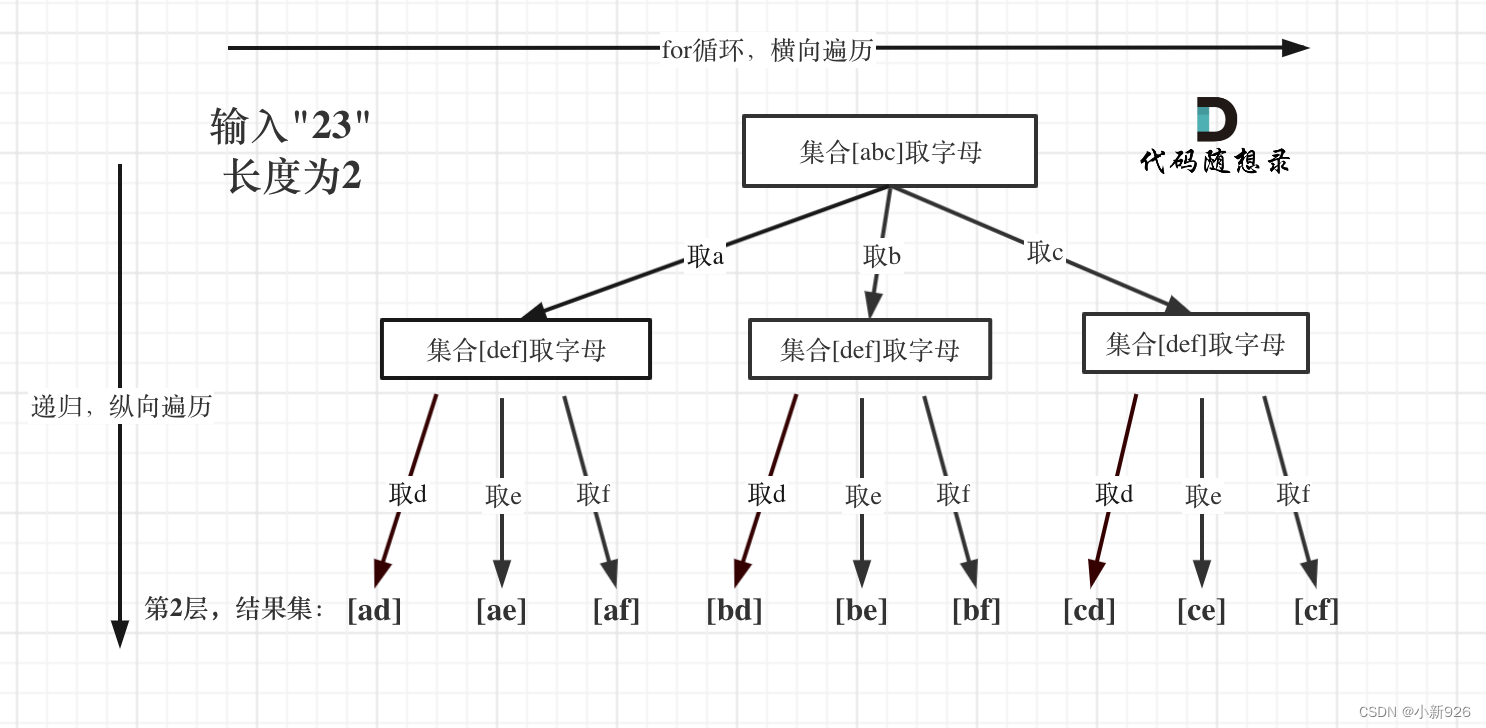
数字和字母如何映射
利用map将数字和字符进行映射
public void f(String digits) {
map.put(2, "abc");
map.put(3, "def");
map.put(4, "ghi");
map.put(5, "jkl");
map.put(6, "mno");
map.put(7, "pqrs");
map.put(8, "tuv");
map.put(9, "wxyz");
}回溯三部曲
1.确认参数和返回值
res用于存储最终答案,ans用于存储单一搜索答案
public List<String> res = new ArrayList<>();
public StringBuilder ans = new StringBuilder();利用len表示当前res的长度,key表示当前遍历的数字
2.递归终止条件
如题可知当res的长度等于digits时递归终止
if(len==digits.length()){//收集结果
res.add(ans.toString());
return;
}
3.单一搜索过程
对digits进行遍历后对向下一个数字对应的字符进行递归
String str=map.get(digits.charAt(key)-'0');//获取当前需要操作的字符串,如“23”,即先2,3
for (int i =0; i <str.length() ; i++) {
ans.append(str.charAt(i));//处理
dfs(digits,map,len+1,key+1);//向下搜
ans.delete(ans.length()-1,ans.length());//回溯
}完整代码:
class Solution {
public HashMap<Integer, String> map = new HashMap<>();
public List<String> res = new ArrayList<>();
public StringBuilder ans = new StringBuilder();
public void f(String digits) {
map.put(2, "abc");
map.put(3, "def");
map.put(4, "ghi");
map.put(5, "jkl");
map.put(6, "mno");
map.put(7, "pqrs");
map.put(8, "tuv");
map.put(9, "wxyz");
}
/**
*
* @param digits 目标参数
* @param map 映射map
* @param num 当前操作的字符串在map中对应的key,
* @param len 当前字符ans的长度
*/
public void dfs(String digits,HashMap<Integer,String> map,int len,int key ){
f(digits);
if(len==digits.length()){//收集结果
res.add(ans.toString());
return;
}
String str=map.get(digits.charAt(key)-'0');//获取当前需要操作的字符串,如“23”,即先2,3
for (int i =0; i <str.length() ; i++) {
ans.append(str.charAt(i));//处理
dfs(digits,map,len+1,key+1);//向下搜
ans.delete(ans.length()-1,ans.length());//回溯
}
}
public List<String> letterCombinations(String digits) {
if(digits==null||digits.length()==0){
return res;
}
dfs(digits, map, 0,0);
return res;
}
}复习题6
切割问题
131. 分割回文串 - 力扣(LeetCode)

切割问题依然可以抽象成组合问题
递归用来纵向遍历,for循环用来横向遍历,切割线(就是图中的红线)切割到字符串的结尾位置,说明找到了一个切割方法。
判断回文
public boolean cheak(String s,int start,int end){
for (int i = start,j=end; i <j ; i++,j--) {
if(s.charAt(i)!=s.charAt(j)){
return false;
}
}
return true;
}本题注意 利用startIndex代表分割线当startIndex大于了是s.length()也就到达了叶子节点、
完整代码:
class Solution {
public List<List<String>> res=new ArrayList<>();
public List<String> list=new ArrayList<>();
public boolean cheak(String s,int start,int end){
for (int i = start,j=end; i <j ; i++,j--) {
if(s.charAt(i)!=s.charAt(j)){
return false;
}
}
return true;
}
public void dfs(String s,int startIndex) {
if (startIndex >= s.length()) {
res.add(new ArrayList(list));
return;
}
for (int i = startIndex; i < s.length(); i++) {
//如果是回文子串,则记录
if (cheak(s, startIndex, i)) {
String str = s.substring(startIndex, i + 1);
list.add(str);
} else {
continue;
}
//起始位置后移,保证不重复
dfs(s, i + 1);
list.remove(list.size() - 1);
}
}
public List<List<String>> partition(String s) {
dfs(s, 0);
return res;
}
}复习题7
子集问题
78. 子集 - 力扣(LeetCode)
子集问题与组合问题不同的是对所有的叶子节点都需要搜集,所以在搜集答案时不需要return 了
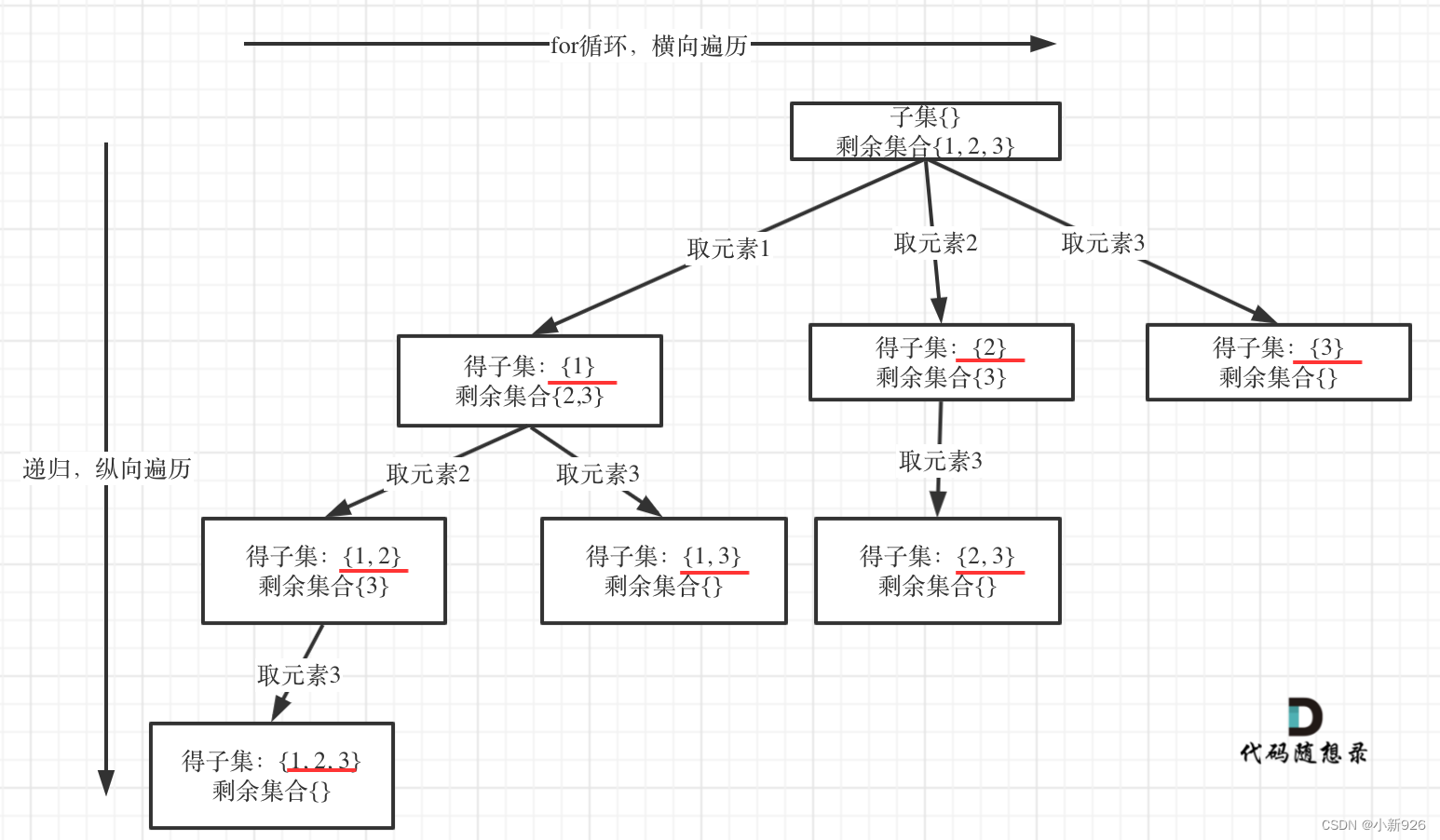
本题其实可以不需要加终止条件,因为startIndex >= nums.size(),本层for循环本来也结束了,本来我们就要遍历整棵树。
有的同学可能担心不写终止条件会不会无限递归?
并不会,因为每次递归的下一层就是从i+1开始的。
如果要写终止条件,注意:result.push_back(path);要放在终止条件的上面,如下:
result.push_back(path); // 收集子集,要放在终止添加的上面,否则会漏掉结果
if (startIndex >= nums.size()) { // 终止条件可以不加
return;
}完整代码:
class Solution {
public List<List<Integer>> res=new ArrayList<>();
public List<Integer> list=new ArrayList<>();
public void dfs(int []nums,int startIndex){
res.add(new ArrayList<>(list));
for (int i = startIndex; i <nums.length ; i++) {
list.add(nums[i]);
dfs(nums,i+1);
list.remove(list.size()-1);
}
}
public List<List<Integer>> subsets(int[] nums) {
dfs(nums,0);
return res;
}
}在回溯算法:求子集问题(二) (opens new window)中,开始针对子集问题进行去重。
class Solution {
public List<List<Integer>> res=new ArrayList<>();
public List<Integer> list=new ArrayList<>();
public void dfs(int []nums,int startIndex){
res.add(new ArrayList<>(list));
for (int i = startIndex; i <nums.length ; i++) {
if(i>startIndex&&nums[i]==nums[i-1]){
continue;
}
list.add(nums[i]);
dfs(nums,i+1);
list.remove(list.size()-1);
}
}
public List<List<Integer>> subsetsWithDup(int[] nums) {
Arrays.sort(nums);
dfs(nums,0);
return res;
}
}复习题8
排列问题
46. 全排列 - 力扣(LeetCode)
排列问题与祝贺问题不同的是排列问题与与顺序有关如[1,2]和[2,1]是相同的组合但是是不同的排列
那么可能前面选了2后面可能选1 也就说明每次都从0开始,然后需要used数组对已经选过的数进行保存
完整代码:
class Solution {
public List<List<Integer>> res = new ArrayList<>();
public List<Integer> list = new ArrayList<>();
public boolean[] isUse = new boolean[10];
/**
* @param nums 数组
* @param x 当前放数的位置
*/
public void dfs(int[] nums, int x) {
if (x == nums.length) {
res.add(new ArrayList<>(list));
return;
}
for (int i = 0; i < nums.length; i++) {
if (!isUse[i]) {
isUse[i] = true;
list.add(nums[i]);
dfs(nums, x + 1);
isUse[i] = false;
list.remove(list.size() - 1);
}
}
}
public List<List<Integer>> permute(int[] nums) {
dfs(nums, 0);
return res;
}
}47. 全排列 II - 力扣(LeetCode)
在此题基础上增加去重过程即可
class Solution {
public List<List<Integer>> res = new ArrayList<>();
public List<Integer> list = new ArrayList<>();
public boolean[] isUse = new boolean[10];
/**
* @param nums 数组
* @param x 当前放数的位置
*/
public void dfs(int[] nums, int x) {
if (x == nums.length) {
res.add(new ArrayList<>(list));
return;
}
HashSet<Integer> set = new HashSet<>();
for (int i = 0; i < nums.length; i++) {
if(set.contains(nums[i])){//对同层选过的节点进行去重
continue;
}
if (!isUse[i]) {
isUse[i] = true;
list.add(nums[i]);
set.add(nums[i]);
dfs(nums, x + 1);
isUse[i] = false;
list.remove(list.size() - 1);
}
}
}
public List<List<Integer>> permuteUnique(int[] nums) {
dfs(nums, 0);
return res;
}
}关于去重
去重问题
以上我都是统一使用used数组来去重的,其实使用set也可以用来去重!
在本周小结!(回溯算法系列三)续集 (opens new window)中给出了子集、组合、排列问题使用set来去重的解法以及具体代码,并纠正一些同学的常见错误写法。
同时详细分析了 使用used数组去重 和 使用set去重 两种写法的性能差异:
使用set去重的版本相对于used数组的版本效率都要低很多,大家在leetcode上提交,能明显发现。
原因在回溯算法:递增子序列 (opens new window)中也分析过,主要是因为程序运行的时候对unordered_set 频繁的insert,unordered_set需要做哈希映射(也就是把key通过hash function映射为唯一的哈希值)相对费时间,而且insert的时候其底层的符号表也要做相应的扩充,也是费时的。
而使用used数组在时间复杂度上几乎没有额外负担!
使用set去重,不仅时间复杂度高了,空间复杂度也高了,在本周小结!(回溯算法系列三) (opens new window)中分析过,组合,子集,排列问题的空间复杂度都是O(n),但如果使用set去重,空间复杂度就变成了O(n^2),因为每一层递归都有一个set集合,系统栈空间是n,每一个空间都有set集合。
那有同学可能疑惑 用used数组也是占用O(n)的空间啊?
used数组可是全局变量,每层与每层之间公用一个used数组,所以空间复杂度是O(n + n),最终空间复杂度还是O(n)。