【递归、搜索与回溯】搜索

news2024/10/7 0:04:07

搜索

  • 1.计算布尔二叉树的值
  • 2.求根节点到叶节点数字之和
  • 3. 二叉树剪枝
  • 4.验证二叉搜索树
  • 5.二叉搜索树中第K小的元素
  • 6.二叉树的所有路径

在这里插入图片描述

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励，我们一起努力吧!😃😃

1.计算布尔二叉树的值

题目链接：2331. 计算布尔二叉树的值

题目分析：

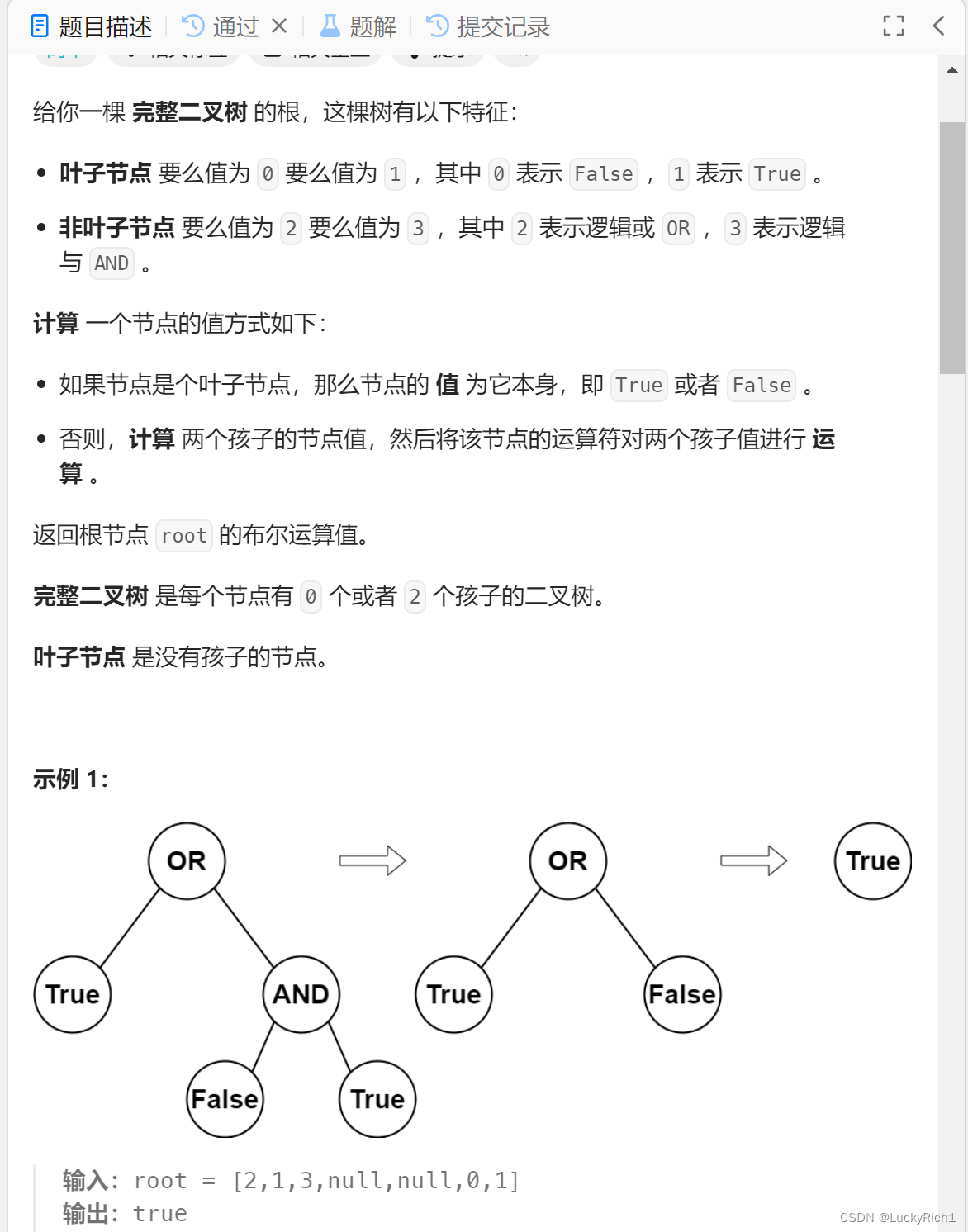
在这里插入图片描述

给一颗完整二叉树，孩子节点要么是0要么是2，不存在1个孩子节点。
叶子节点和非叶子节点数字分别代表不同的意思，最后将root根结果bool值返回去。

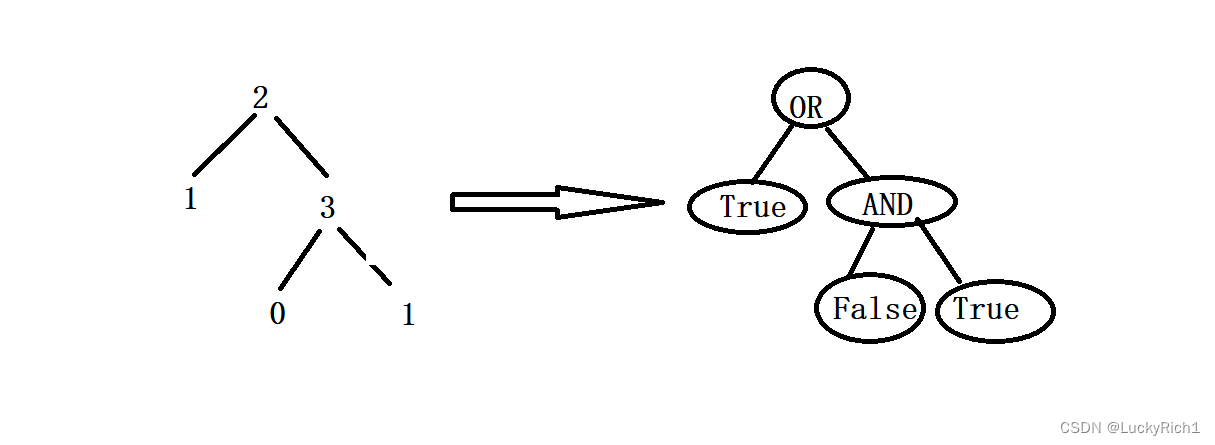
在这里插入图片描述
算法原理：

解法：递归
宏观角度看待递归
当想知道root根节点bool值时，我要先知道左子树bool值，在知道右子树bool值，然后将左右子数的bool值和root本身信息做整合。当我们要知道左子树和右子树的bool值，你会发现它和大问题是一样的。大问题是解决整棵树的bool值，小问题是解决左子树bool值，右子树bool值。此时把左指针传给dfs，dfs把左子树bool值给你，把右指针传给dfs，dfs把右子树bool值给你。所以dfs非常好设计。
函数头
bool dfs(TreeNode* root)

在这里插入图片描述
函数体也就出来了，先求左子树bool值，在求右子树bool，不要管递归如何执行，只需要知道你给它数据它一定能完成任务。
bool left=dfs(root->left)
bool right=dfs(root->right)
最后在将左子树和右子树bool值和root做整合。

递归出口 到叶子节点就不需要往后递归了，此时返回结果就行了

class Solution {
public:
    bool evaluateTree(TreeNode* root) {
        
        if(root->left == nullptr) return root->val == 0 ? false : true;

        bool left=evaluateTree(root->left);
        bool right=evaluateTree(root->right);

        return root->val == 2 ? left|right : left&right;
        
    }
};

2.求根节点到叶节点数字之和

题目链接：129. 求根节点到叶节点数字之和

题目分析：

在这里插入图片描述

将根到叶子节点组合的数加起来

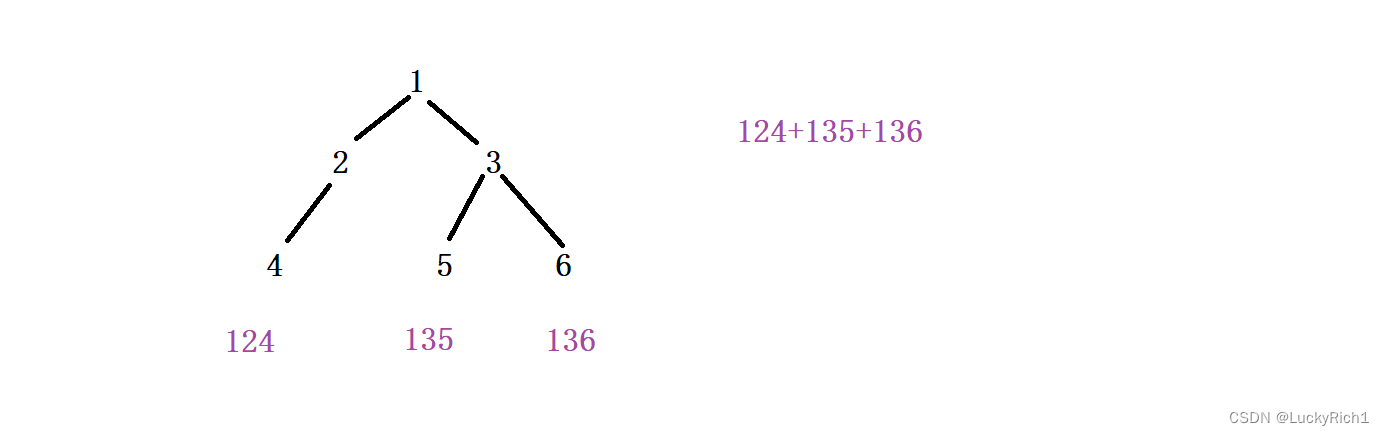
在这里插入图片描述

算法原理：

解法：递归
首先我们要找到相同子问题，在树中相同子问题很好找，只需要关注递归到每一层需要干什么事情即可。当它们干的都是一样的事情，这就是相同的子问题。

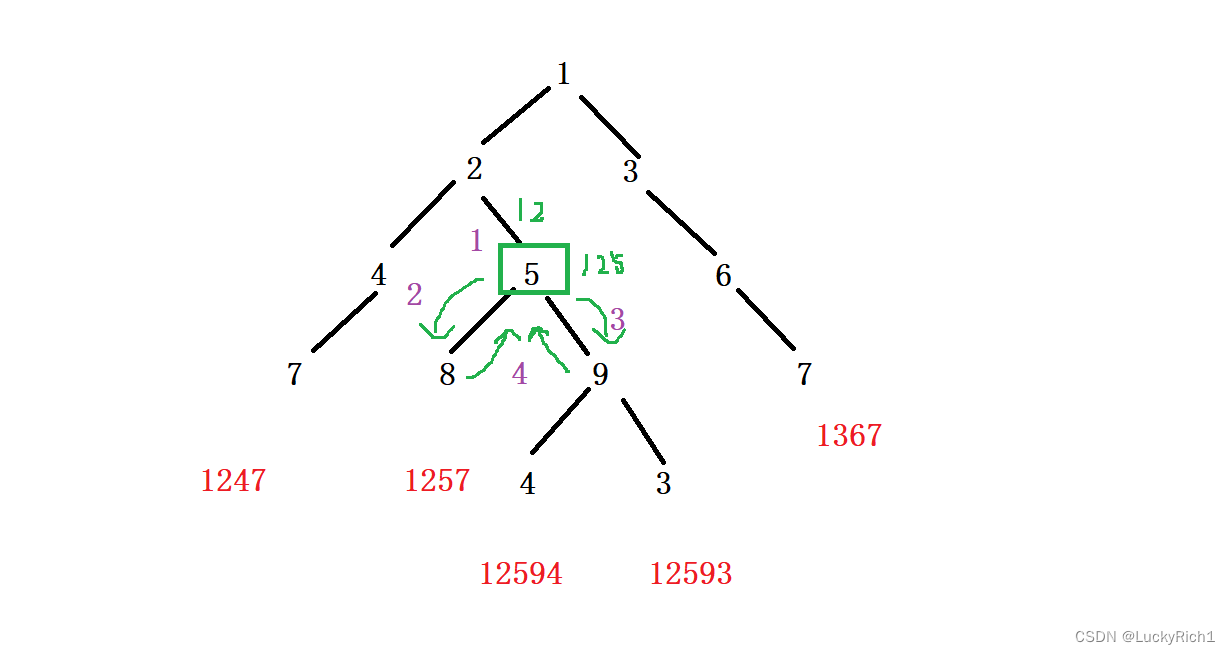
当递归到5这一层，我发现要拿到和5相连下面的叶子节点的数把它们加起来，然后返回给根节点。当到5这一层

  1. 首先要把12先给我传过来，不然我怎么算出1258，也就是到某一层要把它之前路径上之后给我传过来。然后拿到这个12，先算出125。
  2. 然后把125传给左边
  3. 把125传给右边
  4. 然后把左边值的和与右边值的和相加，然后返回上一层节点

在这5这一层要完成4个任务，同理其他层也是要完成相同的任务。

在这里插入图片描述

1.函数头
首先要有一个返回值，就是传给dfs一个根节点把和它相连的叶子节点的和返回。但是要注意的是，我们除了要传一个根节点，还需要再把递归到该层的上面路径和拿到！ 因此函数头是int dfs(root，presum)

2.函数体
1、2、3、4个步骤

3.递归出口
当到叶子节点就可以返回了，但是要注意的是，这个递归出应该在步骤1之后的，因为到叶子节点也要把叶子节点的数加上才向上返回的。

class Solution {
public:
    int sumNumbers(TreeNode* root) {
        
        return dfs(root,0);

    }

    int dfs(TreeNode* root,int presum)
    {
        presum=presum*10+root->val;

        if(root->left == nullptr && root->right == nullptr)
            return presum;
          
        int ret=0;
        if(root->left) ret+=dfs(root->left,presum);
        if(root->right) ret+=dfs(root->right,presum);

        return ret;

    }
};

3. 二叉树剪枝

题目链接：814. 二叉树剪枝

题目分析：

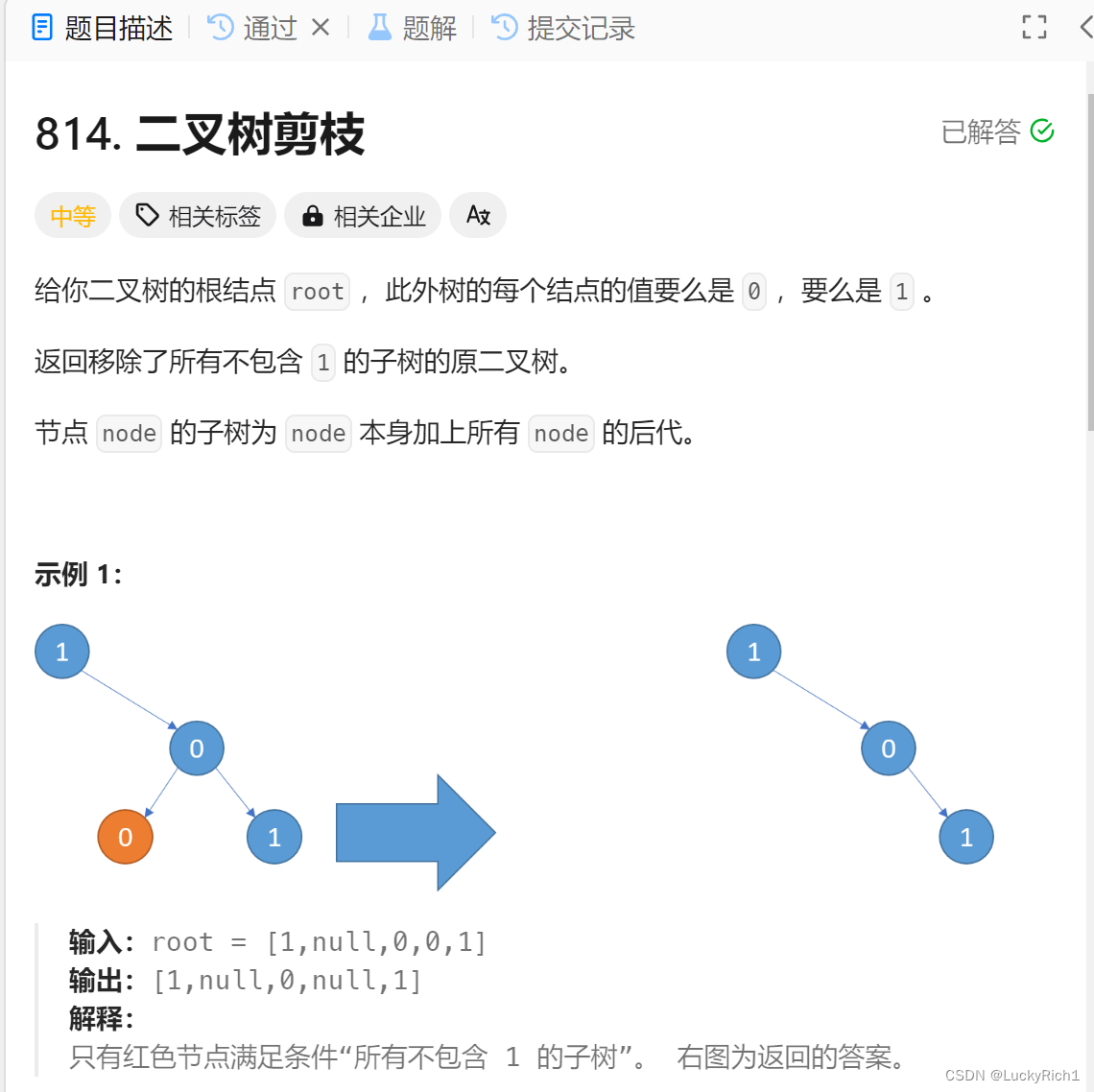
在这里插入图片描述

注意这里的剪枝和前面说的剪枝是不一样的，前面的是那条路不是通往终点的路不能在走了，这里的剪枝真的就是把分枝剪掉！

返回移除了所有 不包含 1 的子树 的原二叉树 的意思是，就是如果子树全是0就把它剪掉。如果子数既有1又有0就不能剪掉。
在这里插入图片描述

算法原理：

通过决策树，抽象出递归的三个核心问题
也就是说通过，完成二叉树剪枝这个任务，完成递归三个核心问题。
像之前先把每个子问题要完成任务先找到，但是有时候某些道题非常麻烦，无法总结出子问题到底干了什么问题，这道题是给一个根节点然后把子树全为0剪掉然后把新根节点返回来。但是有些题特别抽象你根本无法总结出来你让这个递归去完成什么任务，任务太多了。此时我们要有一个能力，通过研究递归的过程来总结出函数头、函数体、递归出口！

在这里插入图片描述

首先这肯定是一个后序遍历，先要确定左右子树是什么情况才能决定是否把这个子树干掉。

当作后序遍历到底最左节点，然后再后序发现它左为空右为空，然后自己本身也是0，说明可以给它剪枝。然后回到上一层但是有一个问题，是不是要修改上一层左子树的指针啊，因此这个递归函数要有一个返回值 TreeeNode*。
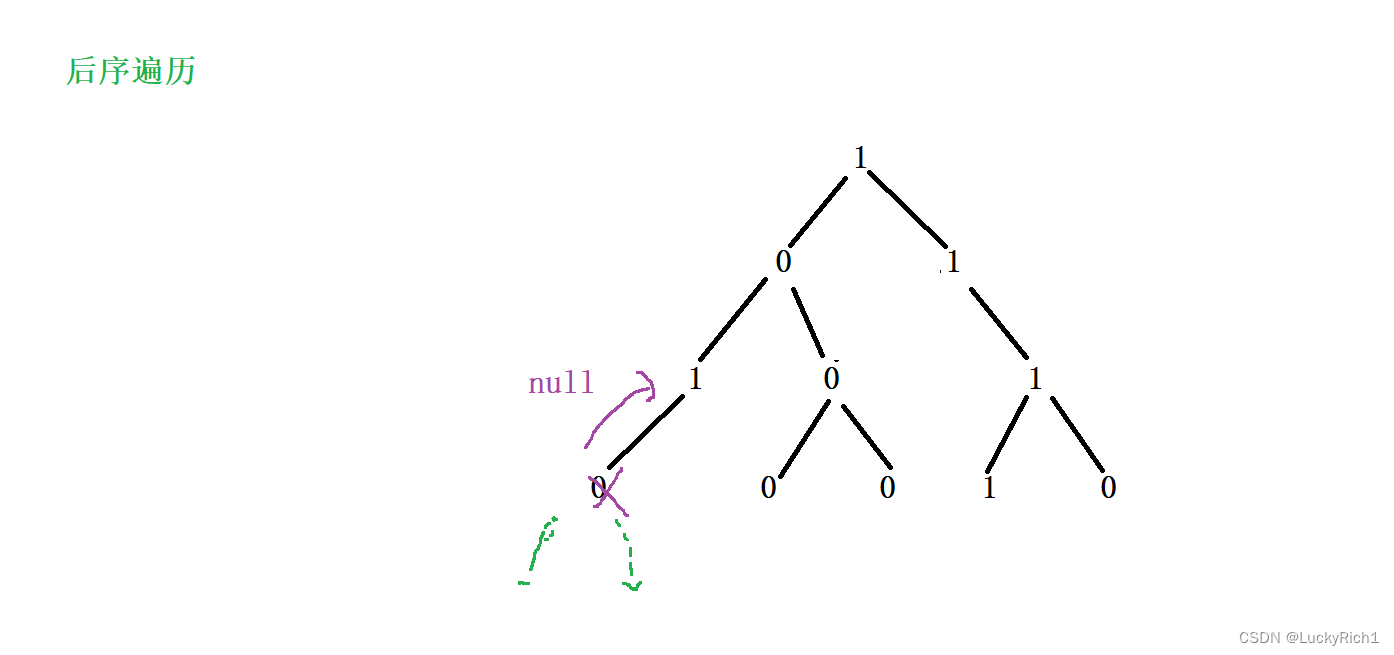
在这里插入图片描述
然后如果左右子树都为空，但自己是1，说明不能剪枝
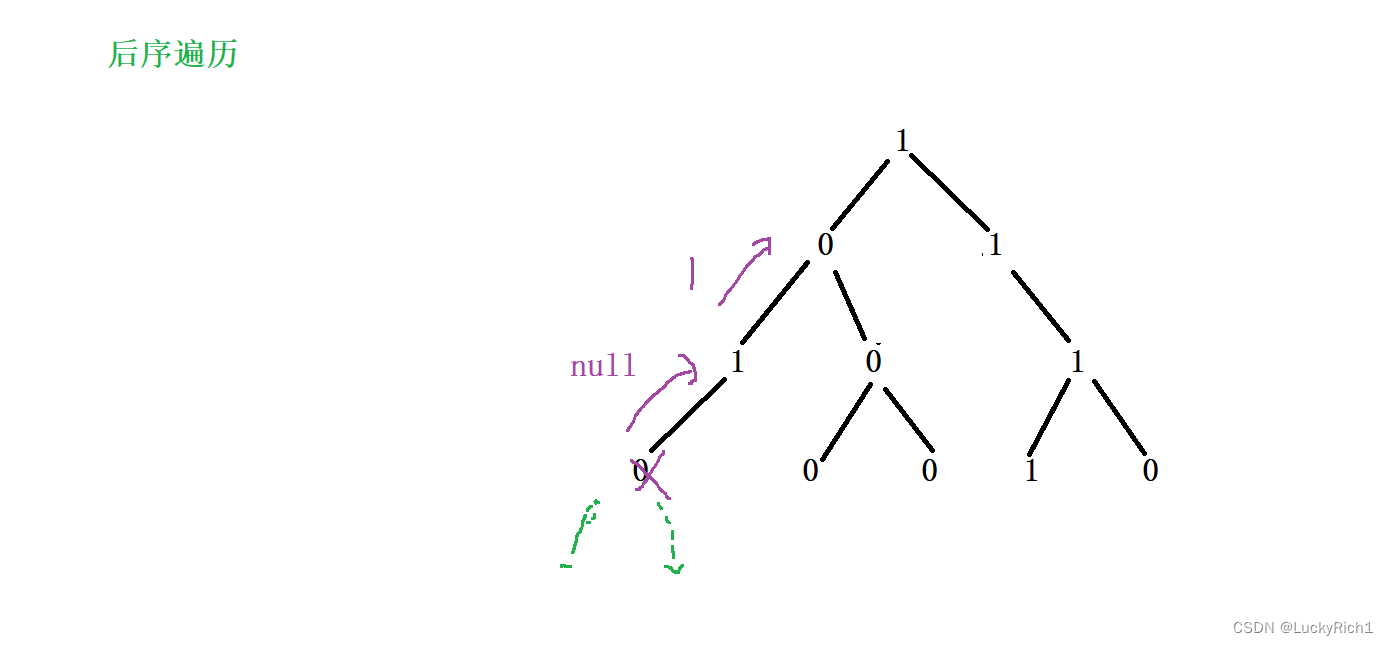
在这里插入图片描述
当我们把根左子树都弄好了，其实整个递归过程就出来。
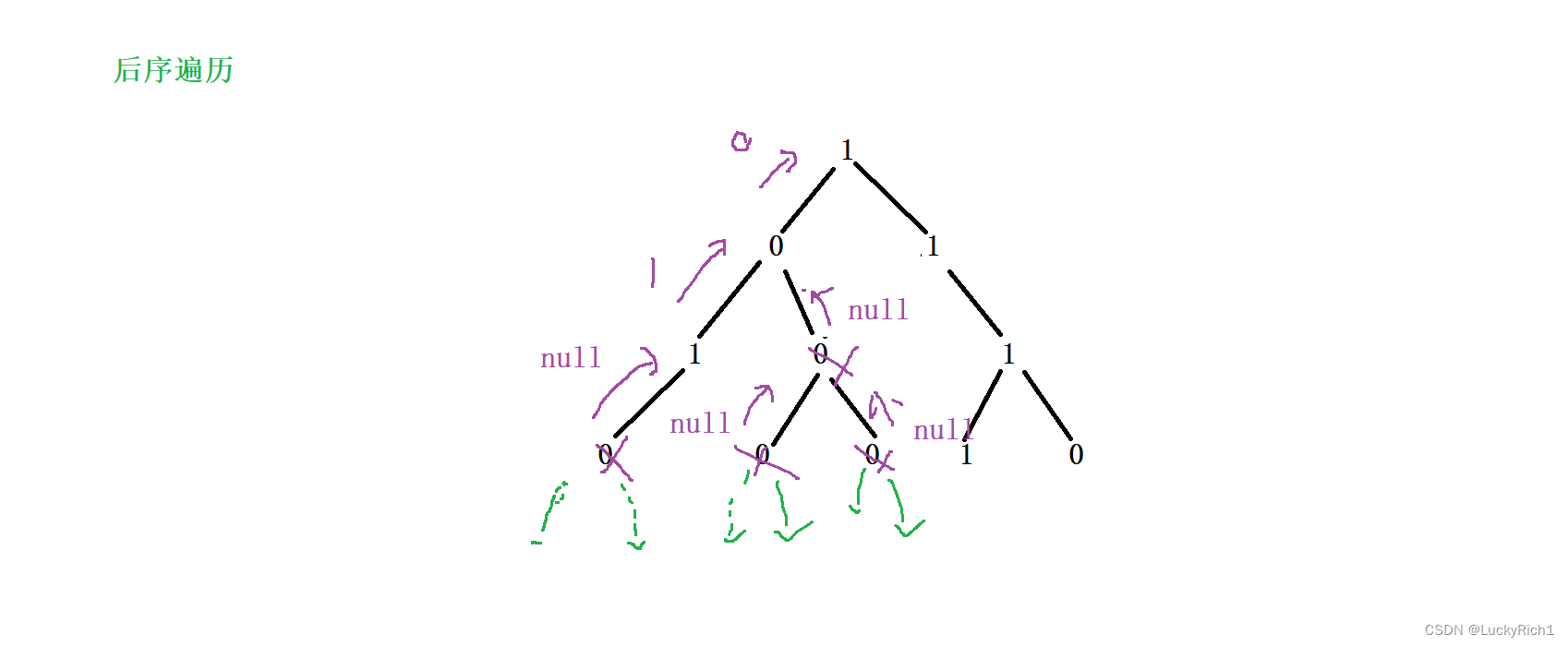
在这里插入图片描述

  1. 函数头
    TreeNode* dfs(root) 给一个根节点，然后把结果给我
  2. 函数体
    左子树右子树都搞完返回给我一个东西，然后通过返回值在结合我自己看是否需要把自己删除。
    1.左子树、2.右子树、 3.判断
  3. 递归出口
    遇到null结束，就返回null
class Solution {
public:
    TreeNode* pruneTree(TreeNode* root) {

        if(root == nullptr) return nullptr;

        root->left=pruneTree(root->left);
        root->right=pruneTree(root->right);

        if(root->left == nullptr && root->right == nullptr && root->val == 0)
            return nullptr;
        else 
            return root;
        
    }
};

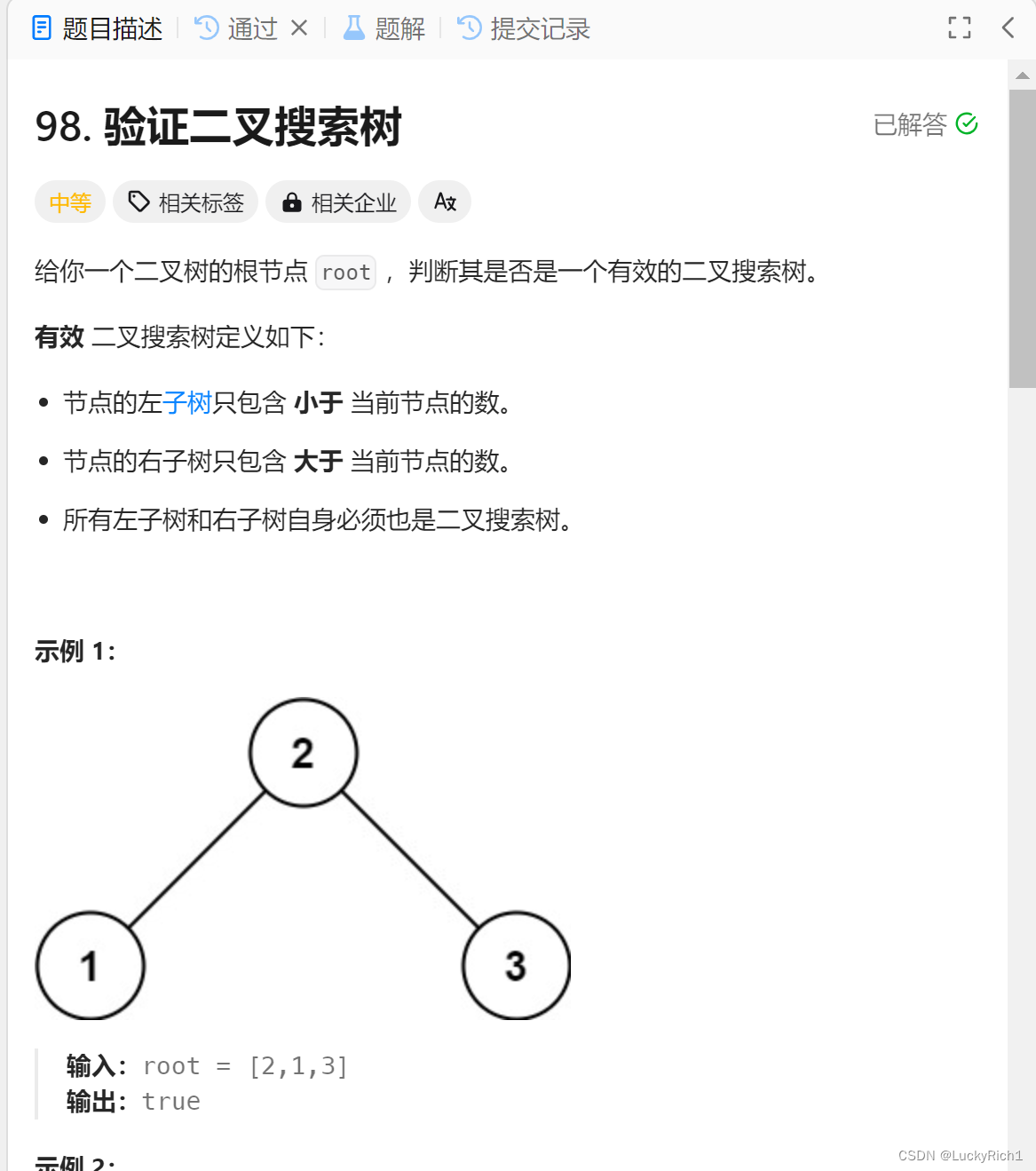
4.验证二叉搜索树

题目链接：98. 验证二叉搜索树

题目描述：

在这里插入图片描述

算法原理：
这道题主要想说的有三个方面 1. 全局变量的优势 ，2. 回溯 ，3. 剪枝

这里我们利用一个性质，二叉搜索树的中序遍历结果，是一个有序的序列
可能你会想到用一个数组记录中序遍历的结果，然后在遍历一下数组。但是这样空间开销太大了。

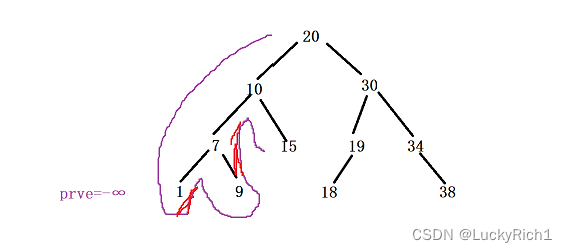
我们还是利用这个性质解决这个问题，但是我们可以仅用一个全局变量就来判断这个中序遍历是否是有序的。这个全局变量是在中序遍历中当我遍历到某一个位置它的前序是多少。 并且因为是全局的，并不需要考虑在递归中如何传递，直接拿过来用就可以了！
在这里插入图片描述

当中序遍历到第一个节点后，比较该值和prev的大小，当前这个值比无穷小大说明当前中序遍历是有序的，就更新prev等于这个值。然后向上传，同理依旧是拿这个值和prev做比较等等，知道中序遍历到19发现这个值比prev要小，此时中序遍历就不是有序的，说明30左子树就不一颗二叉搜索树，也说明20右子树不是一颗二叉搜索树，进而说明整棵树就不是一颗二叉搜索树。直接返回即可！

在这里插入图片描述

所以这道题我们可以借助全局变量和中序遍历就可以解决这个问题。
我们有两种策略判断它是否是一个二叉树。
策略一：

  1. 左子树是一颗二叉搜索树，
  2. 当前节点也要符合二叉搜索树的定义
  3. 右子树也是一颗二叉搜索树

此时就颗树就是一颗二叉搜索树！

一个递归99%都有回溯，往上层返回就是回溯！
在这里插入图片描述

当前节点值的范围正好有INT_MIN，如果我们prev=INT_MIN 有可能第一层判断就有问题。因此把prev类型换一下，long 或者 long long

在这里插入图片描述

class Solution {
public:
    long prev=LONG_MIN;
    bool isValidBST(TreeNode* root) {

        if(root == nullptr) return true;

        bool left=isValidBST(root->left);
        bool cur=false;
        if(root->val > prev)
        {
            prev=root->val;
            cur=true;
        }
        bool right=isValidBST(root->right);

        return left && cur && right;
    }
};

策略二：剪枝

当判断某棵子树不是二叉搜索树，整体就已经不是二叉搜索树了，就没有必要在去其他子树递归了，直接返回结果就行了。加快了我们的搜索过程
在这里插入图片描述
剪枝其实很简单，不要想的那么复杂。

class Solution {
public:
    long prev=LONG_MIN;
    bool isValidBST(TreeNode* root) {

        if(root == nullptr) return true;

        bool left=isValidBST(root->left);
        //剪枝
        if(left == false) return false;
        bool cur=false;
        if(root->val > prev)
        {
            prev=root->val;
            cur=true;
        }
        //剪枝
        if(cur == false) return false;
        bool right=isValidBST(root->right);

        return left && cur && right;
    }
};

5.二叉搜索树中第K小的元素

题目链接：230. 二叉搜索树中第K小的元素

题目描述：

在这里插入图片描述

算法原理：

有了上面题的基础，这道题就非常简单了，仅需两个全局变量+中序遍历就行了

每次count-1，直到count==0，用ret记录结果。找到最终结果此时其他子树也不用遍历。也可以使用剪枝。

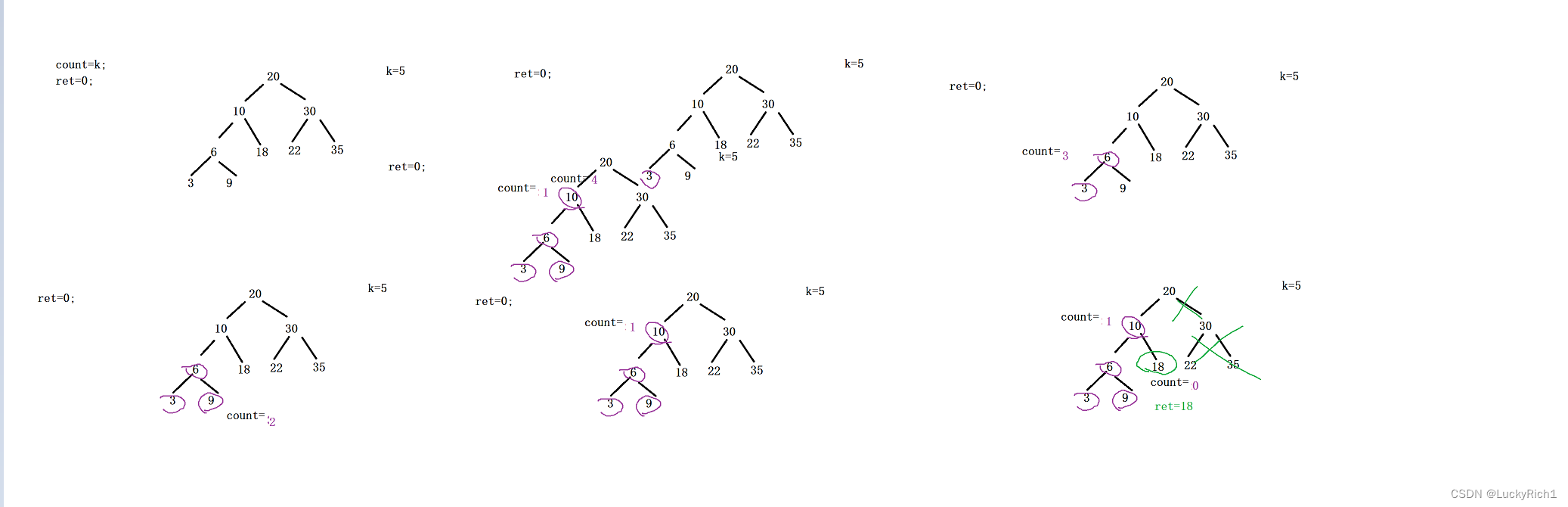
在这里插入图片描述

如果不使用全局遍历，就需要在递归函数中传参，并且还需要考虑参数在递归函数中如何改变。

class Solution {
    int count=0,ret=0;
public:
    int kthSmallest(TreeNode* root, int k) {

        count=k;
        dfs(root);
        return ret;
        // if(root == nullptr) return 0;

        // if(count <= k)
        //     kthSmallest(root->left,k);
        // ++count;
        // if(count == k)
        // {
        //     ret=root->val;
        // }
        // if (count <= k)
        //     kthSmallest(root->right,k);
        // return ret;

    }

    void dfs(TreeNode* root)
    {
        if(root == nullptr || count == 0) return;
        
        dfs(root->left);
        --count;
        if(count == 0) ret=root->val;
        dfs(root->right);
    }
};

6.二叉树的所有路径

题目链接：257. 二叉树的所有路径

题目分析：

在这里插入图片描述

题目很简单，让找根到叶子节点的所有路径。

算法原理：
这道题重点强调的还是

  1. 全局变量
  2. 回溯
  3. 剪枝

其中这道题最重要的是想说回溯 ----> “恢复现场” ，一定纠正思想 因为出现了回溯 才会想到要 恢复现场

只要出现递归必定会有回溯，既然回溯中有恢复现场，那就可以这样说，只要有深度优先遍历就有恢复现场的操作。只不过在简单题恢复现场这个动作并不明显，因为参数在递归过程中就已经自动恢复现场了，但是在一些难的题里面，一旦用到全局变量，我们要手动恢复，这个恢复现场操作就会变成额外重要。

比如这道题我们用两个全局变量，path是把根到叶子节点所经历的路径记录下来，ret是把path到叶子节点后的整条路径记录下来。
在这里插入图片描述

path遇到不是叶子节点就 值 + ->，遇到叶子就把path放到ret数组中。但是此时有一个超级致命的问题，回溯的时候，path要回到上一层，你会发现回溯到上一层path不应该有 4 的，因为path往其他子树传仅需要传 1->2-> 就行了！那此时就应该 恢复现场，把全局变量恢复下去之前的样子。此时还有一个问题如果把path设计成全局变量，回溯时path要不停pop，从叶子节点回溯还好说，但是从非叶子节点回溯要pop两次，挺麻烦的！

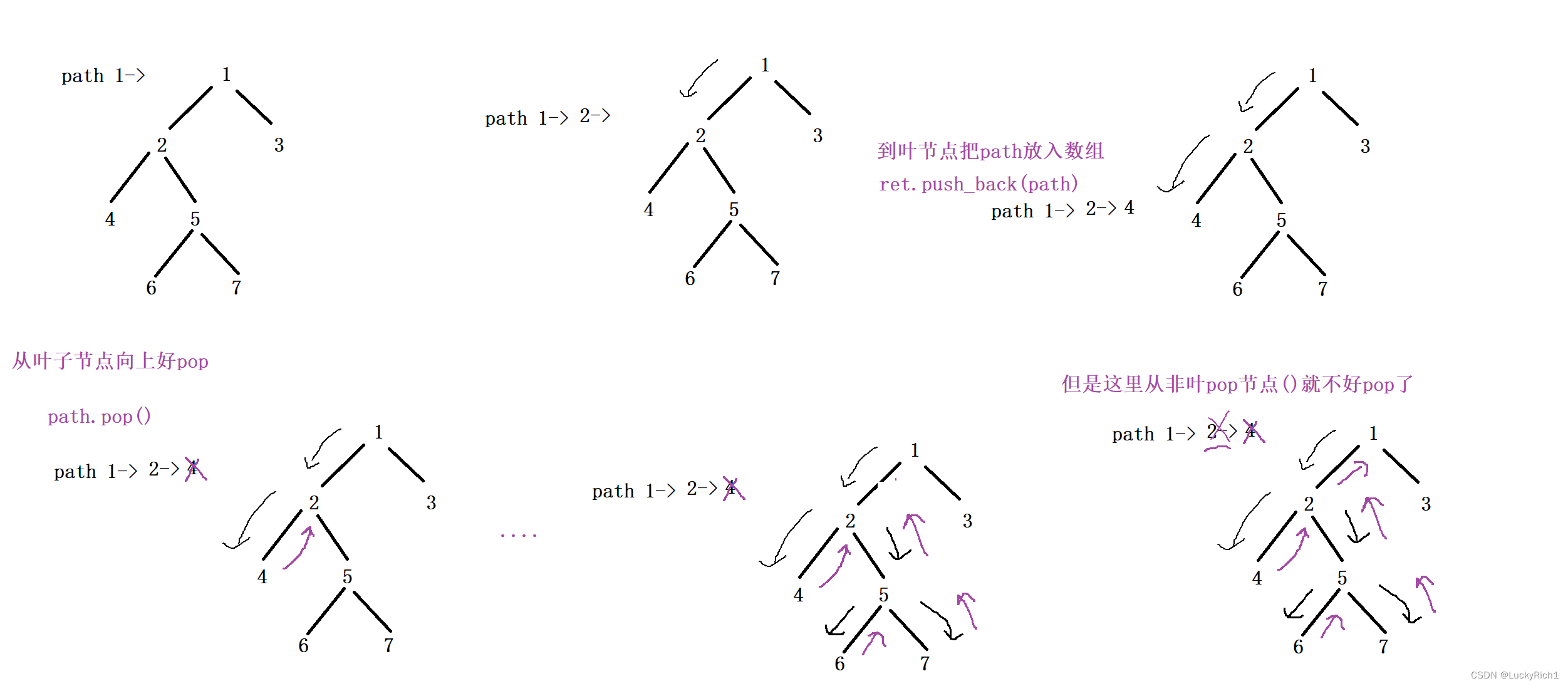
在这里插入图片描述

这道题用全局变量path记录路径比较麻烦，仅是这道题全局path不好用，但是比较麻烦的题全局path好用，这里只是为了说明，有恢复现场这个操作的。

这道题我们函数头这样设计 void dfs(root,path)，把path当成参数传给函数，你会发现恢复现场特别容易，函数特性就已经帮我们恢复现场了。因为每次函数都会重新创建一个path，回溯到上一层用的还是上一层自己的path。就不用自己手动恢复了。

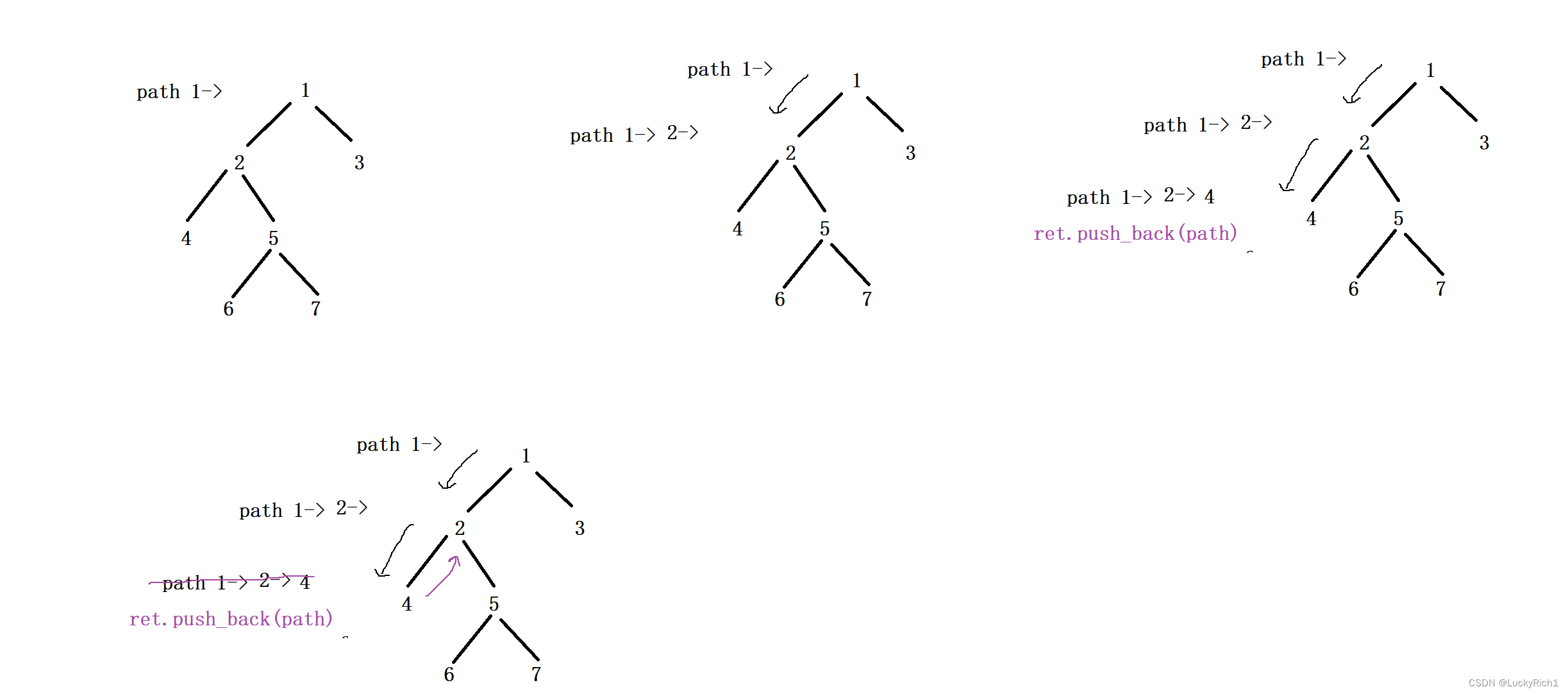
在这里插入图片描述

总结一下：全局变量 不好手动 恢复现场，那就 参数 自动 恢复现场

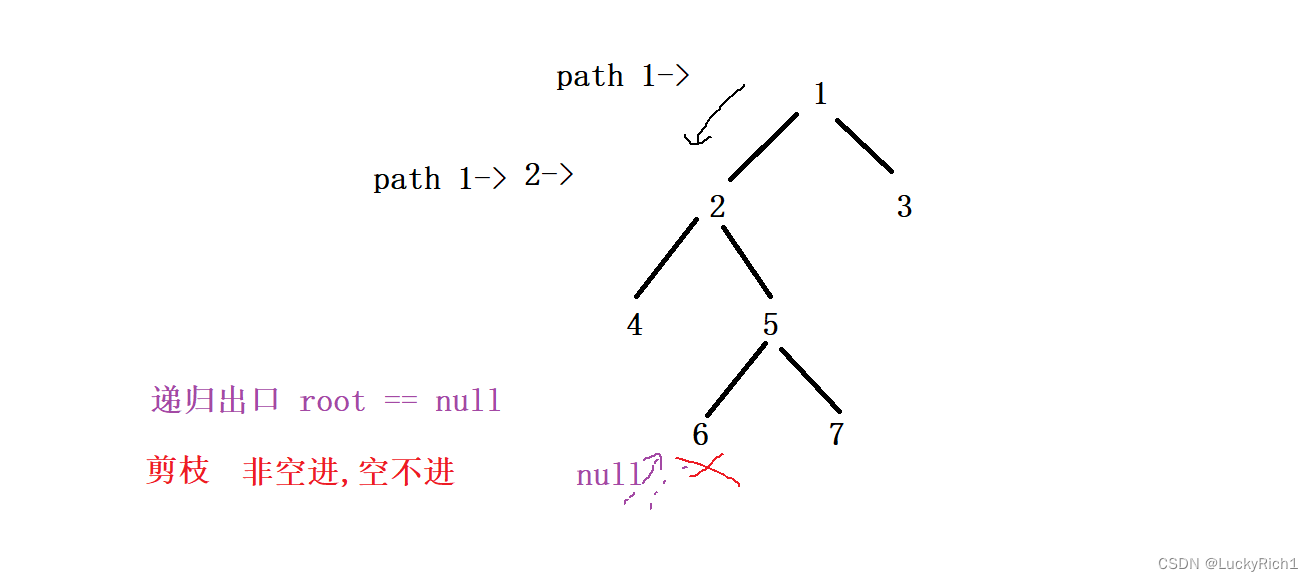
函数头，函数体都差不多了，接下来就是递归出口了，当root == nullptr 返回。但是这里递归还要进去才返回。此时我们可以剪枝，当非空进去，空就不要进！

在这里插入图片描述

class Solution {
    vector<string> ret;
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        string path;
        dfs(root,path);
        return ret;
    }

    void dfs(TreeNode* root,string path)
    {
        //if(root == nullptr) return;

        path+=to_string(root->val);
        if(root->left == nullptr && root->right == nullptr)
        {
            ret.push_back(path);
            return;
        }

        path+="->";
        // dfs(root->left,path);
        // dfs(root->right,path);

        //回溯+剪枝 if就是剪枝
        if(root->left) dfs(root->left,path);

        //中间如果有就是回溯

        if(root->right) dfs(root ->right,path);
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1797490.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【算法】深入浅出爬山算法：原理、实现与应用

【算法】深入浅出爬山算法：原理、实现与应用

人不走空 &#x1f308;个人主页&#xff1a;人不走空 &#x1f496;系列专栏&#xff1a;算法专题 ⏰诗词歌赋&#xff1a;斯是陋室&#xff0c;惟吾德馨 目录 &#x1f308;个人主页&#xff1a;人不走空 &#x1f496;系列专栏&#xff1a;算法专题 ⏰诗词歌…
阅读更多...
python-小游戏-弹球对决

python-小游戏-弹球对决

python-小游戏-弹球对决 需要安装pygame 代码—game-Pong.py import pygame import random# Initialize pygame pygame.init()# Set up the screen WIDTH 600 HEIGHT 400 BALL_RADIUS 20 PAD_WIDTH 10 PAD_HEIGHT 80 WHITE (255, 255, 255) PURPLE (128, 0, 128) RED…
阅读更多...
Springboot注意点

Springboot注意点

1.Usermapper里加param注解 2.RequestParam 和 RequestBody的区别&#xff1a; RequestParam 和 RequestBody的区别&#xff1a; RequestParam 和 RequestBody 是Spring框架中用于处理HTTP请求的两个不同的注 get请求一般用url传参数&#xff0c;所以参数名和参数的值就在ur…
阅读更多...
Office(Microsoft 365) 体验

Office(Microsoft 365) 体验

Office 现已更名为 Microsoft 365。 Microsoft 365 是订阅服务&#xff0c;订阅期间可享受定期的功能与安全更新&#xff0c;始终使用的是的最新版本。 Microsoft 365 包含 Word、Excel、PowerPoint 等办公常用套件&#xff0c;还包括了 OneDrive、Exchange 等协作和通信工具…
阅读更多...
视觉SLAM十四讲：从理论到实践（Chapter11：回环检测）

视觉SLAM十四讲：从理论到实践（Chapter11：回环检测）

前言 学习笔记&#xff0c;仅供学习&#xff0c;不做商用&#xff0c;如有侵权&#xff0c;联系我删除即可 一、主要目标 1.理解回环检测的必要性。 2.掌握基于词袋的外观式回环检测。 3.通过DBoW3的实验&#xff0c;学习词袋模型的实际用途。 二、概述 VO存在误差累积&…
阅读更多...
SpringBoot发送邮件带附件的服务如何实现？

SpringBoot发送邮件带附件的服务如何实现？

SpringBoot发送邮件带附件的步骤&#xff1f;怎么配置邮件服务&#xff1f; SpringBoot作为一款轻量级的Java框架&#xff0c;以其便捷的配置和强大的功能受到开发者的广泛欢迎。AokSend将详细介绍如何在SpringBoot中实现发送带附件的邮件服务。 SpringBoot发送邮件带附件&am…
阅读更多...
【全开源】Workerman在线客服系统（ThinkPHP+FastAdmin+Workerman）

【全开源】Workerman在线客服系统（ThinkPHP+FastAdmin+Workerman）

Workerman在线客服系统&#xff1a;高效沟通的新选择 基于ThinkPHPFastAdminWorkerman开发的一款实时在线客服系统&#xff0c;支持多客服(不限座席)、知识库、离线留言板、离线消息、历史会话、微信小程序接入、Uni-app接入(高级授权)、用户轨迹等功能。​ &#x1f4e2; 一…
阅读更多...
2024年全国青少信息素养大赛图形化编程挑战赛集训第一天编程题分享

2024年全国青少信息素养大赛图形化编程挑战赛集训第一天编程题分享

大家如果不想阅读前边的比赛内容介绍，可以直接跳过：拉到底部看集训第一天题目 （一）比赛内容: 【小学低年级组】 1、图形化编程软件的使用：熟悉图形化编程软件中舞台区、角色列表区、功能区、脚本编 -3- 辑区的功能及使用。 2、基础功能模块的使用： a.运动模块：角…
阅读更多...
day52 123.买卖股票的最佳时机III 188.买卖股票的最佳时机IV

day52 123.买卖股票的最佳时机III 188.买卖股票的最佳时机IV

123.买卖股票的最佳时机III 关键在于至多买卖两次&#xff0c;这意味着可以买卖一次&#xff0c;可以买卖两次&#xff0c;也可以不买卖。 动态规划五部曲 1.确定dp数组以及下标的含义 一天一共就有五个状态&#xff0c; 没有操作 &#xff08;其实我们也可以不设置这个状态&a…
阅读更多...
Qt 窗口居中显示

Qt 窗口居中显示

Qt 窗口居中显示 引言一、窗体的setGeometry函数二、计算屏幕中心然后move三、借助QRect计算四、补充知识点 引言 窗口居中可以提供良好的视觉效果、突出重点内容、提升用户导航和操作的便利性&#xff0c;有助于改善用户体验。 Qt一般情况下&#xff0c;其Mainwindow或弹出的…
阅读更多...
学习笔记——IP地址网络协议——CIDR无类别域间路由

学习笔记——IP地址网络协议——CIDR无类别域间路由

五、CIDR无类别域间路由 1、CIDR的介绍 无类域间路由(Classless Inter Domain Routing&#xff0c;CIDR)也称为&#xff1a;超网(supernetting)由RFC1817定义。CIDR突破了传统IP地址的分类边界&#xff0c;将路由表中的若干条路由汇聚为一条路由&#xff0c;减少了路由表的规…
阅读更多...
河南市政环境卫生乙级资质：人员准备要点

河南市政环境卫生乙级资质：人员准备要点

河南市政环境卫生乙级资质申请在人员准备方面&#xff0c;需要满足一系列的要求和标准。以下是人员准备的要点&#xff0c;按照清晰、分点的方式进行归纳&#xff1a; 一、注册类工程师 注册二级建筑师&#xff1a;至少1名&#xff0c;负责市政环境卫生工程中的建筑设计及相关…
阅读更多...
Vue3【七】setup的语法糖setup简写方法

Vue3【七】setup的语法糖setup简写方法

Vue3【七】setup的语法糖setup简写方法 Vue3【七】setup的语法糖setup简写方法 使用script标签式写法称为setup语法糖 组件名称默认位文件名 export 的内容可以省略 案例截图 案例目录 案例代码 Person.vue <template><div class"person"><h1>我…
阅读更多...
美颜SDK与直播美颜插件：开发者指南与优化技巧

美颜SDK与直播美颜插件：开发者指南与优化技巧

本篇文章&#xff0c;小编将详细探讨如何利用美颜SDK和直播美颜插件进行开发&#xff0c;以及在实际应用中优化这些工具的技巧。 一、美颜SDK简介 美颜SDK这些功能通过复杂的图像处理算法实现&#xff0c;SDK的存在大大简化了开发者的工作&#xff0c;使他们无需从零开始编写…
阅读更多...
酷我音乐 v10.8.2.1 解索SVIP版，畅享无界音乐盛宴！

酷我音乐 v10.8.2.1 解索SVIP版，畅享无界音乐盛宴！

酷我音乐 v10.8.2.1 解索SVIP版 酷我音乐&#xff0c;一款多功能音乐软件&#xff0c;集成了音乐播放、歌曲下载、歌词同步、在线电台等多项服务。该应用致力于提供高品质的音乐欣赏体验和独特的音乐探索机会&#xff0c;无论用户身处何地。此外&#xff0c;它还支持大量付费高…
阅读更多...
STM32项目分享：智能家居安防系统

STM32项目分享：智能家居安防系统

目录 一、前言 二、项目简介 1.功能详解 2.主要器件 三、原理图设计 四、PCB硬件设计 1.PCB图 2.PCB板及元器件图 五、程序设计 六、实验效果 七、资料内容 项目分享 一、前言 项目成品图片&#xff1a; 哔哩哔哩视频链接&#xff1a; https://www.bilibili.c…
阅读更多...
倩女幽魂游戏攻略：24小时辅助云手机选哪家好？

倩女幽魂游戏攻略：24小时辅助云手机选哪家好？

在《倩女幽魂》中&#xff0c;玩家经常需要长时间挂机以完成任务和提升等级。选择合适的云手机软件可以大大提升游戏效率。以下是选择VMOS云手机作为挂机软件的几个理由&#xff1a; 多开应用支持 VMOS云手机允许用户在虚拟环境中同时运行多个应用程序&#xff0c;这包括多个…
阅读更多...
MyBatis总结（2）- MyBatis实现原理（一）

MyBatis总结（2）- MyBatis实现原理（一）

Mybatis实现原理&#xff1a; 概括一句话&#xff1a;约定配置参数mybatis-config.xml&#xff0c;映射关系JavaBean-mapper.xml&#xff0c;用SqlSessionFactoryBuilder构建应用程序运行期间需要的SqlSessionFactory实例对象&#xff0c;当请求或方法需要执行CURD操作时&…
阅读更多...
3DGS语义分割之LangSplat

3DGS语义分割之LangSplat

LangSplat是CVPR2024的paper. 实现3DGS的语义分割&#xff08;可文本检索语义&#xff09; github: https://github.com/minghanqin/LangSplat?tabreadme-ov-file 主要思想是在3DGS中加入了CLIP的降维语义特征&#xff0c;可用文本检索目标&#xff0c;实现分割。 配置环境&…
阅读更多...
[office] Excel数据透视表有什么用途？Excel数据透视表怎么做？ #学习方法#职场发展

[office] Excel数据透视表有什么用途？Excel数据透视表怎么做？ #学习方法#职场发展

Excel数据透视表有什么用途&#xff1f;Excel数据透视表怎么做&#xff1f; Excel数据透视表是一种数据汇总手段&#xff0c;如果表格内的数据太多&#xff0c;单靠肉眼是很难准确分辨数据的&#xff0c;而使用数据透视表&#xff0c;就可以很方便的筛选各种数据。如果你不知道…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023