【因果推断python】21

【因果推断python】21_匹配2

news2024/10/6 4:31:14

匹配估计器

子分类估计器在实践中用得不多（我们很快就会明白为什么，主要是因为维度诅咒这个原因），但它让我们很好地、直观地了解了因果推理估计器应该做什么，以及它应该如何控制混淆因素。这使我们能够探索其他类型的估计器，例如匹配估计器。

这个想法非常相似。由于某种混淆因素 X 使得经过干预的和未干预的样本单元最初无法比较，我可以通过将每个经过干预的单元与类似的未经干预的单元匹配来做到这一点。这就像我为每个干预单元找到一个未经干预的双胞胎。通过进行这样的比较，干预过的和未经干预的样本再次变得可比较。

举个例子，假设我们试图估计一个练习生训练计划对收入的影响。这是练习生的基本情况：

trainee = pd.read_csv("./data/trainees.csv")
trainee.query("trainees==1")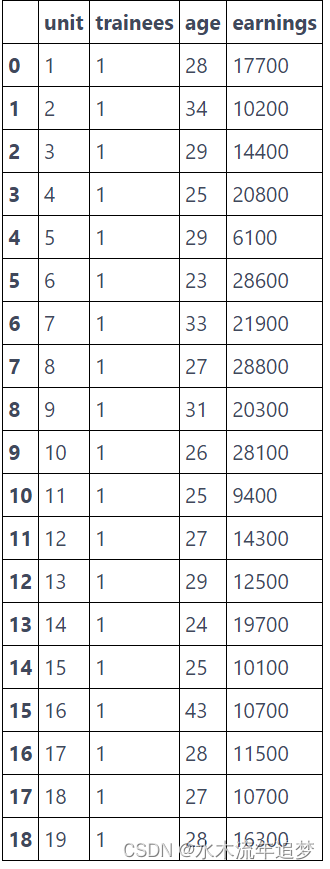

下面是非练习生的基本情况：

如果我对均值做一个简单比较，我们会发现那些练习生相比非练习生赚的更少。

但是，如果我们看一下上面的表格，我们会注意到练习生比非练习生年轻得多，这表明年龄可能是一个混淆因素。让我们使用年龄匹配来尝试纠正这一点。我们将从接受干预的人那里取出1号单元，并将其与27号单元配对，因为两者都是28岁。对于单元2，我们将它与单元34配对，而单元3则与单元37配对，对于单元4我们将它与单元35配对...当涉及到5号单元时，我们需要从未接受干预的人中找到29岁的人，但那是37号单元，它已经配对了。这其实不是问题，因为我们可以多次使用相同的单元。如果可以匹配的单位超过1个，我们可以在它们之间随机选择。

这是前 7 个单元在匹配后的数据集中的样子：

# make dataset where no one has the same age
unique_on_age = (trainee
                 .query("trainees==0")
                 .drop_duplicates("age"))

matches = (trainee
           .query("trainees==1")
           .merge(unique_on_age, on="age", how="left", suffixes=("_t_1", "_t_0"))
           .assign(t1_minuts_t0 = lambda d: d["earnings_t_1"] - d["earnings_t_0"]))

matches.head(7)

请注意，最后一列的收益差额为已干预单元和与其匹配的未干预单位之间的差异。如果我们取最后一列的平均值，我们得到控制年龄情况下的ATET估计值。请注意，与之前我们使用简单均值差值的估计值相比，该估计值现在显著为正。

matches["t1_minuts_t0"].mean()

2457.8947368421054

但这是一个人为设置的例子，只是为了引入匹配这个概念。实际上，我们通常有多个特征，并且单元间也是不能完全可以匹配。在这种情况下，我们必须定义一些接近度的测量值，以比较单元之间的接近程度。一个常见的指标是欧几里得范数 $||X_i-X_j||$ 。但是，这种差异在特征的大小变化时并不是保持不变。这意味着，与收入等量纲更大的特征相比，在计算此范数时，类似年纪这种以十分之一为单位的特征的重要性要小得多。因此，在应用范数之前，我们需要缩放特征的值，使它们具有大致相同的比例。

定义了距离的测度指标后，我们现在可以将匹配定义为寻找要匹配的样本的最近邻居。在数学方面，我们可以通过以下方式编写匹配估计器：

$\hat{ATE}=\frac1N\sum_{i=0}^N(2T_i-1)\big(Y_i-Y_{jm}(i)\big)$

其中 $Y_{jm}(i)$ 是来自与 $Y_{i}$ 最相似的另一个干预组的样本。我们这样做 $2T_{i}-1$ 次，并以两种方式匹配：从干预组匹配对照组样本，以及从对照组匹配干预样本。

为了测试这个估计器，让我们考虑一个医学示例。跟上次一样，我们想找到药物对病人恢复时间长短的效果。不幸的是，这种影响被疾病的严重程度、性别以及年龄所混淆。我们有理由相信，病情更严重的患者接受药物治疗的机会更高。

med = pd.read_csv("./data/medicine_impact_recovery.csv")
med.head()

如果我们看一个简单的均值差， $E[Y|T=1]-E[Y|T=0]$ ，我们得到受到治疗的病人平均需要比未接受治疗的病人多16.9天才能恢复。这可能是由于混淆，因为我们不认为药物会对患者造成伤害。

med.query("medication==1")["recovery"].mean() - med.query("medication==0")["recovery"].mean()

16.895799546498726

为了纠正这个偏差，我们需要使用匹配来控制X。首先，我们一定要记得缩放我们的特征，否则，类似年龄这样的特征在我们计算两个样本点间距离的时候，会比严重性这种特征有更高的重要性。我们可以通过对特征进行归一化的方式来解决这个问题。

# scale features
X = ["severity", "age", "sex"]
y = "recovery"

med = med.assign(**{f: (med[f] - med[f].mean())/med[f].std() for f in X})
med.head()

现在，到匹配本身。我们将使用来自 Sklearn 的 K 最近邻算法，而不是编写匹配函数。此算法通过在估计或训练集中查找最近的数据点来进行预测。

为了匹配，我们需要其中的2个函数。一个是; mt0 ，它将存储未干预的样本，并在被要求时在未处理的点中找到匹配项。另一个，mt1，将存储被干预的样本，并在需要时在被干预的样本点中找到匹配项。在此拟合步骤之后，我们可以使用这些 KNN 模型进行预测，从而是我们的匹配样本。

from sklearn.neighbors import KNeighborsRegressor

treated = med.query("medication==1")
untreated = med.query("medication==0")

mt0 = KNeighborsRegressor(n_neighbors=1).fit(untreated[X], untreated[y])
mt1 = KNeighborsRegressor(n_neighbors=1).fit(treated[X], treated[y])

predicted = pd.concat([
    # find matches for the treated looking at the untreated knn model
    treated.assign(match=mt0.predict(treated[X])),
    
    # find matches for the untreated looking at the treated knn model
    untreated.assign(match=mt1.predict(untreated[X]))
])

predicted.head()