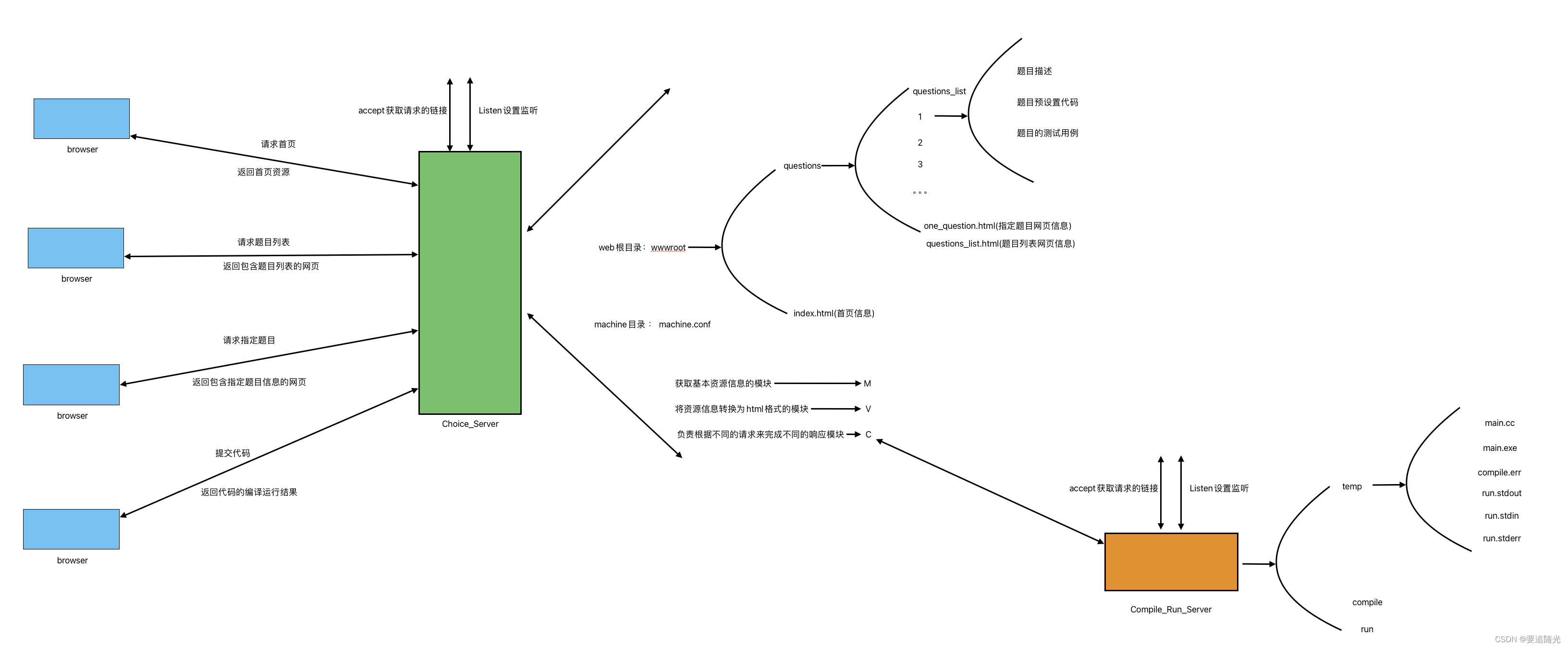
根据往年考试题,对考点和知识点的一个整理。
校验编码
码距
一种编码的最小码距,其实就是指这种编码的码距。码距有两种定义:
| 码距所描述的对象 | 含义 |
|---|---|
| 2 2 2 个特定的码 | 其二进制表示中不同位的个数 |
| 一种编码 | 这种编码中任意 2 2 2 个合法编码的最小码距 |
课本上出现的码及其码距归纳如下。
- 奇偶校验码的码距是 2 2 2。
- 能纠 1 1 1 位错的海明码的码距始终是 3 3 3,不管 n , k , r n,k,r n,k,r 如何变化。首先,海明码的每一个数据位至少位于 2 2 2 个校验组,这就保证了海明码的码距至少是 3 3 3;其次, H 3 H_3 H3 一定位于且仅位于 G 1 , G 2 G_1,G_2 G1,G2 校验组, H 3 H_3 H3 的变化引起且只引起 P 1 , P 2 P_1,P_2 P1,P2 的变化,从而构造了一对码距为 3 3 3 的合法编码,保证海明码的码距最多是 3 3 3。
- CRC 编码的码距不固定,但是至少是 3 3 3。不同的 ( n , k ) (n,k) (n,k) 和生成多项式对应了不同的码距。比如下面这张表(来源于这篇博客):
| 总位数 n n n | 数据位数 k k k | 生成多项式 G ( x ) G(x) G(x) | G ( x ) G(x) G(x) 的二进制表示 | 码距 |
|---|---|---|---|---|
| 7 7 7 | 4 4 4 | x 3 + x + 1 x^3+x+1 x3+x+1 | 1011 1011 1011 | 3 3 3 |
| 7 7 7 | 4 4 4 | x 3 + x 2 + 1 x^3+x^2+1 x3+x2+1 | 1101 1101 1101 | 3 3 3 |
| 7 7 7 | 3 3 3 | x 4 + x 3 + x 2 + 1 x^4+x^3+x^2+1 x4+x3+x2+1 | 11101 11101 11101 | 4 4 4 |
| 7 7 7 | 3 3 3 | x 4 + x 2 + x + 1 x^4+x^2+x+1 x4+x2+x+1 | 10111 10111 10111 | 4 4 4 |
| 15 15 15 | 11 11 11 | x 4 + x + 1 x^4+x+1 x4+x+1 | 10011 10011 10011 | 3 3 3 |
| 15 15 15 | 7 7 7 | x 8 + x 7 + x 6 + x 4 + 1 x^8+x^7+x^6+x^4+1 x8+x7+x6+x4+1 | 111010001 111010001 111010001 | 5 5 5 |
| 31 31 31 | 26 26 26 | x 5 + x 2 + 1 x^{5}+x^{2}+1 x5+x2+1 | 100101 100101 100101 | 3 3 3 |
| 31 31 31 | 21 21 21 | x 10 + x 9 + x 8 + x 6 + x 5 + x 3 + 1 x^{10}+x^{9}+x^{8}+x^{6}+x^{5}+x^{3}+1 x10+x9+x8+x6+x5+x3+1 | 11101101001 11101101001 11101101001 | 5 5 5 |
| 63 63 63 | 57 57 57 | x 6 + x + 1 x^{6}+x+1 x6+x+1 | 1000011 1000011 1000011 | 3 3 3 |
| 63 63 63 | 51 51 51 | x 12 + x 10 + x 5 + x 4 + x 2 + 1 x^{12}+x^{10}+x^{5}+x^{4}+x^{2}+1 x12+x10+x5+x4+x2+1 | 1010000110101 1010000110101 1010000110101 | 5 5 5 |
汉字编码实验
GB2312 码:占
2
2
2 个字节,每个字节的最高位都是
1
1
1(为了与 ASCII 码区分)。
区号:GB2312 码高字节的低
7
7
7 位。
位号:GB2312 码低字节的低
7
7
7 位。
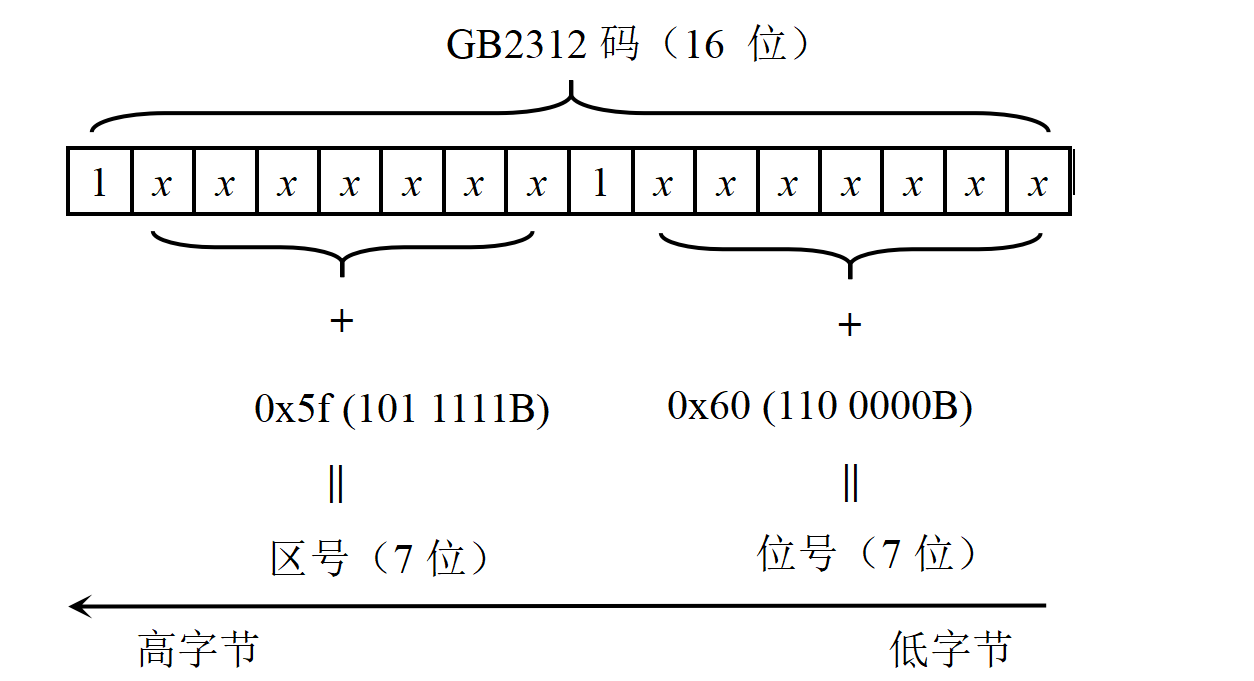
国标码转区位码的流程如下:
海明码流水传输实验
有关海明码的其它实验以及海明码的概念,可以参看这篇博客。这篇博客没有涉及到海明码的流水传输,在这里回顾一下。CRC 编码的流水传输和海明码流水传输在构成上是相似的。
流水传输的过程如下所示。图中的~使能/Stall 信号通过各级锁存器依次向右传递,获取了使能的锁存器将在下一个时钟上升沿完成锁存。当发生两位错的时候,前三个锁存器的值清零,同时地址回滚(减
3
3
3),显示阶段的锁存器stall接收到的数据
3
3
3 个时钟周期。

这是电路复位后的状态:
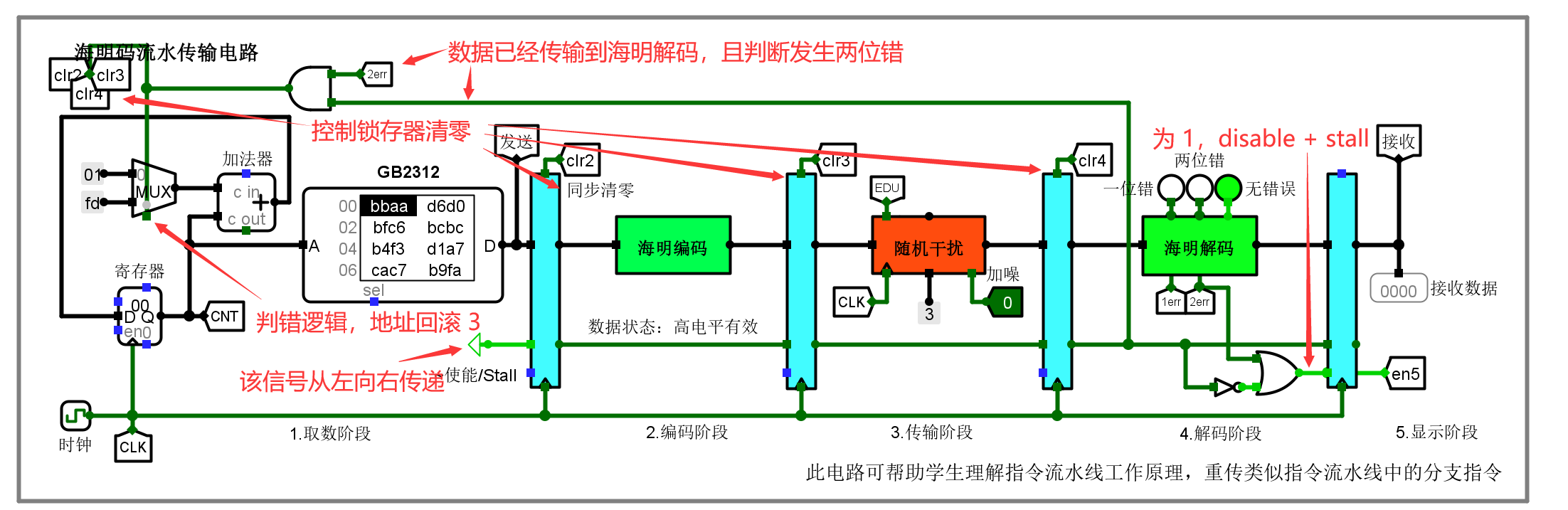
据此,总结两位错时各阶段的动作得下表:
| 阶段 | 动作 | 备注 |
|---|---|---|
| 取数阶段 | 地址回滚 | 地址要回滚 3 3 3 个汉字(ROM 回滚 6 6 6 个字节),出错了的数据重新传输。 |
| 编码阶段 | 数据清零 | 这个清零其实核心是把数据状态的值置为 0 0 0,其中锁存的数据可以不用管。 |
| 传输阶段 | 数据清零 | 和编码阶段清零是一个道理。 |
| 显示阶段 | 数据锁存 | 出错的字重传需要 3 3 3 个时钟周期才能到达显示阶段的锁存器,在这段时间内需要维持上一个字的显示。 |
CRC 编码解码
课本上介绍了 CRC编码、解码的时序逻辑实现,原始数据 D k ⋯ D 1 D_k\cdots D_1 Dk⋯D1 按位串行输入进来,然后经过时序系统的处理,每个时钟周期产出一位余数。但是我们做实验时用组合逻辑实现,根据 16 16 16 位原始数据 D 1 D_1 D1~ D 16 D_{16} D16 直接得到 6 6 6 校验码 R 1 R_1 R1~ R 6 R_6 R6。
实验中有两种思路,一种是采用 6 6 6 位的生成多项式,得到 5 5 5 位余数且 R 6 R_6 R6 作为总偶校验位;另一种是采用 7 7 7 位的生成多项式,得到 6 6 6 位的余数,就不设总偶校验位了。我当时没有想到后一种,因为它放了个 P P P 作为总偶校验位,还以为 R 6 R_6 R6 就是 P P P(心虚)。
头歌上萝卜打表没打全,能用的 6 6 6 位生成多项式只有下面这个:

上面的表是课本上的。使用这个生成多项式,直接出现了余数相等的盛况:
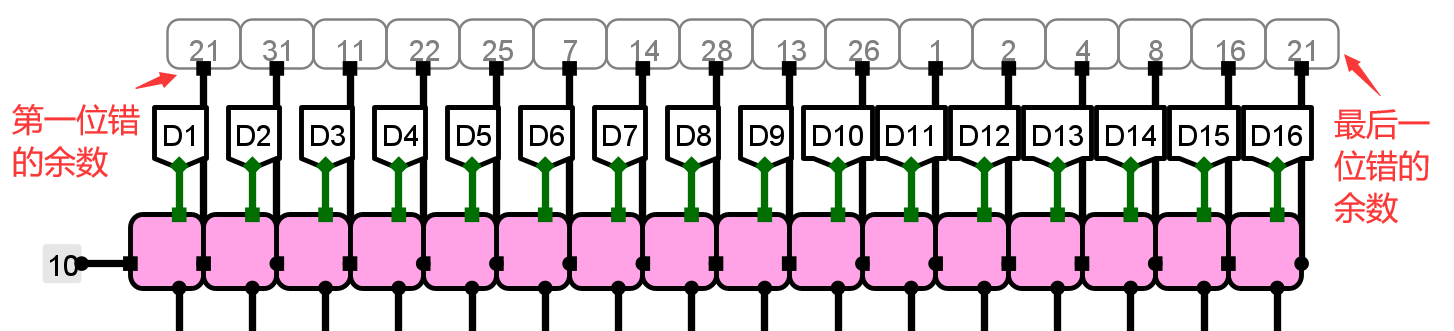
那么这个生成多项式显然在这里
(
k
=
16
)
(k=16)
(k=16) 是不能用的,只有原始数据是
15
15
15 位及以下才能用。其实表格上面的
x
5
+
x
3
+
1
(
0
x
29
)
x^5+x^3+1(0\rm x29)
x5+x3+1(0x29) 和
x
5
+
x
2
+
1
(
0
x
25
)
x^5+x^2+1(0\rm x 25)
x5+x2+1(0x25) 都可以使用,但是当时做实验的时候没有关注到课本,自己捏了一个
x
5
+
x
3
+
x
2
+
x
+
1
(
0
x
2
f
)
x^5+x^3+x^2+x+1(0\rm x2f)
x5+x3+x2+x+1(0x2f) 来用。
上面出现的这三个
(
0
x
29
,
0
x
25
,
0
x
2
f
)
(\rm{0x29,0x25,0x2f})
(0x29,0x25,0x2f) 都是可以纠正一位错的。考题里现在出现了这样一个问题:
在假定没有 3 3 3 位以上错误发生的前提下,你的生成多项式生成的 CRC 编码检错时能否区分 1 1 1 位错和 2 2 2 位错?

对于我的版本(多项式 6 6 6 位),答案说是不能区分,余数相同。果真余数相同吗?我们利用下面的代码,尝试一下上面三个生成多项式。
#include<iostream>
int poly,rest[23] = {0x1};
bool bkt[100],bkt2[900],retag;
inline int bitcount(int num){
int ret = 0;
while(num){
ret++;
num >>= 1;
}
return ret;
}
inline int getRest(int num){return bitcount(num) == bitcount(poly)?(num ^ poly):num;}
int main(){
int restnum;
scanf("%x",&poly);
for(int i = 1;i < 22;i++){
rest[i] = getRest(rest[i-1] << 1);
if(rest[i] == 0)
return printf("一位错:第 %d 位错的余数是 0."),0;
if(bkt[rest[i]])
return printf("一位错:余数重复."),0;
bkt[rest[i]] = true;
}
for(int i = 0;i < 22;i++)
for(int j = i + 1;j < 22;j++){
restnum = getRest(rest[i] ^ rest[j]);
if(restnum == 0)
return printf("两位错(%d,%d)的余数是 0.",i,j),0;
if(bkt[restnum])
return printf("两位错(%d,%d)与一位错余数(%d)重复.",i,j,restnum),0;
if(bkt2[restnum])
retag = true;
bkt2[restnum] = true;
}
printf(retag?"存在两位错余数重复.":"无重复.");
return 0;
}
结果是:
in: 0x2f out: 两位错(0,1)与一位错余数(3)重复.
in: 0x29 out: 两位错(0,1)与一位错余数(3)重复.
in: 0x25 out: 两位错(0,1)与一位错余数(3)重复.
那么这三个生成多项式,确实二位错和一位错的余数会重复,答案说得对。至于 7 7 7 位生成多项式的情况,一位错和二位错的余数是不是真的不相同,尝试了同学提供的生成多项式 0 x 6 f \rm 0x6f 0x6f:
in: 0x6f out: 存在两位错余数重复.
可见就这个生成多项式而言,确实是能够区分两位错和一位错的,因此试卷上的答案没有问题。
Cache 与虚拟存储系统
k
−
k-
k−路组相连,指的是每一个 cache 组有
k
k
k 个 cache 行(或者说
k
k
k 个数据块)。这里主要说一下 TLB 这个特殊的 cache 是怎么组织的。
TLB 作为一个 cache,自然也有全相联、直接相联和组相联三种方式。以
k
−
k-
k−路组相联为例对比一下 TLB 和内存 cache。
| Cache 类型 | 映射方式 | t a g \mathit{tag} tag 字段来源 | i n d e x \mathit{index} index 字段位数 | 有无块内偏移 ( o f f s e t ) (\mathit{offset}) (offset)字段 |
|---|---|---|---|---|
| TLB | 标记 t a g \mathit{tag} tag → P P N \mathit{PPN} PPN | V P N \mathit{VPN} VPN | log 2 k \log_2k log2k | 无 |
| 内存 cache | 标记 t a g \mathit{tag} tag → 内存数据块 | 内存地址 | log 2 k \log_2k log2k | 有 |
它们最大的区别就是,TLB 中是没有 o f f s e t \mathit{offset} offset 字段的。内存 cache 是通过 t a g \mathit{tag} tag 字段找到对应的数据块,然后根据 o f f s e t \mathit{offset} offset 字段寻找对应的字节(或者字,看计算机按什么编址了);TLB 直接通过 t a g \mathit{tag} tag 字段找到对应的 P P N \mathit{PPN} PPN,不需要 o f f s e t \mathit{offset} offset 字段。这也就意味着 TLB 行的开销比内存 cache 行小很多。

指令系统
课本是以 MIPS 指令集讲解的这一章,而 MIPS 指令集中,R 型指令的操作码字段 o p \mathit{op} op 一定是为 0 0 0 的,R 型指令中不同功能的指令根据 f u n c t \mathit{funct} funct 字段来区分。

其中beq属于上面的 I 型指令,立即数字段时跳转的偏移量。这里的偏移量指的是从下一条指令开始,偏移多少条指令,而不是多少字节或者多少字。对于 MIPS32 而言,其指令字长是恒定的
32
32
32 位,即
4
B
4\rm B
4B,那么beq中立即数为
i
i
i 意味着要偏移
4
i
4i
4i 个字节。
CPU 设计
数据通路时间相关问题
如下图,总结了就是两个条件,对于时钟周期,要求有 T c l o c k > T c l k _ t o _ Q + T m a x + T s e t u p T_{\mathit{clock}}>T_{\mathit{clk\_to\_Q}}+T_\mathit{max}+T_\mathit{setup} Tclock>Tclk_to_Q+Tmax+Tsetup。对于寄存器的 hold time 也有要求: T h o l d < T c l k _ t o _ Q + T m i n T_\mathit{hold}<T_{\mathit{clk\_to\_Q}}+T_\mathit{min} Thold<Tclk_to_Q+Tmin。


状态机
这里说的都是无中断的状态机。
传统的三级时序和现代时序是不一样的。三级时序中,每个机器周期都包含 4 4 4 个时钟周期,而现代时序的计算、执行分别为 2 , 3 2,3 2,3 个时钟周期。它们的电路也是不一样:

三级时序中,时序发生器有一个状态机。硬布线控制器作为一个组合逻辑单元,其输出不给到时序发生器,所以应该将它和时序发生器割裂开来。这个时序发生器的状态机如下图左:


现代时序中,其实也可以弄一个时序发生器,相比于三级时序的时序发生器,少了 2 2 2 个计算周期和 1 1 1 个执行周期。如上图右所示。但是如果要用 FSM 状态机的话,响应的状态转换图如下:

这个是将 FSM 状态机和状态寄存器看作一个整的时序逻辑电路,构造出来的状态图;不是 FSM 单独的状态图,组合逻辑电路没有所谓状态图。同时注意一下所有状态中访问内存的那些状态,以及给出的READ/WRITE信号。
中断的实现方式
主要是开中断和关中断实现方式的区别:
| 中断操作 | 实现方式 | 具体 |
|---|---|---|
| 关中断 | 硬件实现 | 中断响应周期,由硬件完成 |
| 开中断 | 软件实现 | 中断返回时,eret指令将
I
E
\mathit{IE}
IE 置为
1
1
1 |
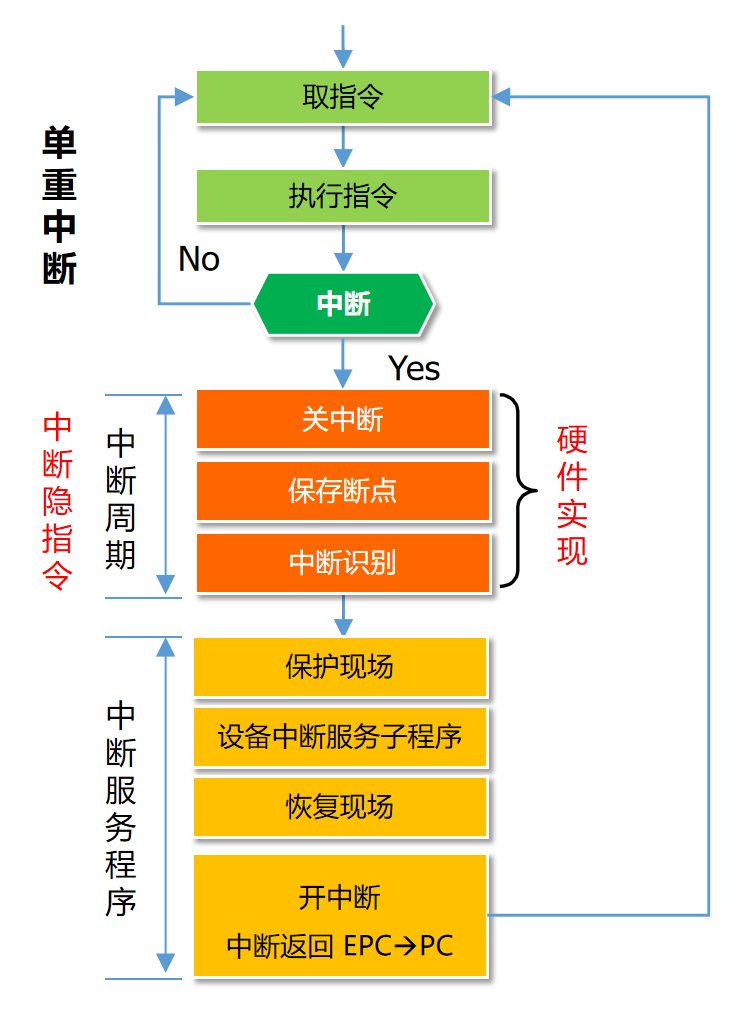
具体可以参考下面这两张图。其中中断响应是由硬件完成的操作,中断响应不是中断服务。中断响应周期结束后, P C \mathit{PC} PC 已然是中断服务程序的地址了,中断服务程序通过取指-计算-执行按指令一条条完成。

输入输出系统
DMA 与程序中断的区别:
1
1
1.中断通过程序传送数据,DMA靠硬件来实现。
2
2
2.中断时机为两指令之间,DMA响应时机为两存储周期之间。
3
3
3.中断不仅具有数据传送能力,还能处理异常事件。DMA只能进行数据传送。
4
4
4.DMA仅挪用了一个存储周期,不改变CPU现场。
5
5
5.DMA请求的优先权比中断请求高。CPU优先响应DMA请求,是为了避免DMA所连接的高速外设丢失数据。
6
6
6.DMA利用了中断技术