【关于傅里叶变换的一系列问题】

1. 为什么频率分辨率是 $\frac{f_s}{N}$ ？

因为采样率 ${f_s}$ 决定了最大频率范围（奈奎斯特频率）。
时域信号长度 𝑁决定了频域中的离散点数。DFT对长度为 𝑁的时域信号进行变换，得到频域信号
𝑋(𝑘)，其中 𝑘 是频率索引，范围为 0,1,2,…,𝑁−1
因此，每个频率分量之间的间隔由采样率和点数的比值决定。即，DFT要求在采样率范围内，存在均匀分布的N个频点，所以分辨率为 $\frac{f_s}{N}$ 。

2. 傅里叶变换为什么使用正弦和余弦函数来与信号相乘，仅仅用一个正弦或余弦函数可以吗？

要理解为什么单独使用正弦函数不能捕捉到信号的偶数对称部分，我们需要深入探讨信号的奇偶对称性和傅里叶变换的基础。

信号的奇偶对称性

一个信号 $x (t)$ 可以分解成奇函数部分 $x_{\text{odd}}(t)$ 和偶函数部分 $x_{\text{even}}(t)$ ：

$x_{\text{even}}(t) + x_{\text{odd}}(t)$

其中：

偶函数满足 $x_{\text{even}}(t) = x_{\text{even}}(-t)$
奇函数满足 $x_{\text{odd}}(t) = -x_{\text{odd}}(-t)$

正弦和余弦函数的正交性

正弦和余弦函数是相互正交的，即在一个周期内，它们的内积为零。正交性使得傅里叶变换能够将信号分解成互不干扰的独立频率成分。

正弦函数 $\sin(\omega t)$ 是奇函数，因为 $\sin(-\omega t) = -\sin(\omega t)$ 。
余弦函数 $\cos(\omega t)$ 是偶函数，因为 $\cos(-\omega t) = \cos(\omega t)$ 。

正弦函数和偶数对称部分

由于正弦函数是奇函数，它只能有效地表示信号的奇数对称部分。在傅里叶变换中，任何信号可以用正弦和余弦函数的组合来表示：

$\sum_{k=-\infty}^{\infty} \left( a_k \cos(\omega_k t) + b_k \sin(\omega_k t) \right)$

其中， $a_k$ 是余弦项（表示偶数对称部分）， $b_k$ 是正弦项（表示奇数对称部分）。

偶数对称部分的捕捉

偶数对称部分 $x_{\text{even}}(t)$ 只能通过余弦函数来捕捉，因为余弦函数本身是偶函数。用数学公式表示：

$x_{\text{even}}(t) = \sum_{k} a_k \cos(\omega_k t)$

如果仅使用正弦函数：

$\sum_{k} b_k \sin(\omega_k t)$

那么我们得到的只是信号的奇数对称部分，而信号的偶数对称部分无法被表示或重构。

例子：单独使用正弦或余弦的不足

假设我们有一个信号 x(t)，它是纯粹的偶函数，即：

$\cos(\omega_0 t)$

如果我们仅使用正弦函数来表示这个信号：

$\sum_{k} b_k \sin(\omega_k t)$

由于 $\cos(\omega_0 t)$ 是偶函数，而正弦函数都是奇函数，无法通过正弦函数来表示 $\cos(\omega_0 t)$ ，所以信号的偶数对称部分（整个信号）会被完全忽略。

结论

傅里叶变换使用正弦和余弦函数是因为它们的正交性、复数表示的简洁性、对实数信号的良好适应性，以及它们共同构成了一个完备的基函数集合。单独使用正弦或余弦函数无法充分分解信号的所有频率成分，从而无法实现信号的完整表示和重构。

3. 频谱泄露

频谱泄露（Spectral Leakage）是信号处理和频谱分析中的一个常见现象，它通常在对信号进行离散傅里叶变换（DFT）或快速傅里叶变换（FFT）时出现。频谱泄露指的是信号的频谱成分在频率域中扩散到相邻的频率分量上，从而导致频谱分析结果的不准确。

频谱泄露的原因

频谱泄露主要是由于对信号进行截断或窗口化处理造成的。具体原因如下：

DFT的周期性假设：
DFT和FFT假设输入信号是一个周期信号，即信号在时间域上无限重复。在这种假设下，如果信号在截断点（即信号的开始和结束点）处不连续，这种不连续性会被视为信号中的高频成分。
不连续性引入高频成分：
当信号在截断点处不连续时，相当于在信号中引入了一个突变。根据傅里叶分析的原理，一个突变或不连续点在频域中会引入广泛的频率成分，特别是高频成分。这些高频成分会扩散到整个频谱上，导致频谱泄露。
信号截断：
在实际应用中，我们通常对有限长度的信号进行傅里叶变换。截断信号相当于将信号与一个矩形窗口相乘，而矩形窗口在频域中的表现是一个sinc函数 $\text{sinc}(f) = \frac{\sin(\pi f)}{\pi f}$ 。sinc函数的主瓣很宽，并且有许多旁瓣，这会导致频谱成分扩散到相邻的频率分量上。从计算角度看，在频域上，这相当于原信号的频谱 𝑋(𝑓)不得不与矩形窗的频谱（即sinc函数）进行卷积。

频谱泄露的表现

频谱泄露的主要表现是原本集中在某一频率上的能量扩散到其他频率上，使得频谱图上出现不希望看到的频率成分。这会使得频谱分析结果变得模糊，难以准确识别信号的频率成分。

减少频谱泄露的方法

为了减少频谱泄露，可以采取以下几种方法：

应用窗口函数：使用合适的窗口函数（如汉宁窗、汉明窗、布莱克曼窗等）对信号进行加窗处理。窗口函数的选择可以减少旁瓣的影响，从而减少频谱泄露。窗口函数在时间域中对信号进行加权，使得信号在截断点处平滑过渡。
增加信号长度：通过增加信号的采样长度，可以减少截断效应，从而降低频谱泄露的影响。
零填充（Zero Padding）：在信号末尾添加零值，使得信号长度增加，这可以提高频谱分辨率，使得频域表示更为精细，从而视觉上减少频谱泄露。从而使频谱泄露的影响更容易被识别和处理。

总结

频谱泄露是由于信号截断和不匹配的周期性导致的频谱成分扩散现象。通过使用窗口函数、增加信号长度和零填充等方法，可以有效减少频谱泄露的影响，从而提高频谱分析的准确性。

4. 增加信号长度缓解频谱泄露的原因是什么？

通过增加信号的采样长度，可以减少截断效应的原因有以下几个方面：

1. 提高频率分辨率

增加信号的采样长度 (N) 会直接提高离散傅里叶变换（DFT）的频率分辨率。频率分辨率定义为采样频率 (f_s) 除以信号长度 (N)，即
$\Delta f = \frac{f_s}{N}$
更高的频率分辨率意味着频域中频率点的间隔更小，可以更准确地表示信号的频率成分。这样，频谱泄露的效果会被减弱，因为每个频率成分能够被更精确地定位，不会出现过多的泄露现象。

2. 平滑信号过渡

当信号长度增加时，信号在时域上变得更长，再结合加窗，这通常会使得信号的过渡更加平滑。减少急剧变化，进而减少频谱泄露。

3. 零填充

即使实际信号长度不能增加，通过在信号末尾添加零（零填充），可以增加信号的有效长度。这不会改变信号的实际频谱，但会提高频率分辨率，使得频域表示更加精细。零填充后的频谱能够更好地展示信号的主要频率成分，并减少视觉上的频谱泄露。

从DFT计算公式看角度看，补零导致分母N增加，使得傅里叶变换过程中用到的一系列正交基函数的频率变化量更加精细致密。（补零就是逼着算法，或程序增加一些进行内积计算的正交基函数的数量，这些填充的0本质上没有参与计算，因为0乘对应的基函数的点的结果还是零，最后会与其他非零结果加和，反映该频点的最终频率幅值情况）。这就是增加信号长度导致频谱分辨率提高的本质原因。仅仅与长度的增加有关，而与具体长度增加的原因，比如填充是0，还是1，还是直接增加有效信号的长度没有关系。
但具体填充0，还是1，影响的是对实际信号信息的改变，比如填充1，很大可能改变了信号的能量分布，并加重了截断效应，导致频谱泄露效应显著增加，最终改变了频谱分布。
$\sum_{n=0}^{N-1} x[n] \left[\cos\left(\frac{2\pi kn}{N}\right) - j \sin\left(\frac{2\pi kn}{N}\right)\right]$

总结

增加信号采样长度（包括实际增加和零填充）可以提高频率分辨率、减少窗口效应带来的影响，并使信号过渡更平滑（结合加窗），从而有效减少频谱泄露。这对于精确的频域分析和信号处理具有重要意义。

5. 傅里叶变换结果的对称性

实信号的傅里叶变换结果具有共轭对称性，这一特性源于傅里叶变换的数学性质。

实部对称：实信号的傅里叶变换的实部是偶函数，即 $\Re\{X(f)\} = \Re\{X(-f)\}$ 。
虚部反对称：实信号的傅里叶变换的虚部是奇函数，即 $\Im\{X(f)\} = -\Im\{X(-f)\}$ 。
幅值对称：实信号的傅里叶变换的幅值是偶函数，即 $∣ X (f) ∣ = ∣ X (- f) ∣$ 。
相位反对称：实信号的傅里叶变换的相位是奇函数，即 $\arg(X(f)) = -\arg(X(-f))$ 。

这种对称性对于信号处理和频域分析非常重要，因为它简化了频谱分析，使得我们只需要分析正频率部分即可了解整个频谱。

6.快速傅里叶变换

快速傅里叶变换（FFT）利用信号的对称性和周期性，通过递归分解离散傅里叶变换（DFT），显著减少了计算量。以下是详细解释：

信号的对称性和周期性

对称性

傅里叶变换中，有以下对称性：

共轭对称性：
如果输入信号 $x [n]$ 是实信号，则其傅里叶变换 $X [k]$ 满足共轭对称性，即：
$X[k] = X[N-k]^*$
其中， $X[k]^*$ 表示 $X [k]$ 的复共轭。
偶奇对称性：
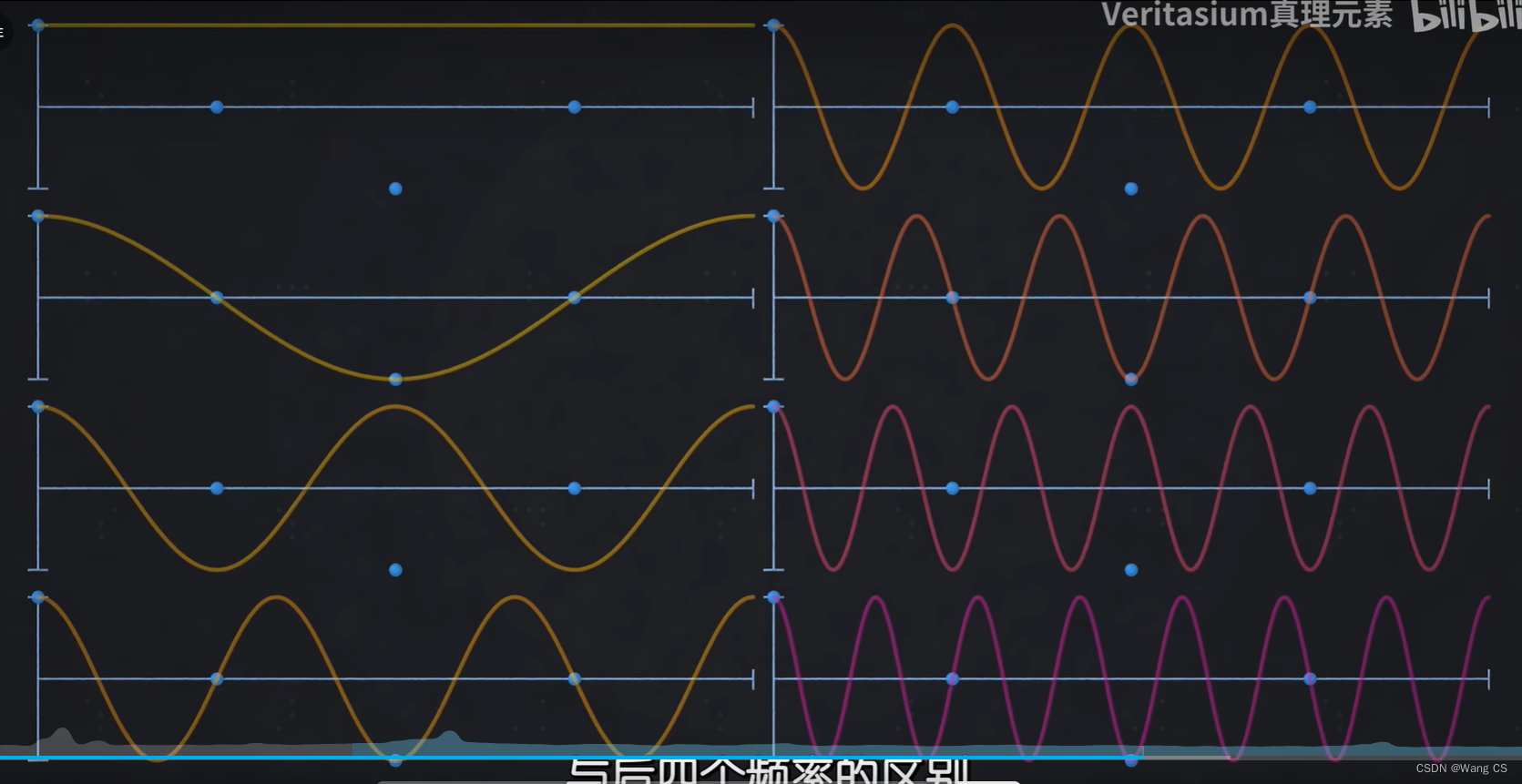
傅里叶变换中，对偶数和奇数索引位置的频谱分量可以利用对称性进行简化计算。以余弦函数为例，对于偶数索引，前一半的频率与后一半的频率有相同的余弦值。所以只需要计算前一半频率的余弦值就可以了。对于奇数索引和正弦函数，也有同样的规律，所以，fft可以不断的按照索引的奇偶性对数据进行划分计算。

周期性

DFT 的一个重要性质是其输出频谱是周期性的，周期为 $N$ 。即：
$X [k + N] = X [k]$

Cooley-Tukey 算法

FFT 中最常用的算法是 Cooley-Tukey 算法，它通过递归分解 DFT，利用上述对称性和周期性，显著减少了计算复杂度。其基本步骤如下：

分解

将长度为 $N$ 的信号 $x [n]$ 分成两个长度为 $N /2$ 的子信号：
- 偶数索引的样本： $x_e[n] = x[2n]$
- 奇数索引的样本： $x_o[n] = x[2n+1]$
对这两个子信号分别计算 DFT，得到两个长度为 $N /2$ 的频谱分量。

合并

利用递归计算得到的子信号的频谱，合并得到原始信号的频谱。具体来说：
$X[k] = X_e[k] + W_N^k X_o[k]$
$X[k+N/2] = X_e[k] - W_N^k X_o[k]$
其中， $W_N = e^{-j \frac{2\pi}{N}}$ 是旋转因子。
由于频谱是周期性的，只需计算一半的频谱分量，其余分量可通过共轭对称性得到。