一、线性判别分析LDA
线性判别分析是一种经典的线性学习方法,在二分类问题上最早是Fisher提出的,亦称为Fisher判别分析。
Fisher判别分析是一种用于降维和分类的统计方法,旨在找到可以最好区分不同类别的特征。它基于类内方差和类间方差的比值来选择最佳的投影方向,从而实现数据的最佳分类
思想:将训练集的样本投影到一条直线上,使得正类和反类投影在直线上的距离尽可能的分开。当测试集的样本被投影到直线上的时候,通过观察他的位置就可以知道该测试集的样本属于哪一类。
示意图

给定一个数据集D={xi,yi},Xi,μi,Σi分别表示例数集合,均值向量、协方差矩阵
投影之后再直线上的两类样本的中心点就是wTμ0和wTμ1,协方差:wTΣ0w,wTΣ1w
因为投影改变了数据的分布,所以协方差会随之改变。
就像我们之前讲到了,希望他们同类别的更接近,不同类别的就远离。其实就是最大化类中心之间的距离,最小化他们的协方差。这两个我们同时考虑的话。
将其定义为:


①类内散度矩阵
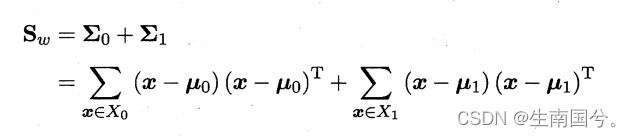
②类间散度矩阵
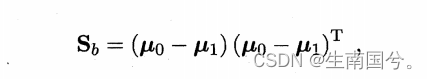
现在LDA就想要最大化目标Sb和Sw。
也叫做Sb与Sw的‘广义瑞利商’
如何确定w?
先介绍一下拉格朗日乘子法
我的理解就是:有变量,以及对于发原函数,有约束,求偏导,即求最优解

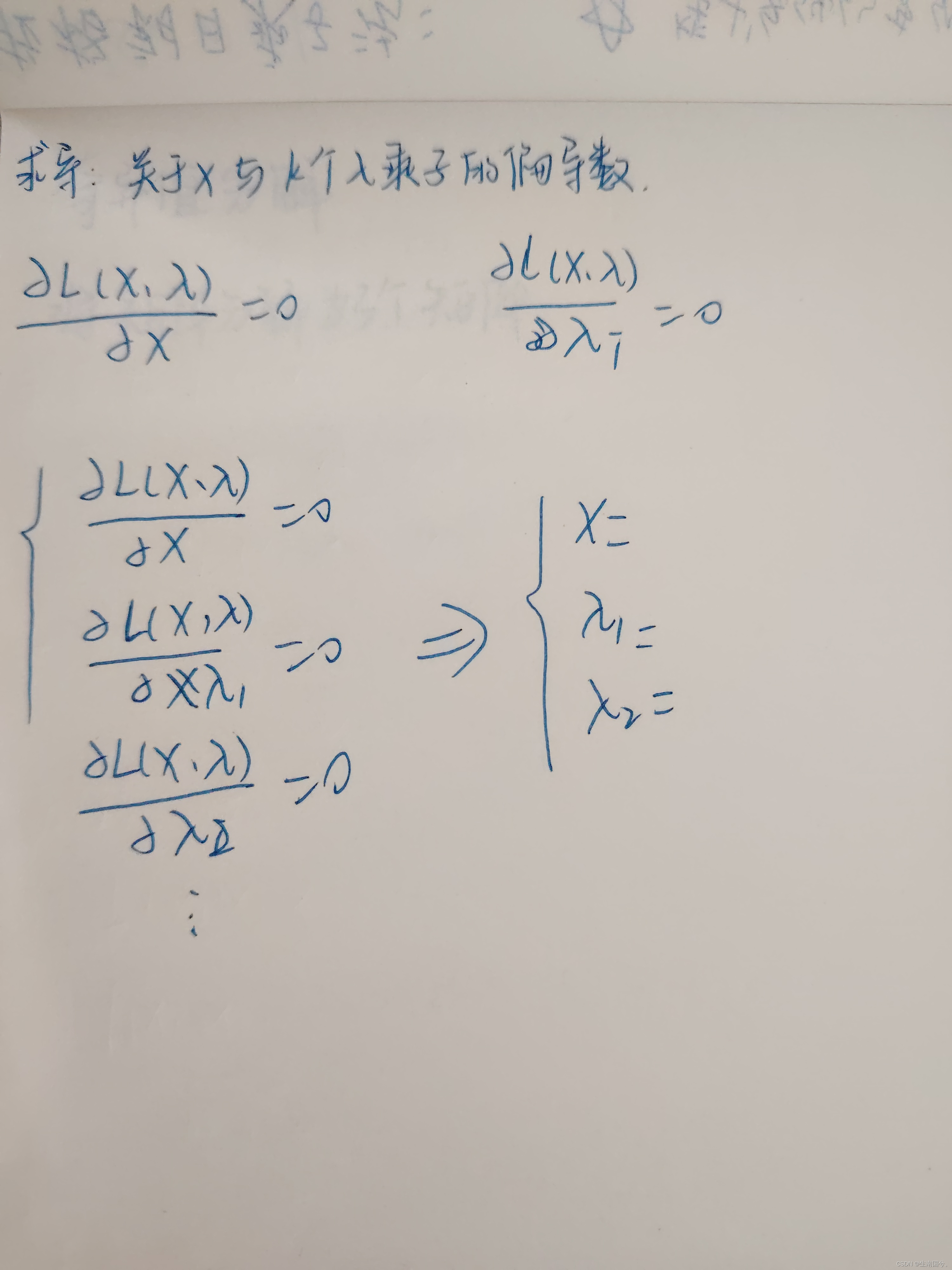
下面是对w的求解


在求解Sw的时候会使用到奇异值的分解
对于奇异值分解不太理解的可以参考这个
降维算法之奇异值分解SVD:7000字长文,看这一篇就够了!_奇异值分解降维-CSDN博客
二、多分类LDA
新定义了一个St,全局散度矩阵
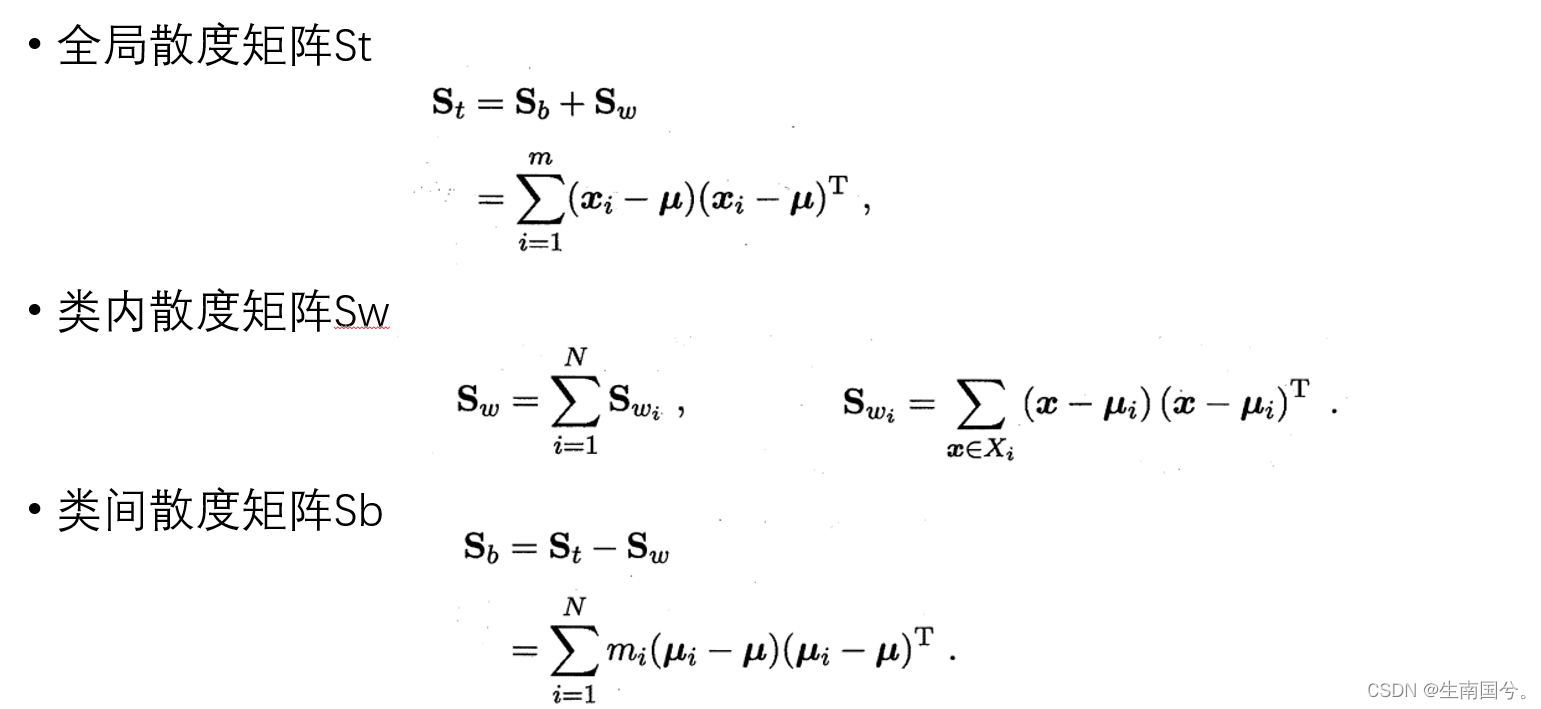
同样的要求解W
这里采用的是优化目标
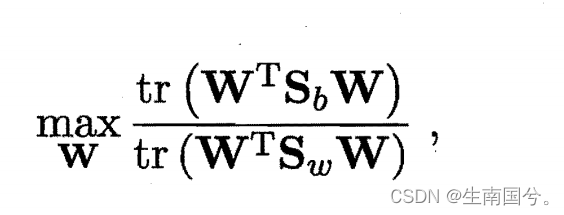
tr(·):代表矩阵的迹,是矩阵的主对角线上元素的总和。
对于多分类LDA的话就是将N个类别的投影到N-1个维度上,实现一个降维
因此,被视为一种经典的降维技术。
三、多分类学习
利用2分类策略解决多分类问题。
多分类学习的基本思路就是“拆解法“。最经典的有三种:一对一(O vs O),一对多(O vs R),多对多(M vs M).讲到这里,说不定你可以想到之前我们学过的也是类似分割的方法,对于模型评估那一块:有留出法、K折交叉验证法、自助法。
3.1 O vs O
将N个类别两两配对,看作排列组合就是,那么就会产生N(N-1)/2个二分类任务。
最终得到N(N-1)/2个分类结果,最终结果通过投票产生,即把预测的最多的类别作为最终分类结果
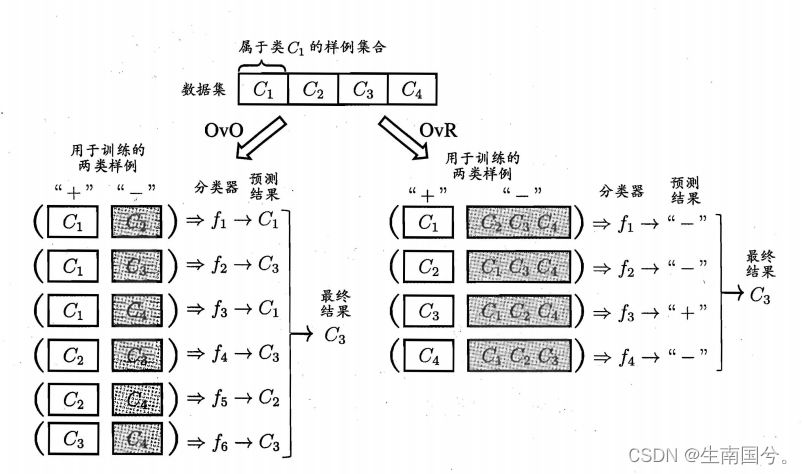
3.2 O vs R
将每一个类的样例作为正例,所有其他类的样例作为反类,训练N个分类器,在测试时若有一个分类器预测为正类,则对应的类别标记作为最终的分类结果。丢进去一个样本,若有多个分类器预测为正类,则通常考虑分类器的阈值置信度,选择置信度最大的类别标记作为分类结果。如上图。
其中,OVR需要训练N个分类器,但是OVO,却要训练N(N-1)/2个人分类器。因此一对一的存储开销和测试时间开销通常比一对多的更大,但是在训练的时候,一对多的每个分类器会使用全部的训练样本,而一对一的仅用到两个类的样本,因此在类别很多的时候,一对一的训练时间开销通常比一对多的 小。至于预测性能则却决于具体的数据分布,在多数情形下两者差不多。
3.3 M vs M
是每次将若干个类作为正类,若干个类作为反类。
但是多对多的正类和反类必须要有特殊的设计、不能随意的选取,在这里我们就介绍一种技术
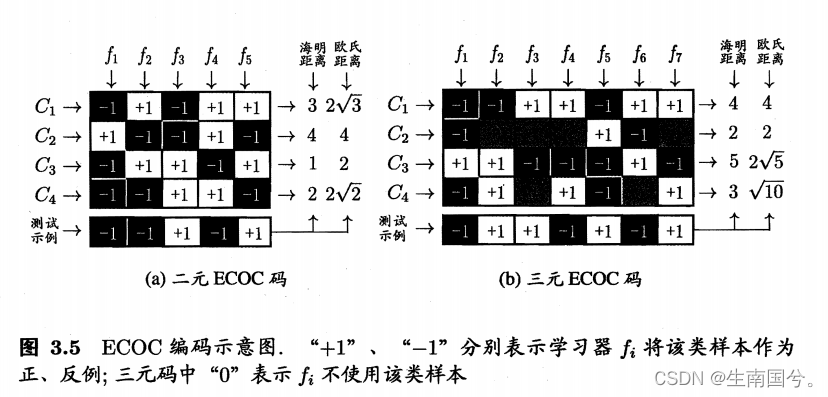
纠错输出码(ECOC)
第一步:编码:
对N个类别做M次划分,每次划分将一部分类别作为正类,一部分作为反类,从而形成一个二分类发训练集,一共产生M个训练集,可以训练出M个分类器
第二部:解码:
M个分类器分别对测试样本进行预测,这些预测标记组成一个编码,将这个预测编码与每个类别各自的编码进行比较,放回其中距离最小的类别作为最终预测结果
类别划分通过“编码矩阵“指定,编码矩阵有多种形式,常见的主要有——二元编码、三元编码前者将每个类别分别指定为正类和反类,后者在正类和反类之外,还指定了一个停用类。