CGS与MGS的矩阵正交化-C语言实现

news2025/1/13 13:20:11

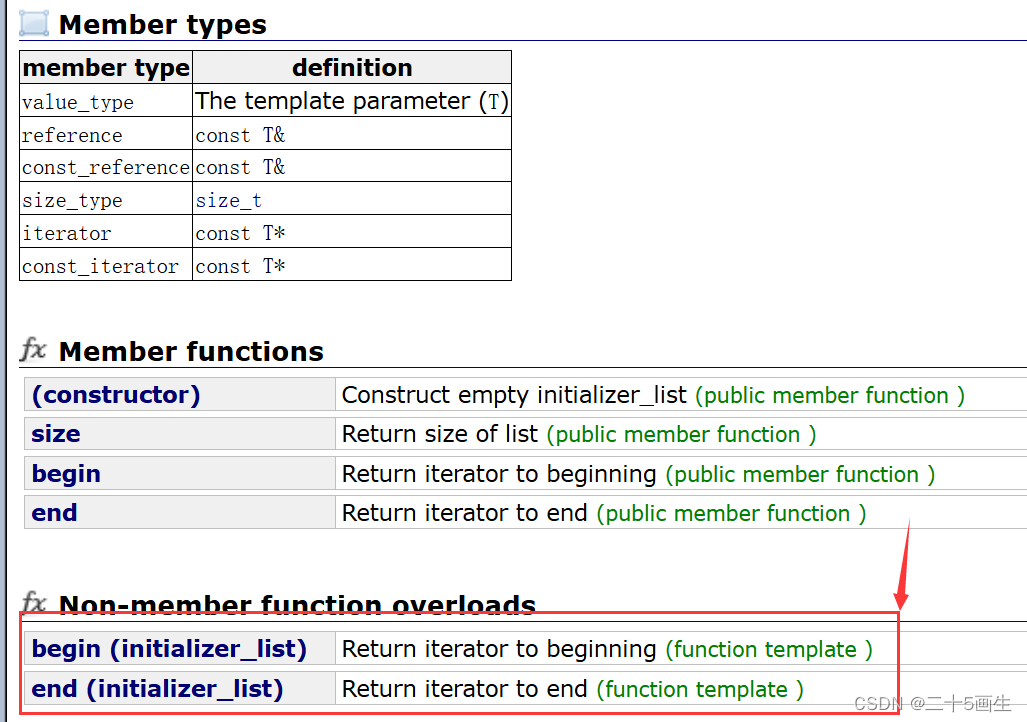
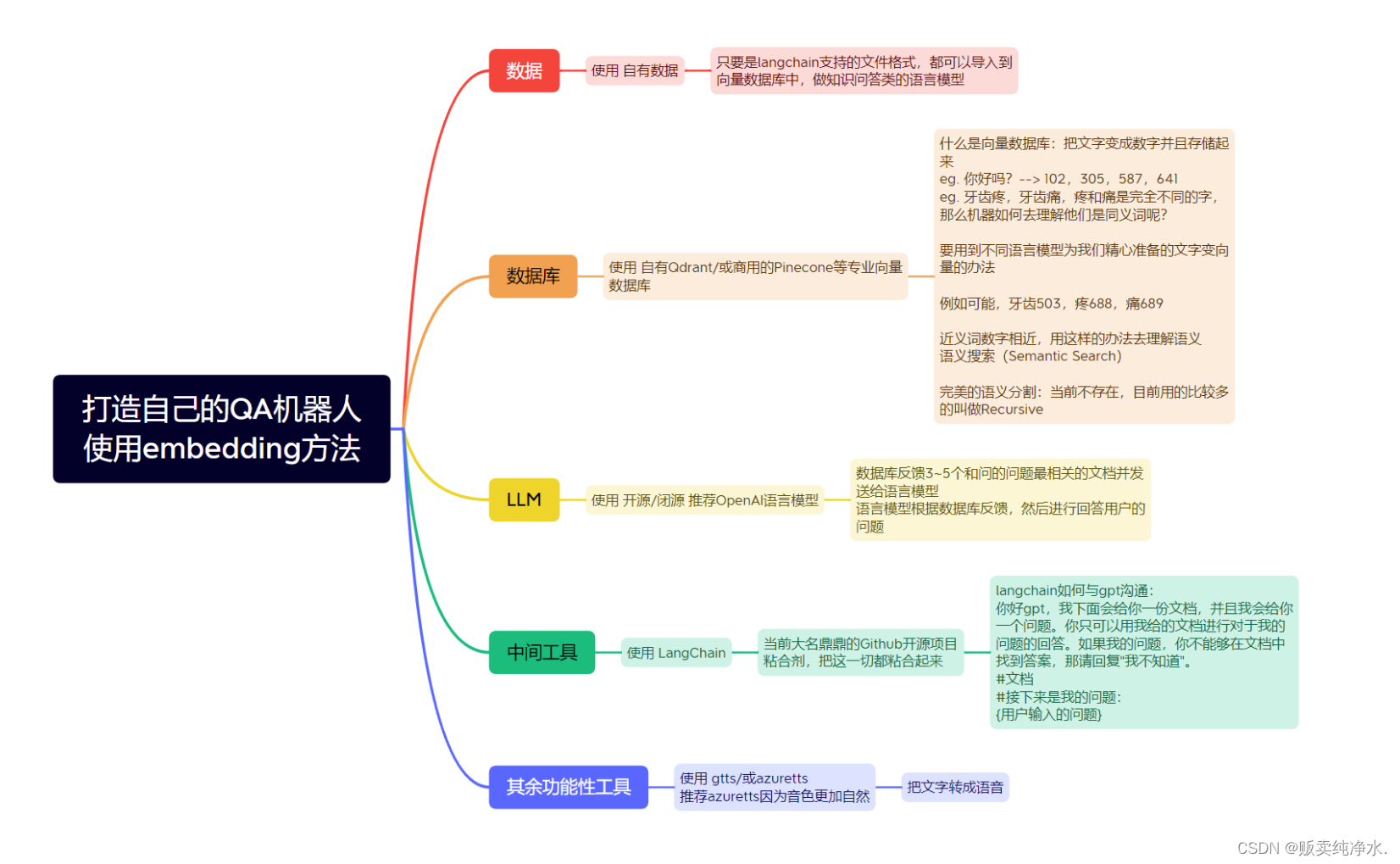
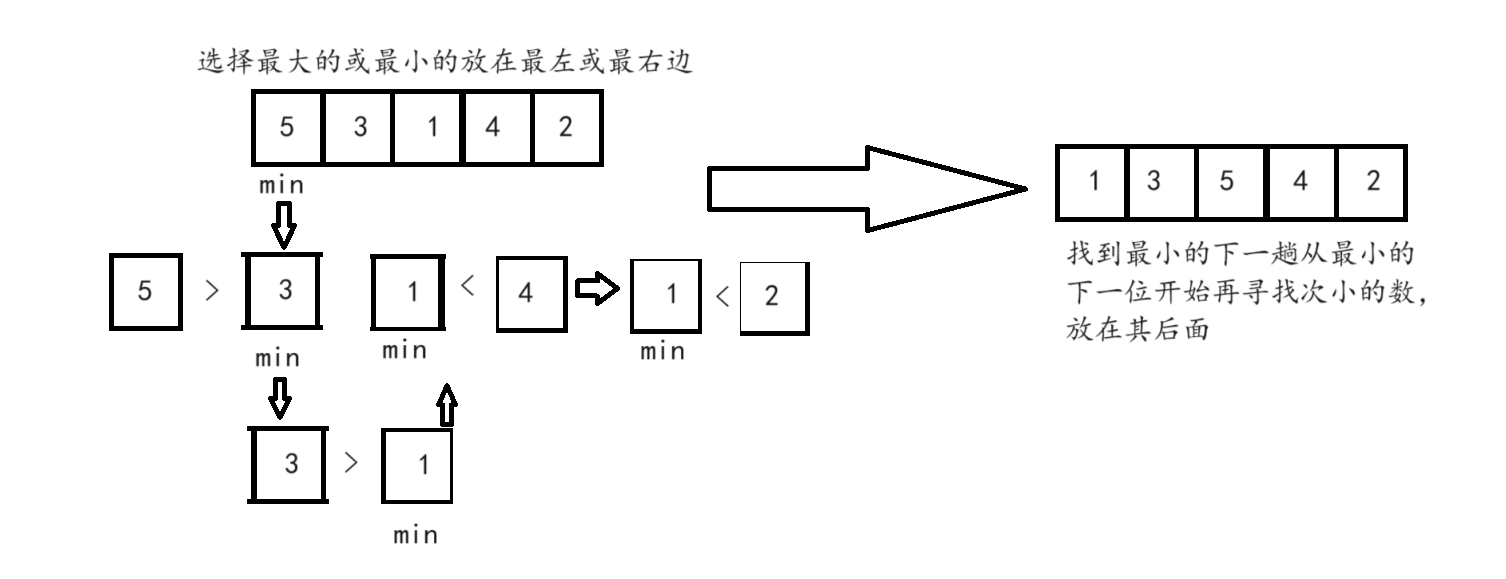
格拉姆-施密特正交化和改进的格拉姆-施密特正交化

格拉姆-施密特正交化CGS

数学公式

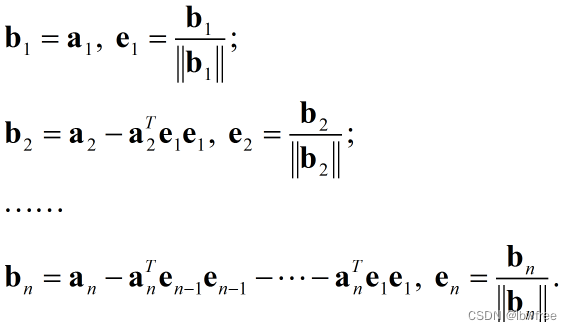
代码实现：

过程版

矩阵运算实现的难点在于每次运算都是一个向量，需要for循环进行，会带来运算时在代码中的复杂，进而难以理解代码的过程

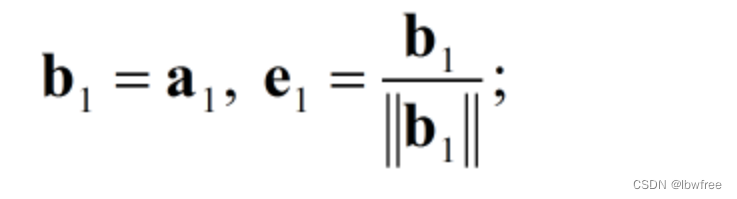
Q矩阵是{e...}  R矩阵是上三角矩阵 
Q[0] = A[0];   // -> b1 = a1
R[0][0] = norm(Q[0], m); //-> ||b1||
Q[0] =A[0] / R[0][0];    //-> b1/||b1||

先求 $a_{2}^{T}e_{1}$ R[1][2] = dotProduct(A[i], Q[j], m);

再用 Q[2] = A[2]; //这样可以使用迭代去求b2

R[j][i] = dotProduct(A[i], Q[j], m); // -> a2Te1

Q[i][k] = A[i][k];   //方便下一般实现循环递归减
Q[i][k] -=  R[j][i]*Q[j][k];   //用于递归实现 bn = an - anTen-1en-1-...

R[i][i] = norm(Q[i], m);// -> ||b1||
Q[i][k] /= R[i][i];    //-> b1/||b1||

纯净版

void cgs(double** A, int m, int n, double** Q, double** R) {
   
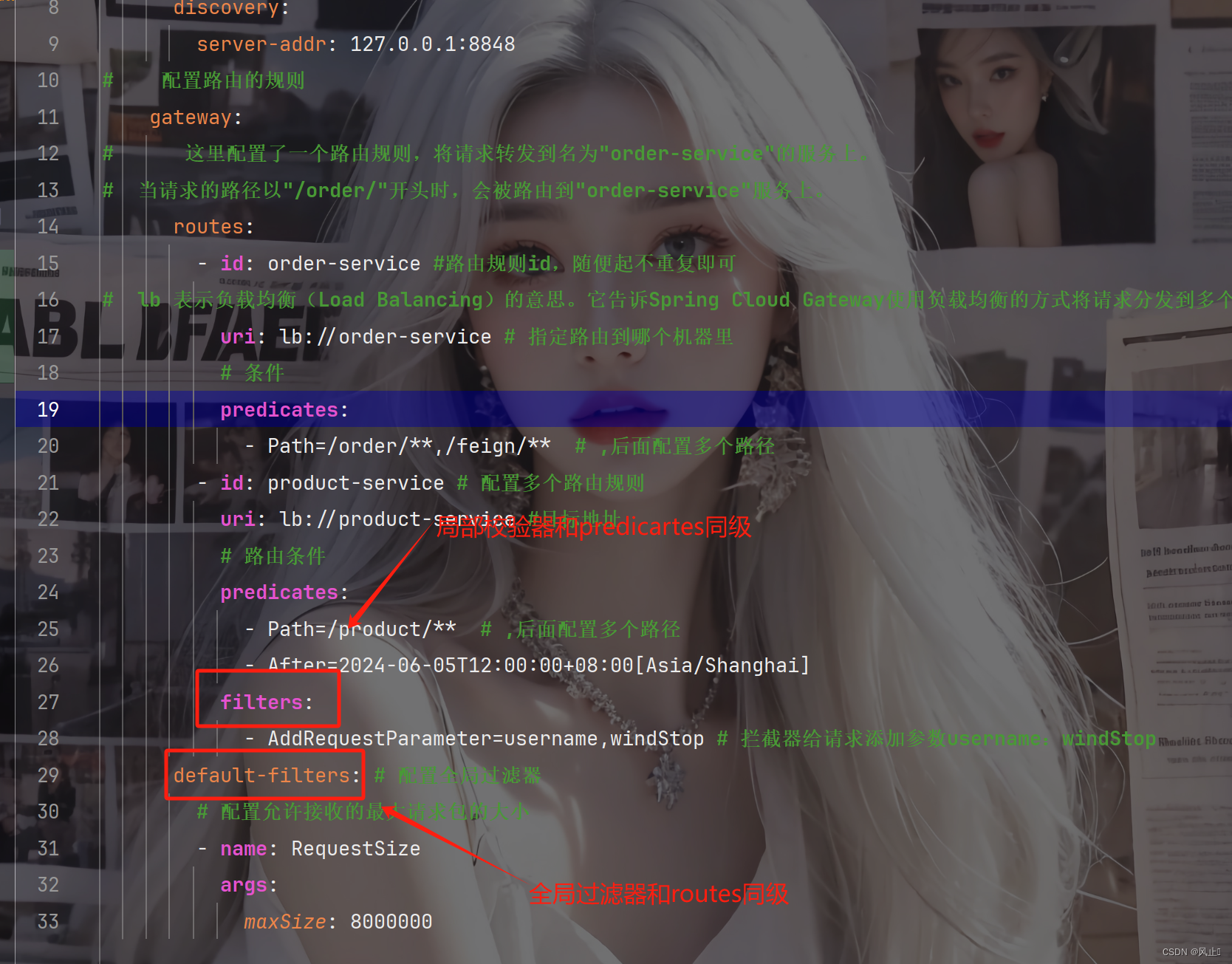
    if (n>=1)
    {
        R[0][0] = norm(A[0], m);
        for (int k = 0; k < m; k++) {
            Q[0][k] =A[0][k]/ R[0][0];
        }
    }
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < i; j++) {
            R[j][i] = dotProduct(A[i], Q[j], m);
        }
        for (int k = 0; k < m; k++)
        {
           Q[i][k] = A[i][k];
        }
        for (int j = 0; j < i; j++) {
            for (int k = 0; k < m; k++) {
                Q[i][k] -=  R[j][i]*Q[j][k];
            }
        }
        R[i][i] = norm(Q[i], m);
        for (int k = 0; k < m; k++) {
            Q[i][k] /= R[i][i];
        }
    }
}

改进的格拉姆-施密特正交化MGS

数学公式

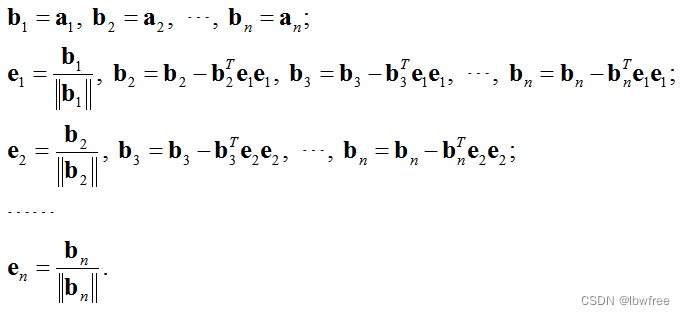
在于先求e 每次都对全部b进行运算

代码实现

过程版

for (int i = 0; i < m; i++)

{

Q[i]= A[i];

}

for (int i = 0; i < m; i++)
{
   for (int j = 0; j < n; j++)
   {
       Q[i][j] = A[i][j];
   }
}

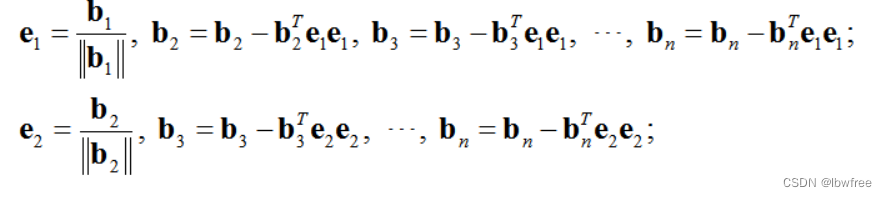
R[i][i] = norm(Q[i], m);
for (int k = 0; k < m; k++) {
      Q[i][k] /= R[i][i];
}

先求 $b_{2}^{T}e_{1}$

 R[i][j] = dotProduct(Q[i], Q[j], m);

对每一个b仅需运算每一个循环都会少计算b1，b2,b3..bn所以j = i+1

 for (int j = i + 1; j < n; j++) {
     for (int k = 0; k < m; k++) {
        Q[j][k] -= Q[i][k] * R[i][j];
     }
 }

纯净版

void mgs(double** A, int m, int n, double** Q, double** R) {
    for (int i = 0; i < m; i++)
    {
        for (int j = 0; j < n; j++)
        {
           Q[i][j] = A[i][j];
        }
    }
    for (int i = 0; i < n; i++) {
        R[i][i] = norm(Q[i], m);
        for (int k = 0; k < m; k++) {
            Q[i][k] /= R[i][i];
        }
        // 计算 R元素 b2Tei b3Tei...  Q[i]=e[i]
        for (int j = i + 1; j < n; j++) {
            R[i][j] = dotProduct(Q[i], Q[j], m);
        }
        // 更新 Q
        for (int j = i + 1; j < n; j++) {
            for (int k = 0; k < m; k++) {
                Q[j][k] -= Q[i][k] * R[i][j];
            }
        }
    }
}