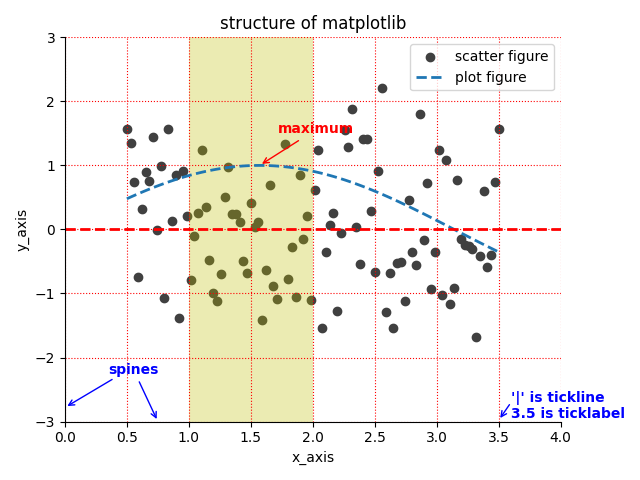
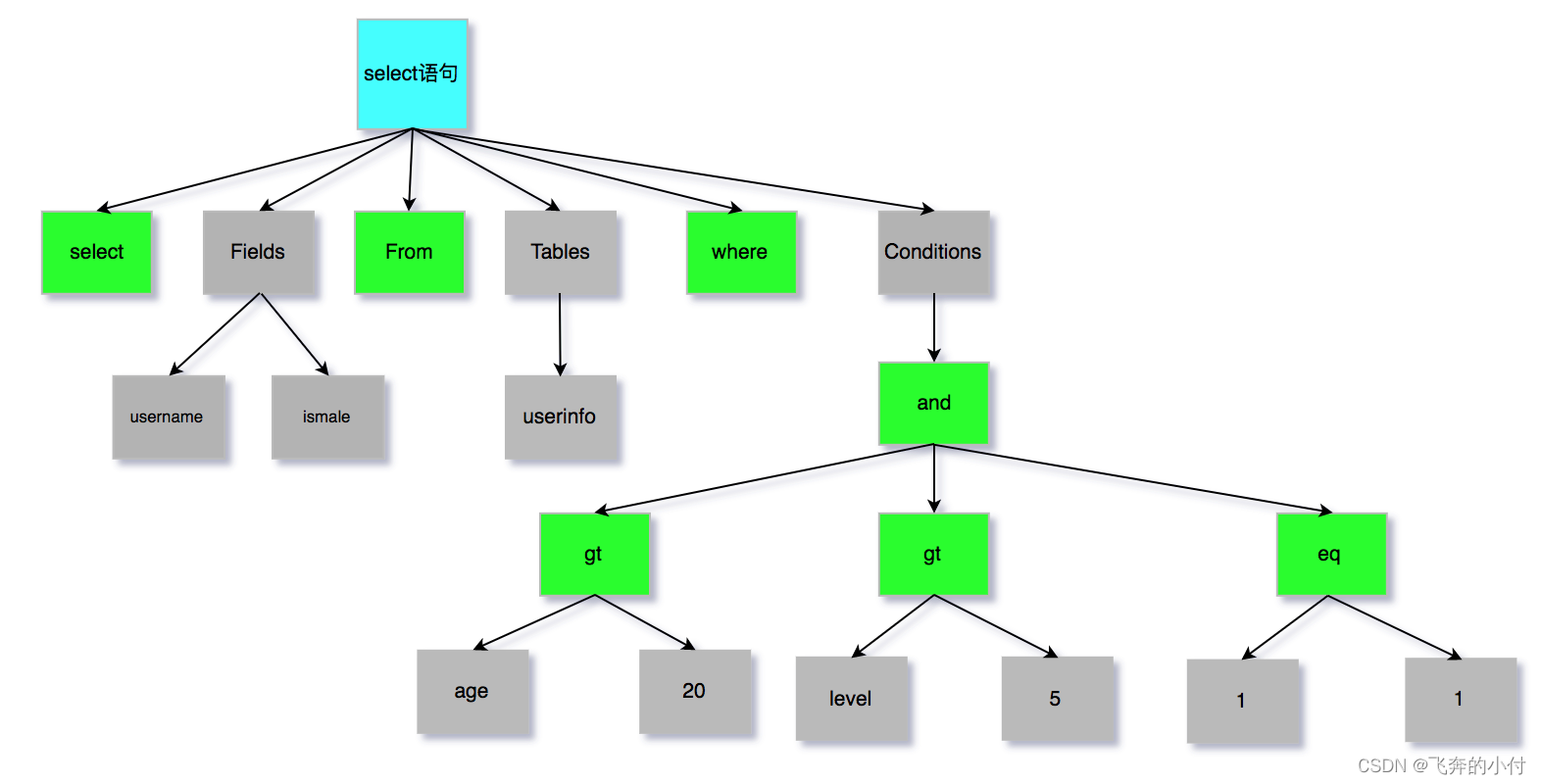
1 分支过程
1.1 工作原理
- 第一波疫情
- 假设一个人携带一种新的病毒,以独立的概率p将疾病传染给遇到的每一个人
- 假设这个人在感染期遇到了k个人
- ——>这k个人是该疾病传染的第一波
- 基于疾病是随机传染的,所以第一波中有些人会感染疾病,有些人则不会
- 第二波疫情
- 第一波疫情的每个人进入到人群中,又分别遇到k个不同的人
- 第二波疫情涉及的人数为
- 第二波疫情涉及的人数为
- 第一波疫情的每个人进入到人群中,又分别遇到k个不同的人
- 随后的疫情波
- 同理,每波传p个人
- 图b表示疾病传染性比较强的情况
- 图c表示疾病传染性比较弱的情况(第二波之后,就没有人感染了,疾病传播也就至此终结了)
- 疾病传播的分支过程模型实际上只有两种可能性:
- 达到某一疫情波没有人感染
- ——>疾病之后便消失
- 继续在每个疫情波中传染给某些人,这个过程持续下去
1.2 基本再生数R0
- 一个个体引发新病例的期望值
- 在分支过程模型中,每个人会接触k个人,每个人受感染的概率为p
- ——>基本再生数R0=pk
- 对于分支模型来说:
- 如果R0<1,那么疾病将在有限的疫情波之后,以概率1消失
- 疾病规模总体呈下降趋势,即使偶尔因为随机波动而增长
- 如果R0>1,那么疾病持续在每一波中,以大于0的概率至少传染给一个人
- 以大于0的概率持续传播,并不是绝对会持续传播
- ——>尽管很难掌握具体的疾病持续、消亡时间,但是基本再生数R0是刻画疾病传播力的非常有效的近似值
- 原来R0略低于1,如果此时传染概率p/接触人数k 略微增加,使得R0高于1
- ——>此时会造成疾病的突然爆发
- 反之亦然
- ——>减少疾病的传染概率、减少人们接触的人数,都会阻止、缓解疾病的传播速度
- 如果R0<1,那么疾病将在有限的疫情波之后,以概率1消失
- 如果不是分支模型的话,上述R0的结论不一定成立,比如下面这个非树形网络
- 我们记传染概率p为2/3
- 此时我们使用R0的定义:单一节点产生新病例数的期望值
- 每个受感染的节点连接着下一层的两个节点
- 每个节点被传染的概率是2/3
- —>单个节点产生的新病例数的期望值是4/3
- 此时R0>1,但这时疾病会在有限的时间内消失
- 每一层有四条边连接到下一层
- 每一条边没能传播疾病的概率是1/3
- 四条边都不传播疾病的概率是
- 这种疾病期望在81波后消失
疾病传播在不同的网络中可能有着显著不同的结果! 即使疾病的传染性等特征都一样。
2 SIR模型
2.1 疾病传播三阶段
- 易感(susceptible):患病之前,容易被感染的敏感期
- 传染(infection):感染疾病时。以一定概率把疾病传染给易感期的邻居
- 最初,一些节点处于传感阶段I,其他节点处于易感阶段S
- 每个进入I状态的节点在固定的时间t内具有传染性
- 在t的每一步,I状态的节点以p的概率将疾病传染给处于易感期S状态的邻居
- 移除(removed):经历了完整的传染期后,不再受感染
- 不具有传染性,也不会被传染。成为接触网络中的一个无效节点
2.2 SIR模型举例
- 粗黑的粉色节点表示I状态的节点
- 细黑的粉色节点表示R状态的节点

2.3 SIR模型的扩展
- 疾病在不同节点之间有不同的传染概率
- 节点v和w,他们之间的疾病传播概率为
。
- 大表示接触密切,容易传染;小表示接触比较稀少,不易传染
- 节点v和w,他们之间的疾病传播概率为
- 不同节点传染期的长度是随机的。。。
2.4 SIR模型的渗透表示 percolation
- 前面的SIR模型可以看成是一个动态模型(A先传了B,B再传C,C再传D。。。)
- 这个动态模型可以用一个静态模型等价表示
- 我们先看之前的动态SIR模型
- 一旦节点v被感染,成为了I阶段的节点,那么它有一次机会,以p的概率将疾病传给其易感邻居w
- ——>此时w是否被感染只与p有关,与v是什么时候被传染的没有关系
- ——>可以在一开始的时候根据概率p,算出每一条边是否可以传播疾病:可以传播的边是开放边,不能传播的边是阻塞边
- 节点v成为一个被传染的节点,当且仅当从某个最初传染节点到v点有一条全由开放边组成的路径
上述SIR模型的等价形式(静态渗透) ,可以看到被传播的点是X,V,R,W
3 SIS模型
- 在之前的SIR模型中,每个人最多只会得一次病;在SIS模型中,每个人可以多次患病
- 在SIS模型中,当节点结束传染状态后,他将直接循环回到易感状态中,并具备再次传染的条件

3.1 和SIR模型的关系
- SIR模型中,由于可接受传染的节点数量越来越少(最终都变成R状态的节点了),所以传染过程必然会在相对较少的步骤后结束
- 而对于SIS模型,由于一个节点可以多次反复地成为易感节点,所以传染过程可以持续一个很长的时间
3.1.1 将SIS模型变形为SIR模型
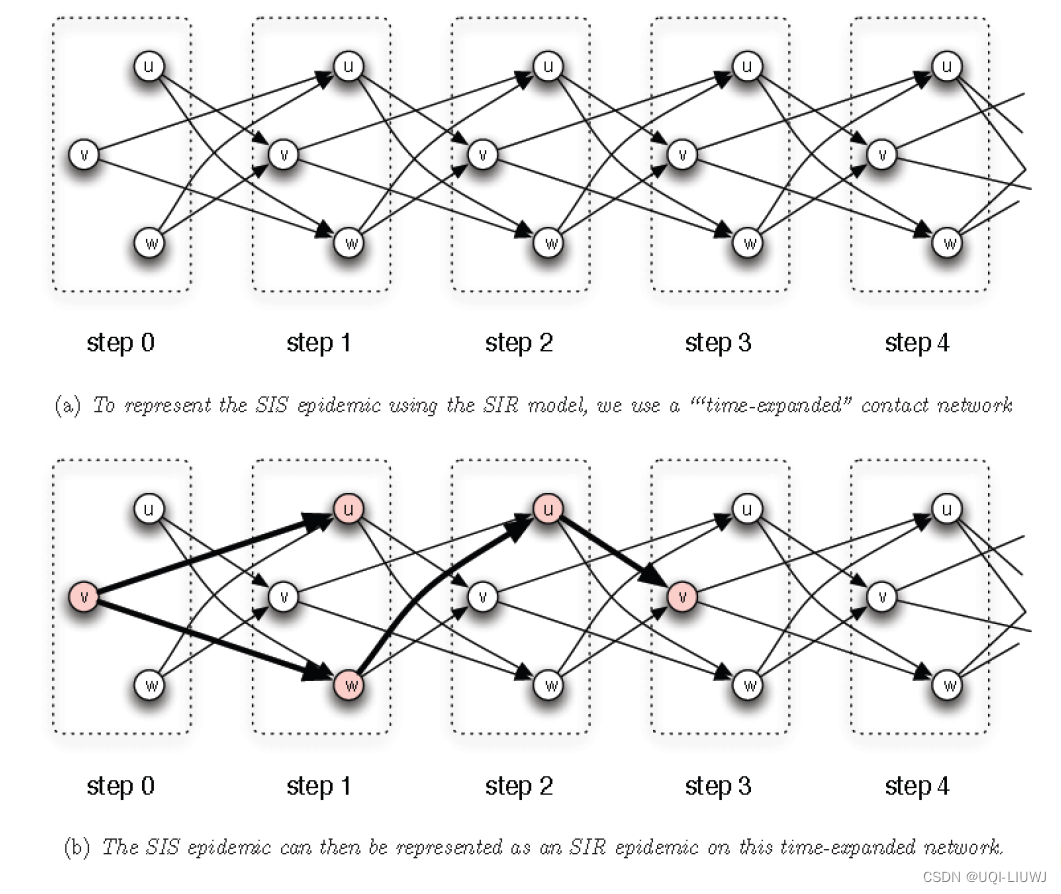
- 对一个SIS模型的节点V,我们创建(V,1),(V,2),(V,3),。。。。等节点副本
- ——>记形成的网络为时间扩展接触网络
- 原网络每条节点v到节点w的边,在时间扩展接触网络中,就是(V,t)到(W,t+1)的边
前面的SIS模型等价于如下的SIR模型:
4 SIRS流行病模型
I状态节点康复后,会短暂地进入R状态,然后回到S状态