“买卖股票的最佳时机” 系列——我来教你稳赚不亏~

news2025/1/12 20:37:14

目录

前言

一、买卖股票的最佳时机 ——>指定次数交易（1次）

1.1、dp定义

1.2、递推公式

1.3、遍历顺序

1.4、初始化

1.5、解题代码

二、买卖股票的最佳时机II ——>交易到结束

2.1、分析

2.2、解题代码

三、买股票的最佳时机III ——>指定次数交易（2次）

3.1、dp定义

3.2、递推公式

3.3、遍历顺序

3.4、初始化

3.5、解题代码

四、买股票的最佳时机IV ——>指定次数交易（k次）

4.1、分析 

4.2、解题代码

五、最佳买卖股票时机含冷冻期 ——>交易到结束（含冷冻期）

5.1、dp定义

5.2、递推公式

5.3、遍历顺序

5.4、初始化

5.5、解题代码

六、买卖股票的最佳时机含手续费 ——>交易到结束（含手续费）

6.1、分析

6.2、解题代码

小结

前言

        本篇题目虽然可以使用其他方法，如暴力枚举、贪心来解，但是只是针对特定场景的问题才可以，所以这里我将用动态规划的方法来教你，如何买股票，才能稳赚不亏！

一、买卖股票的最佳时机 ——>指定次数交易（1次）

题目描述：

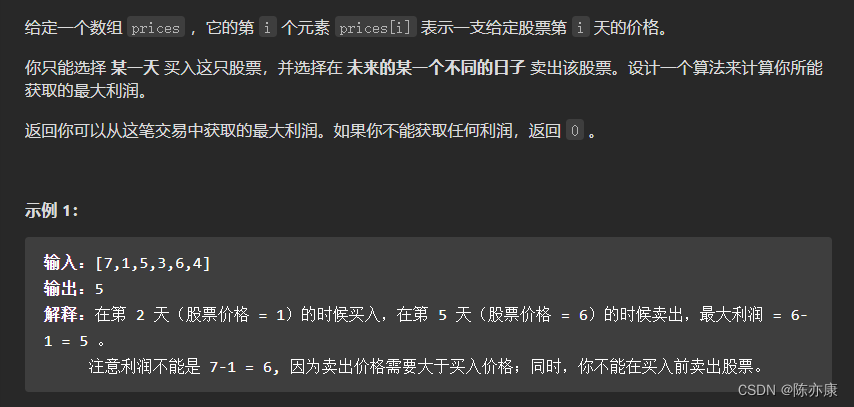
题目来源：121. 买卖股票的最佳时机

解题方法：

1.1、dp定义

分析：

第 i 天的股票无非就是两种状态，一种是这天持有股票dp[i][0]，另一种是这天不持有股票dp[i][1]，那么因该用一个二维数组表示第 i 天的状态（一维很难表示一天存在的两种状态）。

这里可能有人要问了：为什么不是定义为第i天买入股票，或是第i天卖出股票？

若是这样定义，就少了一些状态（保持卖出和买入状态），例如你定义第 i 天卖出股票，那么你第 i + 1 天的状态就是一个未知的状态（因为这一天还没有来临），当这i + 1天真的来临的时候你还要去定义它是卖出还是持有吗？一定要注意本题买卖股票只交易一次；

那么如果你是定义为“持有或不持有”，那么他状态就能延续下去，进行推导。（这是这类题解题的关键）

状态定义：

        dp[i][0]表示第 i 天持有股票的最大利润，dp[i][1]表示第 i 天不持有股票的最大利润，那么最终问题的解就是max(dp[len - 1][0], dp[len - 1][1])；（实际上这里的解因该是dp[len - 1][1]，因为你最后一天一定是一个股票不持有的状态，才是利润最大的！）

1.2、递推公式

分析：

dp[i][0]表示第 i 天持有股票，有两种情况：

1. 第 i 天才买的股票，所以第 i 天持有股票 --> -prices[i]。（这里直接是-prices[i]，是因为本题中买卖股票的交易只有一次，不存在i - 1天前交易获利了今天继续买股票的情况，也就是dp[i - 1][1] -prices[i]）

2. 前 i - 1 天中的某一天买的股票，所以第 i 天持有 --> dp[i - 1][0]。

dp[i][1]表示第i天不持有股票，有两种情况：

1. 之前一直持有股票，第 i 天才卖出股票，所以第 i 天不持有股票 --> dp[i - 1][0] + prices[i]。（前i - 1天持有股票的最大利润 + 第 i 天卖出所赚的利润）；

2. 前 i - 1天中的某一天卖出了，所以第 i 天不持有股票 --> dp[i - 1][1]。

状态转移方程：

dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);

dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);

1.3、遍历顺序

由上面的递推公式可以知道，第 i 天的状态是由前i - 1天的状态推导而来，所以是顺序遍历；

1.4、初始化

分析：

由递推公式中可以看出，每一个状态都需要依赖于前面的一个状态推导而来，那么一直往回推，推导根源就是dp[0][0]和dp[0][1]；

dp[0][0]表示第0天持有股票，那么就是第一个股票的价钱；

dp[0][1]表示都0天不持有股票，那么就是0；

初始化：

dp[0][0] = prices[0];

dp[0][1] = 0;

1.5、解题代码

class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp = new int[prices.length][2];
        //初始化
        dp[0][0] = -prices[0];//持有这个股票
        dp[0][1] = 0;//不持有这个股票
        for(int i = 1; i < prices.length; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return dp[prices.length - 1][1];
    }
}

二、买卖股票的最佳时机II ——>交易到结束

题目描述：

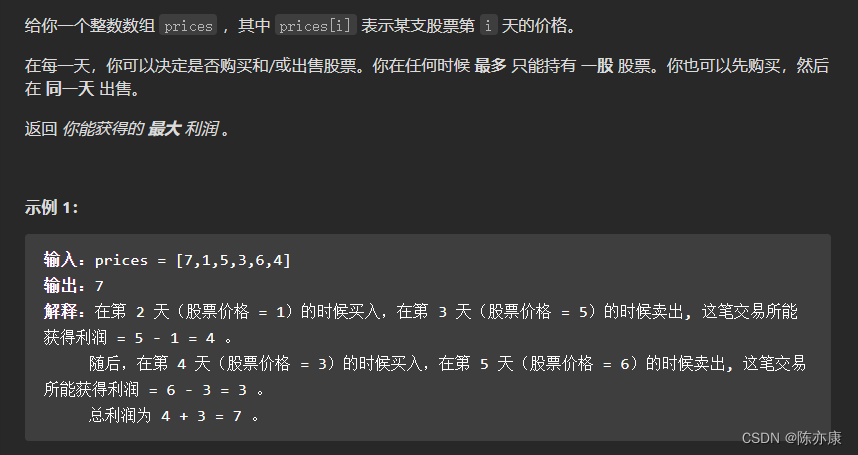
 题目来源：122. 买卖股票的最佳时机 II

2.1、分析

        与买股票的最佳时机I，唯一的差别就是本题买卖股票的次数可以是多次，那么不同点就是在状态转移方程上。

        实际上在那道题中，我就已经说明了，状态转移方程的区别，如果不太理解可以翻回去看看；

递推公式如下：

第i天持有股票：

dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);

第i天不持有股票：

dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);

2.2、解题代码

class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp = new int[prices.length][2];
        dp[0][0] = -prices[0];//持有
        dp[0][1] = 0;//不持有
        for(int i = 1; i < prices.length; i++) {
            //第i天持有股票
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            //第i天不持有股票
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return dp[prices.length - 1][1];
    }
}

三、买股票的最佳时机III ——>指定次数交易（2次）

题目描述：

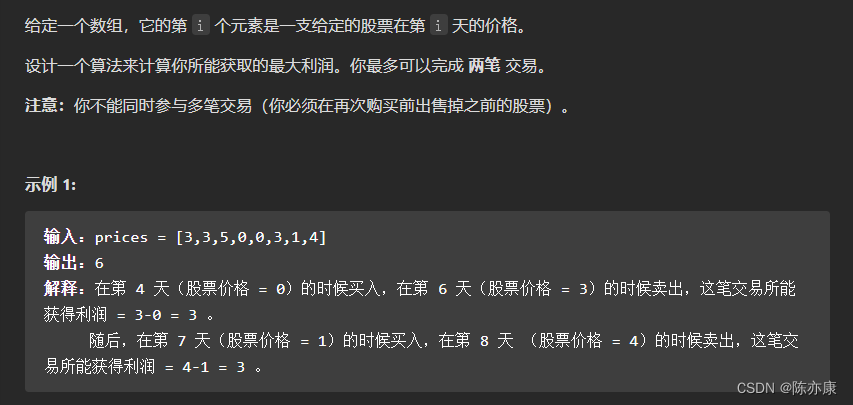
题目来源：123. 买卖股票的最佳时机 III

3.1、dp定义

        与前两道题唯一的区别是，本题买卖股票的交易只能进行两次，那么这里要定义的状态就需要多一些了；（为什么会像下方这样定义，在第一题中有详细分析）

dp[0][0]：什么都不操作。（这个状态可有可无，只是为了后面递推公式更加完整）；

dp[0][1]：第一次持有股票。

dp[0][2]：第一次不持有股票。

dp[0][3]：第二次持有股票。

dp[0][4]：第二次不持有股票。

3.2、递推公式

分析：

dp[i][0]：什么都不操作，那就可以表示为前一天的状态 --> dp[i - 1][0]。

dp[i][1]：可以是前i - 1就已经持有了第一次的股票 --> dp[i - 1][1]；也可以是今天才第一次买股票（那么前i - 1天一定是什么都没有做） --> dp[i - 1][0] - prices[i]。

dp[i][2]：可以是前i - 1天不持有第一次的股票 --> dp[i - 1][2]；也可以是前i - 1天持有第一次的股票，在第i天的时候才卖出 --> dp[i - 1][1] + prices[i]；

dp[i][3]：可以是前i - 1天就持有了第二次的股票 --> dp[i - 1][3]；也可以是前i - 1天不持有第二的股票，第i天才持有（那么一定是前i - 1天中的某一天已经不持有第一次的股票了） --> dp[i - 1][2] - prices[i]；

dp[i][4]：可以是前i - 1天不持有第二次的股票 --> dp[i - 1][4]；也可以是前i - 1天持有第二次的股票，接着第i天卖出第二次的股票 --> dp[i - 1][3] + prices[i]；

状态转移方程：

dp[i][0] = dp[i - 1][0];

dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);

dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);

dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);

dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);

3.3、遍历顺序

由上面的递推公式可以知道，第 i 天的状态是由前i - 1天的状态推导而来，所以是顺序遍历；

3.4、初始化

分析：

根据状态转移方程可以看出，每一个状态都是由前一个状态推出来的，一直往前推，也就是说，我们应该要初始化dp[0][0~4]；

注意：这里需要提前知道的一点是，题目中没有明确规定，“股票不能当天买入天卖出”，实际上，“这天什么都不干” 就等同于 “股票当天买入当天卖出”，她两的利润都是0，所以可以认为是一样的。（这对理解初始化至关重要）

解释：

dp[0][0]：第一天什么都不做，那么最大利润一定是0；

dp[0][1]：第一天第一次持有股票，那么一定是是第一天买入的的股票，也就是-prices[0]；

dp[0][2]：第一天第一次不持有股票，就是第一天什么都没做，也可以理解为“股票当天买入当天卖出”，最大利润就是0；

dp[0][3]：第一天第二次持有股票，可以理解为“这一天已经进行了一次买卖股票”，接着，又买了一次股票，所以利润就是-prices[0]；

dp[0][4]：第一天第二次不持有股票，可以理解为“这一天已经进行了一次买卖股票”，接着，并没有做任何操作，那么最大利润还是0；

初始化：

dp[0][0] = 0;//不操作

dp[0][1] = -prices[0];//第一次持有

dp[0][2] = 0;//第一次不持有

dp[0][3] = -prices[0];//第二次持有

dp[0][4] = 0;//第二次不持

3.5、解题代码

class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp = new int[prices.length][5];
        //初始化
        dp[0][0] = 0;//不操作
        dp[0][1] = -prices[0];//第一次持有
        dp[0][2] = 0;//第一次不持有
        dp[0][3] = -prices[0];//第二次持有
        dp[0][4] = 0;//第二次不持有
        for(int i = 1; i < prices.length; i++) {
            dp[i][0] = dp[i - 1][0];
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
            dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
        return dp[prices.length - 1][4];
    }
}

四、买股票的最佳时机IV ——>指定次数交易（k次）

题目描述：

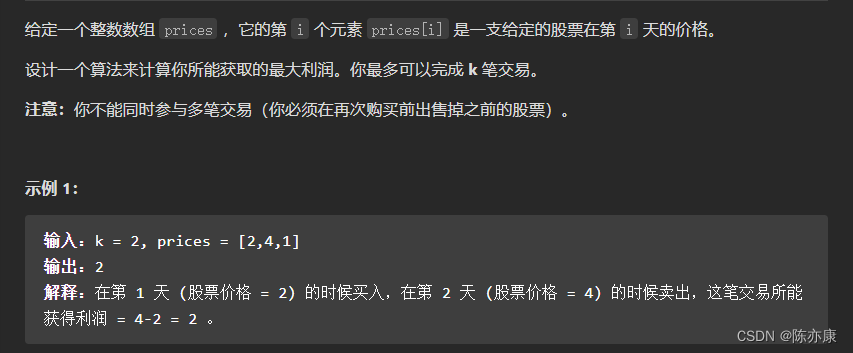
题目来源：188. 买卖股票的最佳时机 IV

4.1、分析 

本题就是 “买卖股票的最佳时机III” 的升级版，买卖股票的次数由2次变成了k次。

不难看出，本题虽有有了更多的状态，但dp数组的含义，状态转移方程，初始化是一样的；

因此，如果你理解了 “买卖股票的最佳时机III” 的题解，这道题是可以直接秒杀的；

4.2、解题代码

class Solution {
    public int maxProfit(int k, int[] prices) {
        int ans = 2 * k + 1;
        int[][] dp = new int[prices.length][ans];
        //初始化
        for(int i = 0; i < ans; i++) {
            dp[0][i] = i % 2 == 0 ? 0 : -prices[0];
        }
        //遍历
        for(int i = 1; i < prices.length; i++) {
            dp[i][0] = dp[i - 1][0];
            for(int j = 1; j < ans; j++) {
                if(j % 2 == 1) { //买入
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - 1] - prices[i]);
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - 1] + prices[i]);
                }
            }
        }
        return dp[prices.length - 1][ans - 1];
    }
}

五、最佳买卖股票时机含冷冻期 ——>交易到结束（含冷冻期）

题目描述：

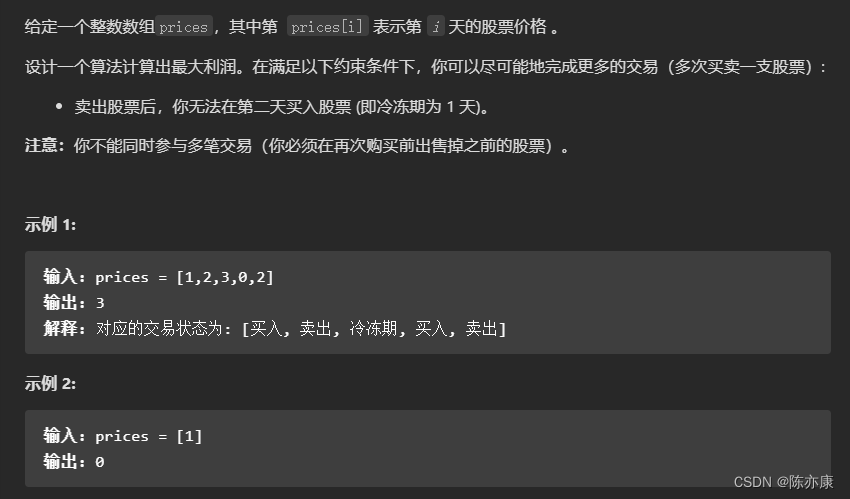
题目来源：309. 最佳买卖股票时机含冷冻期

5.1、dp定义

分析：

        以往的题我们都是拆分成 [持股，不持股] 两种状态，本题多了一个冷冻期状态，冷冻期是要求前一天必须为“当天卖出”状态，而我们的“不持股”状态（它表示从某一天卖出开始一直不持股持续到今天，具体是那一天开始不持股不知道！）无法准确描述它，因此，我们需要将“不持股”这个状态拆分成 “冷冻期后的不持股” 和 “当天卖出不持股”这两种状态。

dp定义：

dp[i][0]：持股 时所含的最大利润；

dp[i][1]：冷冻期后的不持股 时所含的最大利润；

dp[i][2]：当天卖出股票 时所含的最大利润；

dp[i][3]：冷冻期 时所含的最大利润；

5.2、递推公式

分析：

dp[i][0]：持股 有三种情况：

1.前i - 1天一直持股，今天延续这个状态；2.冷冻期后不持股，然后当天买入股票；3.前一天是冷冻期，今天买入股票。

dp[i][1]：冷冻期后的不持股 有两种情况：

1.前i - 1天一直是冷冻期后的不持股状态，今天延续这个状态；2.前一天就是冷冻期，今天就是冷冻期后的不持股状态。

dp[i][2]：当天卖出股票 只有一种情况：

1.前i - 1天持股，今天卖出。

dp[i][3]：冷冻期 只有一种情况：

1.前一天卖出股票。

状态转移方程：

dp[i][0] = Math.max(dp[i - 1][0], Math.max(dp[i - 1][1] - prices[i], dp[i - 1][3] - prices[i]));

dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][3]);

dp[i][2] = dp[i - 1][0] + prices[i];

dp[i][3] = dp[i - 1][2];

5.3、遍历顺序

由上面的递推公式可以知道，第 i 天的状态是由前i - 1天的状态推导而来，所以是顺序遍历；

5.4、初始化

Ps：这里分析思路和 “买卖股票的最佳时机III的方法是一样的”；

dp[0][0] = -prices[0];//持股

dp[0][1] = 0;//冷冻期后的不持股

dp[0][2] = 0;//当天卖出股票

dp[0][3] = 0;//冷冻期

5.5、解题代码

class Solution {
    public int maxProfit(int[] prices) {
        int len = prices.length;
        int[][] dp = new int[len][4];
        dp[0][0] = -prices[0];//持股
        dp[0][1] = 0;//冷冻期后的不持股
        dp[0][2] = 0;//当天卖出股票
        dp[0][3] = 0;//冷冻期
        for(int i = 1; i < len; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], Math.max(dp[i - 1][1] - prices[i], dp[i - 1][3] - prices[i]));
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][3]);
            dp[i][2] = dp[i - 1][0] + prices[i];
            dp[i][3] = dp[i - 1][2];
        }
        return Math.max(dp[len - 1][1], Math.max(dp[len - 1][2], dp[len - 1][3]));
    }
}

六、买卖股票的最佳时机含手续费 ——>交易到结束（含手续费）

题目描述：

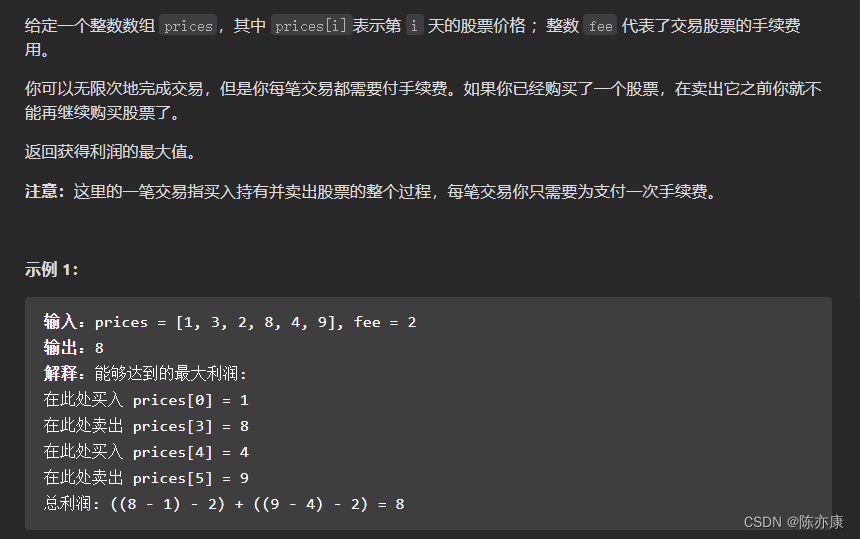
题目来源：714. 买卖股票的最佳时机含手续费 

6.1、分析

此题可以说是和 “买卖股票的最佳时机II” 几乎一模一样......

唯一的区别就是本题在每次买卖股票完后，都需要减掉一个手续费~

因此，如果你理解了 “买卖股票的最佳时机II” 的题解，这道题是可以直接秒杀的；

6.2、解题代码

class Solution {
    public int maxProfit(int[] prices, int fee) {
        int[][] dp = new int[prices.length][2];
        dp[0][0] = -prices[0];//持股
        dp[0][1] = 0;//不持股
        for(int i = 1; i < prices.length; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
        }
        return dp[prices.length - 1][1];
    }
}

小结

你学会怎么买股票了吗？（bushi）

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/179096.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【keepass】密码管理软件keepass的安全风险分析，如何在使用keepass的过程中避免泄露数据库信息和密码？

【keepass】密码管理软件keepass的安全风险分析，如何在使用keepass的过程中避免泄露数据库信息和密码？

一、安全风险分析 1.1 不正规的来源 如果你使用非官方渠道获得keepass软件或某些插件&#xff0c;那么你的密码管理从一开始就没有安全性可言。因为这玩意是开源的啊&#xff0c;如果对方“很懂”&#xff0c;只要往里面植入一些代码&#xff0c;让你的数据库文件和密钥在后台…
阅读更多...
react 项目 中 使用 Dllplugin 打包优化

react 项目 中 使用 Dllplugin 打包优化

webpack在build包的时候&#xff0c;有时候会遇到打包时间很长的问题&#xff0c;这里提供了一个解决方案&#xff0c;让打包如丝般顺滑~ 在用 Webpack 打包的时候&#xff0c;对于一些不经常更新的第三方库&#xff0c;比如 react&#xff0c;lodash&#xff0c;vue 我们希望…
阅读更多...
C语言基础知识（37）

C语言基础知识（37）

数组一维数组的定义&#xff1a;类型说明符 数组名【常量表达式】&#xff1b;先定义后引用&#xff1b;一维数组初始化时可以只对一部分元素初始化&#xff0c;在对全部数组元素初始化的时候可以部规定长度&#xff1b;但是若被定义的数组长度与提供的初始值不一样时&#xff…
阅读更多...
【MySQL】MySQL索引夺命连环问「持续更新中」

【MySQL】MySQL索引夺命连环问「持续更新中」

文章目录1. 使用MySQL索引的原因2. 索引的三种常见底层数据结构以及优缺点3. 索引的常见类型以及它是如何发挥作用的&#xff1f;4. MyISAM 和 InnoDB 实现 B 树索引方式的区别是什么&#xff1f;5. InnoDB 为什么设计 B 树索引&#xff1f;6. 什么是覆盖索引和索引下推&#x…
阅读更多...
【JavaSE专栏7】Java 常量、变量及其作用域

【JavaSE专栏7】Java 常量、变量及其作用域

作者主页&#xff1a;Designer 小郑 作者简介&#xff1a;Java全栈软件工程师一枚&#xff0c;来自浙江宁波&#xff0c;负责开发管理公司OA项目&#xff0c;专注软件前后端开发&#xff08;Vue、SpringBoot和微信小程序&#xff09;、系统定制、远程技术指导。CSDN学院、蓝桥云…
阅读更多...
Python论文绘图利器seaborn.lineplot

Python论文绘图利器seaborn.lineplot

Python论文绘图利器seaborn.lineplot 提示&#xff1a;前言 Python论文绘图利器seaborn.lineplot 提示&#xff1a;写完文章后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录Python论文绘图利器seaborn.lineplot前言一、导入包二、加载数据三…
阅读更多...
嵌入式桌面管理系统Matchbox

嵌入式桌面管理系统Matchbox

简介 Matchbox&#xff08;中文译名&#xff1b;火柴盒&#xff09;是X Window System的免费和开源Window Manager&#xff0c;它主要用于嵌入式系统。取名Matchbox&#xff0c;很形象的表明它只适用于屏幕只有火柴盒大小的设备。 buildroot 移植MatchBox session managermat…
阅读更多...
高斯秩变换 RankGauss 可能是比标准化/归一化更有效的连续值特征变换方法

高斯秩变换 RankGauss 可能是比标准化/归一化更有效的连续值特征变换方法

文章目录 一、前言二、关键原理三、总结CSDN 叶庭云：https://yetingyun.blog.csdn.net/ 一、前言 高斯秩变换是 Kaggle 竞赛大佬 Michael Jahrer（Grandmaster） 提出的一种新颖的特征变换方法，他称之为 RankGauss。类似归一化（MinMax）和标准化（Standardization）的作用，…
阅读更多...
帆软报表 V8 get_geo_json 任意文件读取漏洞

帆软报表 V8 get_geo_json 任意文件读取漏洞

帆软报表 V8 get_geo_json 任意文件读取漏洞 CNVD-2018-04757 1.漏洞介绍 FineReport报表软件是一款纯Java编写的&#xff0c;集数据展示(报表)和数据录入(表单)功能于一身的企业级web报表工具。 FineReport v8.0版本存在任意文件读取漏洞&#xff0c;攻击者可利用漏洞读取网…
阅读更多...
车载以太网 - 测试用例设计 - 头部信息检测 - 10

车载以太网 - 测试用例设计 - 头部信息检测 - 10

前面的篇幅已经把ISO 13400中DoIP软件协议规范部分进行详细的介绍说明，如果在文章中有哪些介绍的不充分或者不够详细，欢迎评论区留言讨论；接下来的文章主要介绍DoIP协议相关的测试用例设计，这也是一个测试工程师必备的重要技能之一，能否保证测试执行完成后，软件质量是达到…
阅读更多...
超级详解洛谷P4011 孤岛营救问题(bfs超难题)(保证看懂)

超级详解洛谷P4011 孤岛营救问题(bfs超难题)(保证看懂)

题目 说明 1944 年&#xff0c;特种兵麦克接到国防部的命令&#xff0c;要求立即赶赴太平洋上的一个孤岛&#xff0c;营救被敌军俘虏的大兵瑞恩。瑞恩被关押在一个迷宫里&#xff0c;迷宫地形复杂&#xff0c;但幸好麦克得到了迷宫的地形图。迷宫的外形是一个长方形&#xff…
阅读更多...
阿里“云开发“小程序(uniCould)

阿里“云开发“小程序(uniCould)

博主ps&#xff1a; 网上资料少的可怜&#xff0c;哎&#xff0c;腾讯云涨价了&#xff0c;论服务器&#xff0c;我肯定选的阿里&#xff0c;再着你们对比下unicould的报价就知道了&#xff0c;如果有钱就另当别论了。 所以这片博文&#xff0c;博主试过之后&#xff0c;先抛出…
阅读更多...
(day8) 自学Java——拼图小游戏

(day8) 自学Java——拼图小游戏

GUI(图形用户接口)&#xff0c;是指采用图形化的方式显示操作界面。 Java中包含两套完整体系&#xff1a;AWT包&#xff0c;Swing包 一.代码 package com.abc.ui;import javax.swing.*; import javax.swing.border.BevelBorder; import java.awt.event.ActionEvent; import ja…
阅读更多...
JavaEE day5 初识CSS 2

JavaEE day5 初识CSS 2

选择器 基本选择器&#xff1a;id选择器、类选择器、元素选择器 复合选择器&#xff1a;并列选择器、子孙选择器、孩子选择器 通配符选择器 *{.....} 任意元素&#xff1a;书写一些全局的规则时使用&#xff0c;就等于是一个全局都要遵守的规则 伪类选择器&#xff1a;针…
阅读更多...
Lab 3: Midterm Review

Lab 3: Midterm Review

Lab3 部分questionQ5&#xff1a;Its Always a Good PrimeQ6&#xff1a;Church numeralsQ5&#xff1a;It’s Always a Good Prime Implement div_by_primes_under, which takes in an integer nand returns an n-divisibility checker. An n-divisibility-checker is a funct…
阅读更多...
【蓝桥杯选拔赛真题35】python回文数升级 青少年组蓝桥杯python 选拔赛STEMA比赛真题解析

【蓝桥杯选拔赛真题35】python回文数升级 青少年组蓝桥杯python 选拔赛STEMA比赛真题解析

目录 python输出N除以3的商 一、题目要求 1、编程实现 2、输入输出
阅读更多...
二叉树22：二叉搜索树中的搜索

二叉树22：二叉搜索树中的搜索

主要是我自己刷题的一些记录过程。如果有错可以指出哦&#xff0c;大家一起进步。 转载代码随想录 原文链接&#xff1a; 代码随想录 leetcode链接&#xff1a;700. 二叉搜索树中的搜索 题目&#xff1a; 给定二叉搜索树&#xff08;BST&#xff09;的根节点 root 和一个整数…
阅读更多...
变量的了解

变量的了解

1、普通局部变量 -------------定义形式&#xff1a;在{}里面定义的 普通变量 叫做 普通局部变量 -------------作用范围&#xff1a;所在的 {} 复合语句之间有效 -------------生命周期&#xff1a;所在的 {} 复合语句之间有效 -------------存储区域&#xff1a;栈区 ---…
阅读更多...
2.6 JAVA运算符

2.6 JAVA运算符

文章目录1.运算符概述2.运算符具体功能3.基本四则运算符4.取余运算符5.自增自减运算符6.比较运算符7.逻辑运算符8.三目运算符9.赋值运算符10.综合练习&#xff1a;求平年闰年1.运算符概述 运算符用于连接表达式的操作数&#xff0c;并对操作数执行运算。 例如&#xff0c;表达…
阅读更多...
使用java来创建es索引（基于es7.8）

使用java来创建es索引（基于es7.8）

1、先引入pom依赖&#xff1a; <dependencies> <dependency> <groupId>org.elasticsearch</groupId> <artifactId>elasticsearch</artifactId> <version>7.8.0</version> …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023