文章目录
- 📚进位计数制
- 🐇任意进制转十进制
- 🐇十进制整数转换为n进制整数
- 🐇十进制小数转换为n进制小数
- 🐇二/八/十六进制的互换
- 📚带符号的二进制数表示⭐️
- 🐇原码表示法
- 🐇补码表示法
- 🐇反码表示法
- 📚数的定点表示和浮点表示
- 🐇定点表示
- 🐇浮点表示
- 🥕浮点数的表示形式
- 🥕浮点数的表示范围
- 🥕浮点数的规格化⭐️
- 📚定点运算⭐️
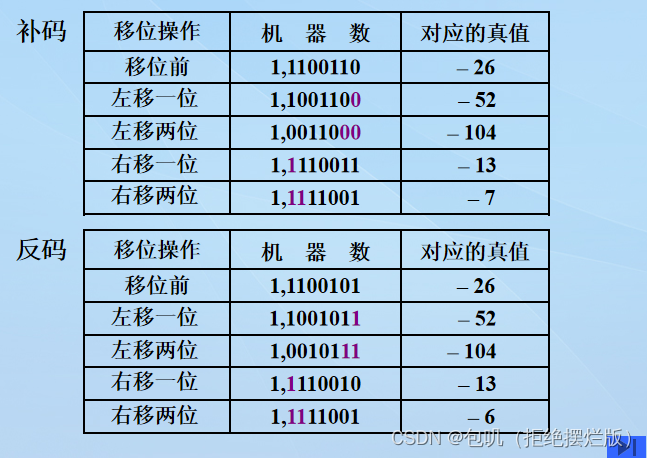
- 🐇移位运算
- 🐇补码加减运算
- 🐇定点原码一位乘法运算
- 🐇定点补码一位乘法运算
- 🐇定点原码一位除法运算
- 🥕原码恢复余数算法
- 🥕加减交替法
- 📚浮点数运算⭐️
- 🐇规格化数的判断
- 🐇浮点数运算
- 🥕浮点加减运算
- 🥕浮点乘除运算
- 📚小结
- 🔑本章掌握要点
📚进位计数制
三要素:
- 数码:每个数位上允许的数的集合
- 基数:进制中允许每个数位上选用基本数码的个数
- 位权:数码“1”在不同数位上代表的数值
🐇任意进制转十进制
按权相加法——将各位数码与权值相乘,再将各位的乘积值相加
🐇十进制整数转换为n进制整数
除n取余法(倒序)

🐇十进制小数转换为n进制小数
乘n取整法(正序)

🐇二/八/十六进制的互换
分组,按位对应转换法
-
二进制数100010转换为八进制:将每3个二进制数分为一组(从左至右),不够时补0>

-
二进制数100111010转换为十六进制:将每4个二进制数分为一组(从左至右),不够时补0

- 八进制、十六进制互相转换——
以二进制为中介
📚带符号的二进制数表示⭐️
两个基本概念
- 机器数:在计算机内部使用的,连同数符一起数码化了的数,称为机器数。
- 真值:机器数所代表的数的实际值,称为真值。
🐇原码表示法
定点整数形式
定点小数形式
🥕方法技巧
-
机器存储一个数时,“+"号编码为0,”-“号编码为1
-
数值部分:将一个数的绝对值转换为二进制
结论:
原码为符号位+数的绝对值,0正1负
🥕应用示例
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kmLdRWlt-1674621888523)(第六章:计算机的运算方法.assets/image-20230125113415677.png)]](https://img-blog.csdnimg.cn/0fd07a065be448d7931bc406f1efada5.png)
🥕原码性质
- 0可分为+0和-0,有两个编码
- 符号和数值无关
🐇补码表示法
定点整数形式
定点小数形式
ps:补码的符号位取反就是移码
🥕方法技巧
若指明定长补码,符号位1位,数值部分要补足位数,保持大小不变
- “+"号编码为0,”-“号编码为1
- 数值部分(整数、小数均适用)
- 对于正数,编码方式同原码
- 对于负数,找到右数第一个“1“,
这个“1"的左边都取反,右边(包括它自己)不变
🥕应用示例
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nUIRmTRD-1674621888524)(第六章:计算机的运算方法.assets/image-20230125120317454.png)]](https://img-blog.csdnimg.cn/fa624fc4c3d24140acb234bf17a28764.png)
🥕补码性质
- 在补码中,0有唯一的编码
- 补码适合于加减运算
- [ X + Y ] 补 = [ X ] 补 + [ Y ] 补 [X+Y]_补=[X]_补+[Y]_补 [X+Y]补=[X]补+[Y]补
- [ X − Y ] 补 = [ X ] 补 + [ − Y ] 补 [X-Y]_补=[X]_补+[-Y]_补 [X−Y]补=[X]补+[−Y]补
- 由
X
补
X_补
X补求
[
−
X
]
补
[-X]_补
[−X]补
- 对X的补码(连同符号位)求补得到
🐇反码表示法
🥕方法技巧
- 正数的反码符号位为0,数值部分就是真值
- 负数的反码符号位为1,数值部分由真值的数值部分按位取反(定长补足位数)
🥕应用示例

0的反码表示不唯一
⭕️小结
📚数的定点表示和浮点表示
小数点按约定方式标出
🐇定点表示
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1KHokIX3-1674621888527)(第六章:计算机的运算方法.assets/image-20230125123324058.png)]](https://img-blog.csdnimg.cn/705912ad540c400ba426b901ebbd49b0.png)
补码比原码反码多表示一个数(多了一个下界)
🐇浮点表示

🥕浮点数的表示形式

🥕浮点数的表示范围

- 练习:设机器数字长为 24 位,欲表示±3万的十进制数,试问在保证数的最大精度的前提下,除阶符、数符各取1 位外,阶码、尾数各取几位?

🥕浮点数的规格化⭐️
👉规格化规则
- 基数为2,尾数最高位为1
- 尾数应为纯小数,尾数的值不为0时,其绝对值应大于等于十进制的0.5而小于1
- 规格化过程(r=2)
- 左规:尾数左移1位,阶码减1
- 右规:尾数右移1位,阶码加1

补充例题——定点机和浮点机对比
📚定点运算⭐️
🐇移位运算
有符号数的移位称为算术移位
无符号数的移位称为逻辑移位
🥕算术移位规则(针对有符号数)

一道例题(关键就是规则对应)
🥕逻辑移位规则(针对无符号数)
- 逻辑左移:低位添0,高位移丢
- 逻辑右移:高位添0,低位移丢
🐇补码加减运算
🥕公式:

🥕溢出判断&&综合例题

🐇定点原码一位乘法运算
- 时序控制乘法器:加法及移位,分多步进行
- 阵列乘法器:专门逻辑电路
🥕 时序控制乘法器存在问题及解决方案
- 符号问题❓
- 定点原码乘法,符号位单独处理
- 定点补码乘法,符号位可参与运算
- 多项部分积相加的处理❓
- 将n位乘法转换为n次累加和n次移位
- 乘积的位数扩大一倍问题❓
- 通过将不再累加的低位右移,加法器的位数无需补充
🥕原码一位乘运算的基本原则
定点整数和定点小数的原码一位乘法运算相同
- 符号位单独处理
- 数值:两位数绝对值相乘
- 若数据位为n,进行n步
- 每一步:相加+逻辑右移
- 针对相加:由乘数的末位决定被乘数是否与原部分积相加(若为0则加0)
- 上例子(对照原则细看)

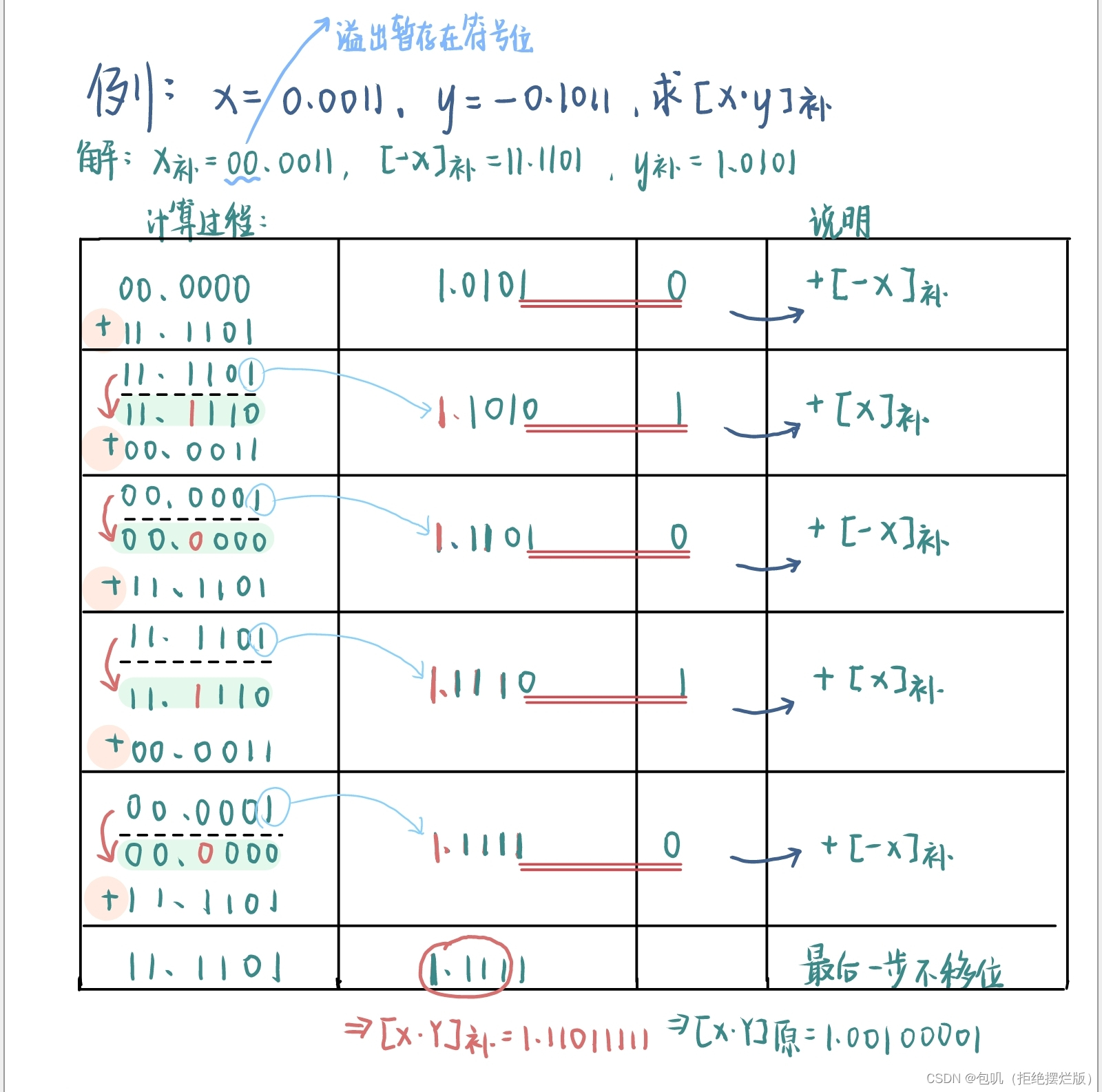
🐇定点补码一位乘法运算
🥕理论上的方法:

校正法

Booth算法


🥕实操运算原则- 符号位和数值位一同参加运算
- 若数据位为n,进行n+1次加法,n次移位
- 每步的基本操作:相加+算术右移(区别于原码一位乘的逻辑右移)

- 由乘数相邻两位的值决定相应操作,规则为:

- 上例子(对照原则细看)
| 原码乘法 | 补码乘法 | |
|---|---|---|
| 符号位 | 运算结构的符号位需单独处理 | 运算结果的符号位符号位和数值位一同参加运算 |
| 判断位 | 乘数寄存器末位1位作判断位 | 乘数寄存器最末2位作判断位 |
| 加法和移位操作 | 乘数的数据位为n,原码乘法须做n次加法,n次移位 | 乘数的数据位为n,补码乘法须做n+1次加法,n次移位 |
🐇定点原码一位除法运算

🥕原码恢复余数算法
算法规则
- Step1:首次计算余数:
被除数绝对值 - 除数绝对值( [ X ∗ ] 补 + [ − Y ∗ ] 补 [X^*]_补+[-Y^*]_补 [X∗]补+[−Y∗]补) - Step2:利用余数判断上商
- 余数为正,上商为1;
- 余数为负,上商为0,加除数的绝对值恢复原余数,即 + [ Y ∗ ] 补 +[Y^*]_补 +[Y∗]补
- 假如数据位为n,则共需进行n+1次上商判断,n次移位
- Step3:计算新余数:
[2×余数](逻辑左移)- 除数绝对值,转至Step2 - 若最后一步所得余数为负,还需恢复余数
上例子

🥕加减交替法
算法规则
- Step1:首次计算余数:
被除数绝对值 - 除数绝对值( [ X ∗ ] 补 + [ − Y ∗ ] 补 [X^*]_补+[-Y^*]_补 [X∗]补+[−Y∗]补) - Step2:根据余数
r
i
r_i
ri的符号判断上商
- 若 r i > 0 r_i>0 ri>0,上商 Q i Q_i Qi为1,计算新余数: 2 r i − y ∗ 2r_i-y^* 2ri−y∗
- 若 r i < 0 r_i<0 ri<0,上商 Q i Q_i Qi为0,计算新余数: 2 r i + y ∗ 2r_i+y^* 2ri+y∗
- 2 r i 2r_i 2ri即逻辑左移
- Step3:根据新余数再上商,假如数据位为n,则共需进行n+1次上商判断,n次移位
- 若最后一步所得余数为负,还需恢复余数
上例子

📚浮点数运算⭐️
数的浮点表示详见上文
🐇规格化数的判断
- 尾数为原码,不论正数、负数,第一数位为1
- 尾数为补码,符号位与第一数位不同
- 该判断法则有特例
- S = -1/2 = -0.1000…000
- [ S ] 补 = 1.1000...000 [S]_补=1.1000...000 [S]补=1.1000...000,非规格化形式,但其为规格化数
- S = -1
- [ S ] 补 = 1.0000...000 [S]_补=1.0000...000 [S]补=1.0000...000,符合规格化形式,但其并非为规格化数
- S = -1/2 = -0.1000…000
🐇浮点数运算
🥕浮点加减运算
- Step1: 对阶

- Step2:尾数补码加减
- Step3:规格化
- 规格化判断
- 左规:
尾数左移一位,阶码减1,直到数符和第一数位不同为止 - 右规:
当尾数溢出(>1)时,需右规
上例子

🥕浮点乘除运算

📚小结
🔑本章掌握要点
- 掌握原反补码转换
- 掌握真值与浮点机器数的相互转换
- 定点数的补码加减运算,以及溢出判断
- 定点数的乘法(原码一位、补码一位)运算
- 除法加减交替运算
- 浮点数规格化
- 掌握浮点数的补码加减运算
- 了解浮点数的乘除运算步骤
👀参考博客
进制的概念与转换(二进制、十进制、八进制、十六进制)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3EwyHWut-1674621888522)(第六章:计算机的运算方法.assets/image-20230125113054736.png)]](https://img-blog.csdnimg.cn/db70b4fb07ce472bbaf8df05494b48b3.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FzRFKkFL-1674621888522)(第六章:计算机的运算方法.assets/image-20230125113139011.png)]](https://img-blog.csdnimg.cn/238703f9d21f4247afed3526073e0411.png)

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nx719C0Z-1674621888523)(第六章:计算机的运算方法.assets/image-20230125113706891.png)]](https://img-blog.csdnimg.cn/faf9cab8f76d430d876cc088621722f7.png)