AI短片制作全流程详解——掌握未来视频创作新技能！

news2025/1/16 1:39:15

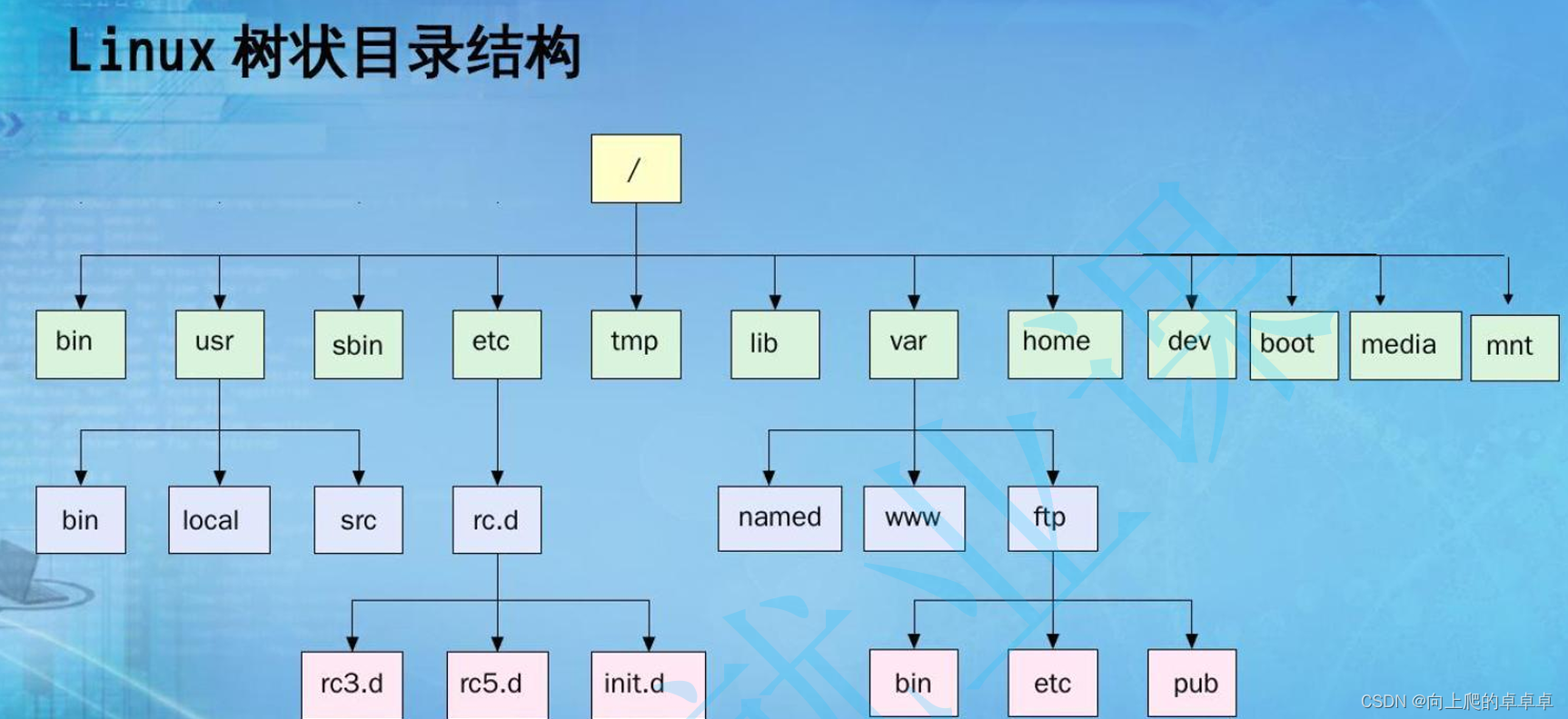
老铁们! 期待已久的AI短片免费直播分享来了！！！

还是老规矩，只讲干货，全程不废话!

在这个直播中，我们将深入探讨AI短片制作的全过程，从构思到最终输出，全方位解析每一个步骤的关键要素和难点。无论你是视频制作的新手，还是希望提升技能的专业人士，这次直播都将为你带来满满的干货和实用技巧！

alt

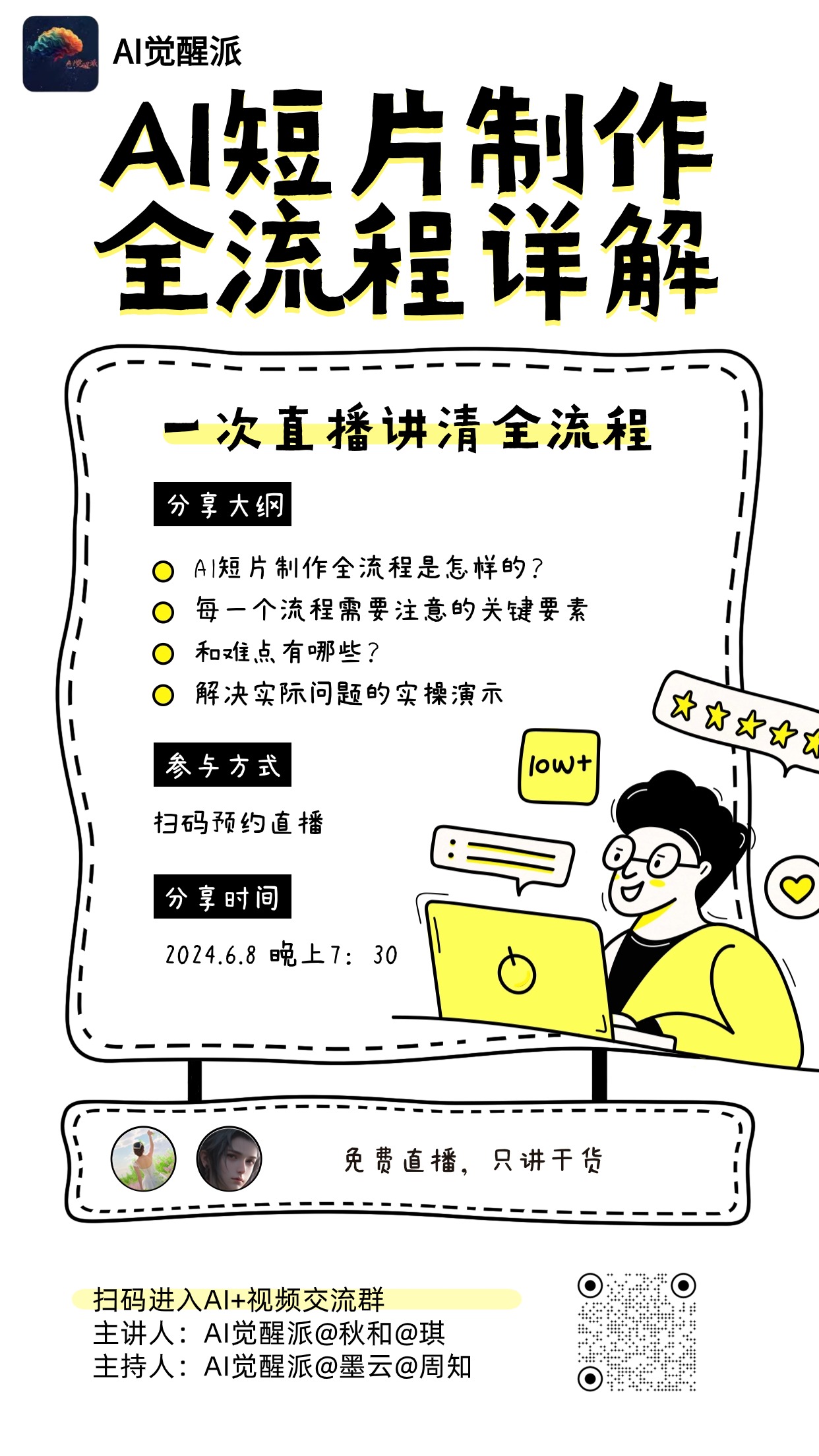
无论你是在寻找灵感，还是想要提升制作技巧，这次直播都将成为你短片制作之旅的重要指南。让我们一起探索AI技术带来的无限可能，创造出独具特色的精彩短片！

直播时间：

2024.06.08 晚 7:30

直播平台：

小鹅通, 扫码入群后，群公告获取直播地址!

期待与你在直播间见面！

本文由 mdnice 多平台发布

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1791071.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Ant Design Vue Table组件全单元格编辑实现方案

Ant Design Vue Table组件全单元格编辑实现方案

在ant上的table常见用法是一行的元素可编辑&#xff0c;如下&#xff1a; 但是现在有一个需求是全部单元格均可编辑&#xff0c;如何实现呢&#xff1f; 表格组件 <a-tablev-if"query.personnel_type 0"size"middle"row-key"id":scroll&qu…
阅读更多...
中继器、集线器、网桥、交换机、路由器和网关

中继器、集线器、网桥、交换机、路由器和网关

目录 前言一、中继器、集线器1.1 中继器1.2 集线器 二、网桥、交换机2.1 网桥2.1.1 认识网桥2.1.2 网桥的工作原理2.1.3 生成树网桥 2.2 交换机2.2.1 交换机的特征2.2.2 交换机的交换模式2.2.3 交换机的功能 三、路由器、网关3.1 路由器的介绍3.2 路由器的工作过程3.2.1 前置知…
阅读更多...
迅雷极简易下载

迅雷极简易下载

一、简介 1、迅雷是一家全球领先的去中心化服务商&#xff0c;以技术构建商业&#xff0c;以服务创造共识&#xff0c;从而建立一个高效可信的存储与传输网络。 迅雷成立于2003年&#xff0c;总部位于中国深圳&#xff0c;2014年于纳斯达克上市&#xff08;纳斯达克股票代码&a…
阅读更多...
Threejs墙体挖洞做门或窗

Threejs墙体挖洞做门或窗

在使用Threejs代码构建的展厅中&#xff0c;需要在一面墙中间挖个洞作为门或窗户&#xff0c;效果如下&#xff1a; 引入ThreeBSP.js <script src"plugins/three/ThreeBSP.js"></script> 创建 // 1 定义墙面var cubeGeometry new THREE.BoxGeometry(1…
阅读更多...
4.2 索引及其操作

4.2 索引及其操作

对数据库中的表进行查询操作时有两种搜索扫描方式&#xff0c;一种是全表扫描&#xff0c;另一种就是使用表上建立的索引进行扫描。 全表扫描要查找某个特定的行&#xff0c;必须从头开始一一查看表中的每一行&#xff0c;与查询条件做对比&#xff0c;返回满足条件的记录&…
阅读更多...
FFA-Net：用于单图像去雾的特征融合注意力网络

FFA-Net：用于单图像去雾的特征融合注意力网络

摘要 论文链接&#xff1a;https://arxiv.org/pdf/1911.07559v2 在这篇论文中&#xff0c;我们提出了一种端到端的特征融合注意力网络&#xff08;FFA-Net&#xff09;来直接恢复无雾图像。FFA-Net架构由三个关键组件组成&#xff1a; 一种新颖的特征注意力&#xff08;FA&…
阅读更多...
Mac下删除系统自带输入法ABC，正解！

Mac下删除系统自带输入法ABC，正解！

一、背景说明 MacOS 在 14.2 以下的系统存在中文输入法 BUG&#xff0c;会造成系统卡顿&#xff0c;出现彩虹圆圈。如果为了解决这个问题&#xff0c;有两种方法&#xff1a; 升级到最新的 14.5 系统使用第三方输入法 在使用第三方输入法的时候&#xff0c;会发现系统自带的 …
阅读更多...
[论文笔记]Mixtral of Experts

[论文笔记]Mixtral of Experts

引言 今天带来大名鼎鼎的Mixtral of Experts的论文笔记&#xff0c;即Mixtral-8x7B。 作者提出了Mixtral 8x7B&#xff0c;一种稀疏专家混合(Sparse Mixture of Experts&#xff0c;SMoE)语言模型。Mixtral与Mistral 7B具有相同的架构&#xff0c;不同之处在于每个层由8个前馈…
阅读更多...
数据结构【树】（理论篇）

数据结构【树】（理论篇）

树的概念 树是一个非线性的数据结构&#xff0c;前面我们学习的顺序表、链表等等等等&#xff0c;他们的逻辑结构都是成一条线的&#xff0c;都是所有元素都是排成一条的&#xff1b;而树他是有多个分支的&#xff0c;是发散的。 树是由n&#xff08;n>0&#xff09;个有限…
阅读更多...
AI编程新手快速体验SpringCloud Alibaba 集成AI功能

AI编程新手快速体验SpringCloud Alibaba 集成AI功能

上周六写了一篇文章 震撼发布&#xff01;Spring AI 框架重磅上线&#xff0c;Java 集成 AI 轻松搞定&#xff01; 部分同学可能没有科学上网的条件&#xff0c;本地ollama 集成又比较笨重。趁着周六&#xff0c;写一篇基于SpringCloud Alibaba 集成AI的文章。 先简单介绍…
阅读更多...
Ollama教程，本地部署大模型Ollama，docker安装方法，仅供学习使用

Ollama教程，本地部署大模型Ollama，docker安装方法，仅供学习使用

不可商用&#xff01;&#xff01;仅仅提供学习使用&#xff01; 先上视频教学&#xff1a; Ollama教程&#xff0c;本地部署大模型Ollama&#xff0c;docker安装方法&#xff0c;仅供学习使用&#xff01; 资料获取 &#xff1a; Ollama下载包和安装文档在这里&#xff…
阅读更多...
AI大模型还没有到卷长文的时候

AI大模型还没有到卷长文的时候

AI风口上&#xff0c;国内大模型技术突飞猛进&#xff0c;很多人都沉浸在用AI来辅助办公&#xff0c;辅助学习等等工具化应用落地&#xff0c;但也有趁着风口想大赚一笔&#xff0c;为了估值什么都敢说的。 前几天&#xff0c;Kimi对外宣称自己的技术狂飙到能读200万字甚至100…
阅读更多...
webgl_decals

webgl_decals

ThreeJS 官方案例学习&#xff08;webgl_decals&#xff09; 1.效果图 2.源码 <template><div><div id"container"></div></div> </template> <script> // 光线投射相关代码 https://threejs.org/docs/index.html#api/z…
阅读更多...
一文了解JVM面试篇（上）

一文了解JVM面试篇（上）

Java内存区域 1、如何解释 Java 堆空间及 GC？ 当通过 Java 命令启动 Java 进程的时候，会为它分配内存。内存的一部分用于创建 堆空间，当程序中创建对象的时候，就从对空间中分配内存。GC 是 JVM 内部的一 个进程，回收无效对象的内存用于将来的分配。 2、JVM 的主要组成…
阅读更多...
天润融通，荣获2024中国AI应用层创新企业

天润融通，荣获2024中国AI应用层创新企业

AI技术发展日新月异&#xff0c;可谓“AI一天&#xff0c;人间一年”。 从2023年到2024年&#xff0c;短短一年的时间&#xff0c;大模型技术的发展就已经逐步从追求“技术突破”转向了追求“应用落地”。如何将大模型的技术与企业的生产、运营、销售等场景结合起来&#xff0…
阅读更多...
Vue——子级向父级传递数据(自定义事件)

Vue——子级向父级传递数据(自定义事件)

文章目录 前言子级向父级传递数据实现浏览器效果展示 前言 在上一篇博客中&#xff0c;说到了父级向子级组件中传递对应的数据信息&#xff0c;以及增加传递数据的类型现在、默认值填充等规则。 Vue——组件数据传递与props校验 但使用props只能是单向的数据传递&#xff0c;也…
阅读更多...
门外汉一次过软考中级（系统集成项目管理工程师）秘笈，请收藏！

门外汉一次过软考中级（系统集成项目管理工程师）秘笈，请收藏！

24上软考考试已经结束&#xff0c;24下软考备考又要开启了&#xff01;今年软考发生了改革&#xff0c;很多考试由一年考两次变成了一年考一次&#xff0c;比如高级信息系统项目管理师&#xff0c;比如中级系统集成项目管理工程师&#xff0c;这两科是高、中级里相对简单&#…
阅读更多...
vue2的element的table组件使用form校验

vue2的element的table组件使用form校验

1.需求描述 vue2有时候做自增表格el-table&#xff0c;希望能够带一些校验&#xff0c;但又不想手搓校验逻辑&#xff0c;可以借用el-form的校验逻辑。 2.代码处理 1. html <template><div class"sad-cont"><el-form ref"form" :model&…
阅读更多...
小程序跳转1688＜web-view＞无效后的实现

小程序跳转1688＜web-view＞无效后的实现

web-view 跳转方式 1&#xff1a;这种方法需要在微信开发平台 -> 开发管理 -> 业务域名中配置好要跳转的网站域名&#xff1b; 2&#xff1a;基本上跳转的网址是第三方就不可以配置&#xff0c;因为配置需要在这个域名中的根目录上放你的验证文件&#xff1b; <web-v…
阅读更多...
爬楼梯——动态规划第一步

爬楼梯——动态规划第一步

本问题其实常规解法可以分成多个子问题&#xff0c;爬第 n 阶楼梯的方法数量&#xff0c;等于两个部分之和 爬上 n−1 阶楼梯的方法数量。因为再爬 1 阶就能到第 n 阶爬上 n−2 阶楼梯的方法数量&#xff0c;因为再爬 2 阶就能到第 n 阶 所以我们得到公式 dp[n] dp[n−1] d…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023