动态规划——浅谈dp如何入门,以及入门题目(值得收藏,持续更新)

news2025/1/19 20:22:06

前言

动态规划如何入门?如果你问我怎么精通,那我只能告诉你我也不知道,但你要问我怎么入门,那我就可以和你说道说道了.

我并没有能力也不想说你看完就会了,我只是想给大家开个头,你只要知道怎么写了怎么去思考了,你就可以通过刷题来强化思维了,能走多远就看各位的造化了!

动态规划入门须知

动态规划（Dynamic Programming, DP）是一种通过将复杂问题分解为更小的子问题并解决这些子问题来构建解决方案的算法设计方法。动态规划的核心是状态转移方程，它定义了如何从一个或多个已知状态转换到一个新的状态。状态转移方程是动态规划问题的递推关系，用于描述当前状态与之前状态的关系。

想要做好一道动态规划题,或者说想要写所有的动态规划题,基本上都是按照这个步子走

1.设计状态表示

dp,其实也是记忆化存储,不过dp数组存的是题目需要你求的最优解(后续看题目来说)

在开始写代码之前,我们基本上要提前想要dp数组是一维的,二维的,还是三维的,然后呢,数组的值代表什么,这个真的很重要!!!!,基本上dp 数组的值,就是我们的答案

2.状态转移方程

什么叫状态转移方程呢,说实话,笔者也很为难,自己都是半桶水,还想教会别人.

通俗地说，状态转移方程就是一个规则或公式，告诉你如何从已知的信息（以前的结果）推导出未知的信息（当前的结果）。就像搭积木一样，你用之前已经搭好的积木，按照一定的规则，搭建出新的积木。

3.确定初始条件以及边界

在状态转移方程开始之前,总要有开始的值吧,而且有时候还会有一些边界值要你人为设置的.

4.代码实现

所有东西都构思好了,就要代码实现了

你说上面都是写的什么玩意,我看不懂?没关系,看不懂就对了,因为我一开始也是蒙的,接下来

看一些题目吧,看完这些题目你还不会入门,那你来骂我好了

题目一

1137. 第 N 个泰波那契数 - 力扣（LeetCode）

这题就是最简单的入门题,为什么?因为他已经告诉你状态转移方程了

Tn+3 = Tn + Tn+1 + Tn+2

那么,我们的状态表示怎么写呢?

dp[] 数组应该这么表示 dp[i] 表示,第i个位置的泰波那契数的值

然后边界也以及告诉你了,T0 = 0, T1 = 1, T2 = 1.

所以说,我们就可以开始写了

class Solution {
public:
    int tribonacci(int n) 
    {
        if(n==0) return 0;
        if(n==1||n==2) return 1;
        vector<int> dp(n+1);
        dp[0]=0,dp[1]=dp[2]=1;
       int a=0,b=1,c=1,d=0;
        for(int i=3;i<=n;i++)
        {
        //   d=a+b+c;
        //   a=b;
        //   b=c;
        //   c=d;
           dp[i]=dp[i-1]+dp[i-2]+dp[i-3];
        }
      return  dp[n];
    }
};

这个是常规写法,可以看到,每一步都是有迹可循的,按照上面的四步走写的

dp[] 数组应该这么表示 dp[i] 表示,第i个位置的泰波那契数的值

Tn+3 = Tn + Tn+1 + Tn+2 是状态转移方程

dp[0]=0,dp[1]=dp[2]=1; 是初始条件

最后实现代码

当然了,这里也有更优化的写法,就是滚动的数组

class Solution {
public:
    int tribonacci(int n) 
    {
        if(n==0) return 0;
        if(n==1||n==2) return 1;
        vector<int> dp(n+1);
        dp[0]=0,dp[1]=dp[2]=1;
       int a=0,b=1,c=1,d=0;
        for(int i=3;i<=n;i++)
        {
          d=a+b+c;
          a=b;
          b=c;
          c=d;
        }
      return  d;
    }
};

这里 a,b,c,d就好像一个滚动的桶,一直在往前走,然后最后d 就是答案.

题目二

LCR 088. 使用最小花费爬楼梯 - 力扣（LeetCode）

这题就稍微稍微有点难了

状态表示

首先,我们的状态表示最好是根据答案来的,答案要我们求最小花费.

那我们的dp数组怎么表示呢还是 dp[i],一维数组,我们可以这么看,dp[i] 表示如果你需要走到第 i 个台阶,所需要的最小花费,那么我们就可以记数组的大小为 n, 然后dp[n] 就是我们的答案

转移方程

我第 i 个的花费源于哪里?不是第 i-1 个台阶就是第 i-2个台阶吧,我们只要取这两个的最小值加起来,是不是就可以表示,这是最小花费了?

还是不太懂大伙可以看图

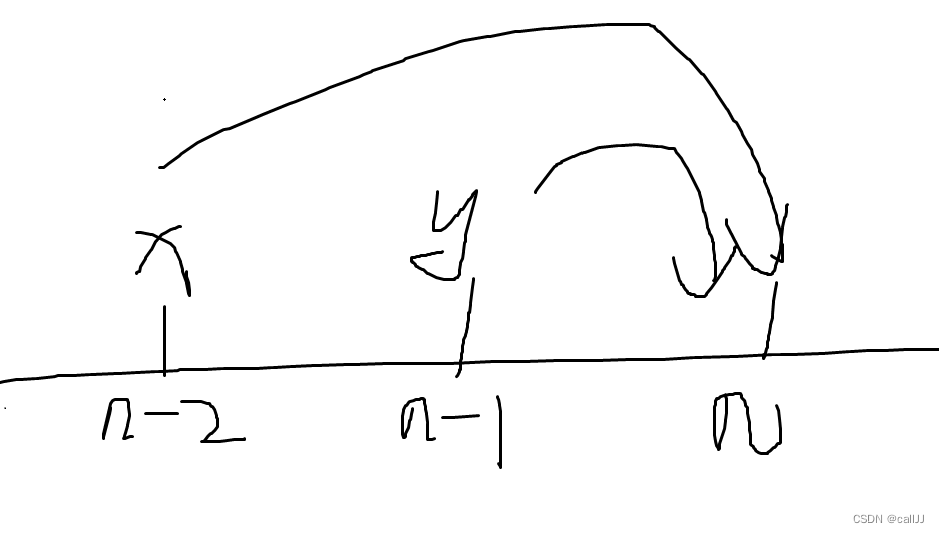
cost 数组是台阶花费数组

我是花费x 走到 n 呢,还是花费y 走到 n 呢? 那就看谁更小了,然后加上原本的花费,别忘了

dp[] 表示花费

dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])

边界设置

这题没什么需要在意的,就是正常写就可以了,一开始dp 数组都是0

需要注意的是,我们是每个台阶都会算到的,所以不用担心说什么哎呀我某个台阶会不会没算到啊

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost)
{
  int  n=cost.size();

  vector<int> dp(n+1);

  for(int i=2;i<=n;i++)
  {
    dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
  }
  return dp[n];
    }
};