本文为离散数据与组合数学电子科技大学王丽杰老师的课程笔记，详细视频参考
【电子科技大学】离散数学（上） 王丽杰
【电子科技大学】离散数学（下） 王丽杰
latex的离散数学写法参考： 离散数学与组合数学-01

离散数学公式
!符号 代码 含义
$\wedge$ \wedge 且
$\vee$ \vee 或
$\cap$ \cap 交
$\cup$ \cup 并
$\subseteq$ \subseteq 子集
$⊈$ \nsubseteq 不是子集
$\subset$ \subset 真子集
$\not\subset$ \not\subset 不是真子集
$\in$ \in 属于
$\notin$ \not\in 不属于
$\leftrightarrow$ \leftrightarrow 等价
$\iff$ \Leftrightarrow 等值
$\neg$ \neg或\lnot 非
$\mathbb{R}$ \mathbb{R} 实数集
$\mathbb{Z}$ \mathbb{Z} 整数集
$\varnothing$ \varnothing 空集
$\forall$ \forall 对任意的
$\exists$ \exists 存在
$\ge$ \geq大于等于
$\le$ \leq 小于等于

下标的输入命令是：$x_{内容}$ x_{内容}
上标的输入命令式：$x^2$ x^2
空格 \quad

$R/$ R\mkern-10.5mu/ 数值越大，斜杆越往字母左侧移动

离散数学与组合数学-04图论上

4.1 图的引入

4.1.1 图的示例

图论发源于十八世纪, 最早主要研究一些游戏问题: 如哥尼斯堡七桥问题, 迷宫问题和博弈问题等. 计算机出现以后, 图论得到了长足的发展, 至今仍然活跃在科研和实际应用的第一线, 如现在受到普遍关注的云计算, 大数据应用和深度学习等.
图论所讨论的图 (Graph) 与人们通常所熟悉的图 (如圆、椭圆、函数图表等) 是很不相同的.图论中的图是指某类具体离散事物集合和该集合中的每对事物间以某种方式相联系的数学模型.

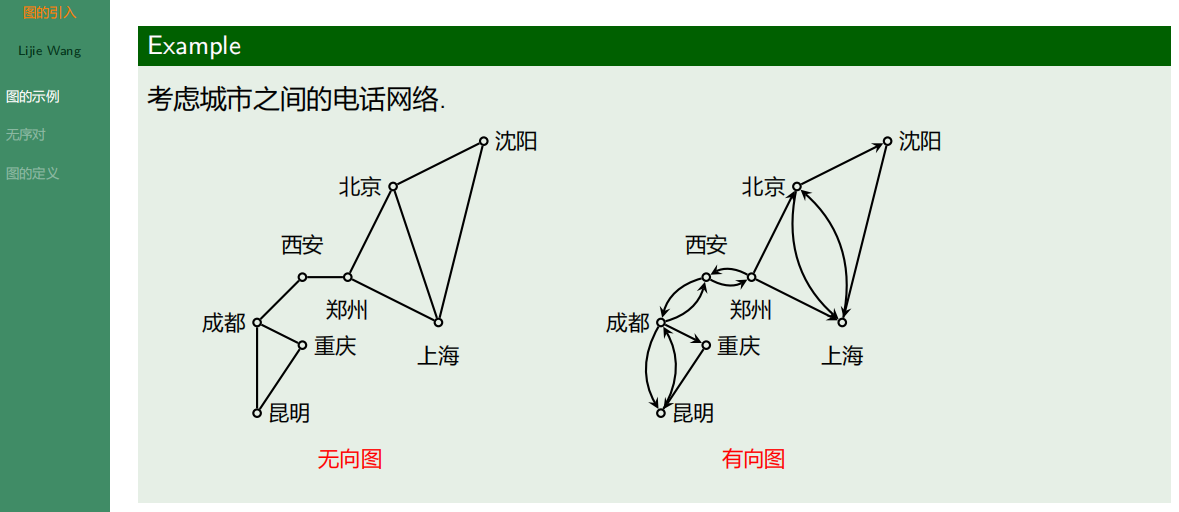
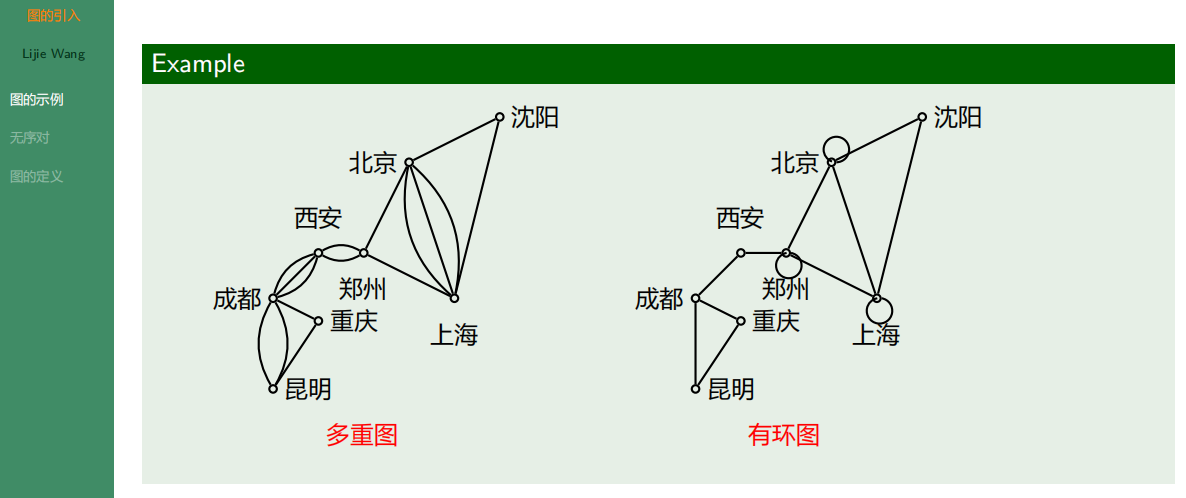
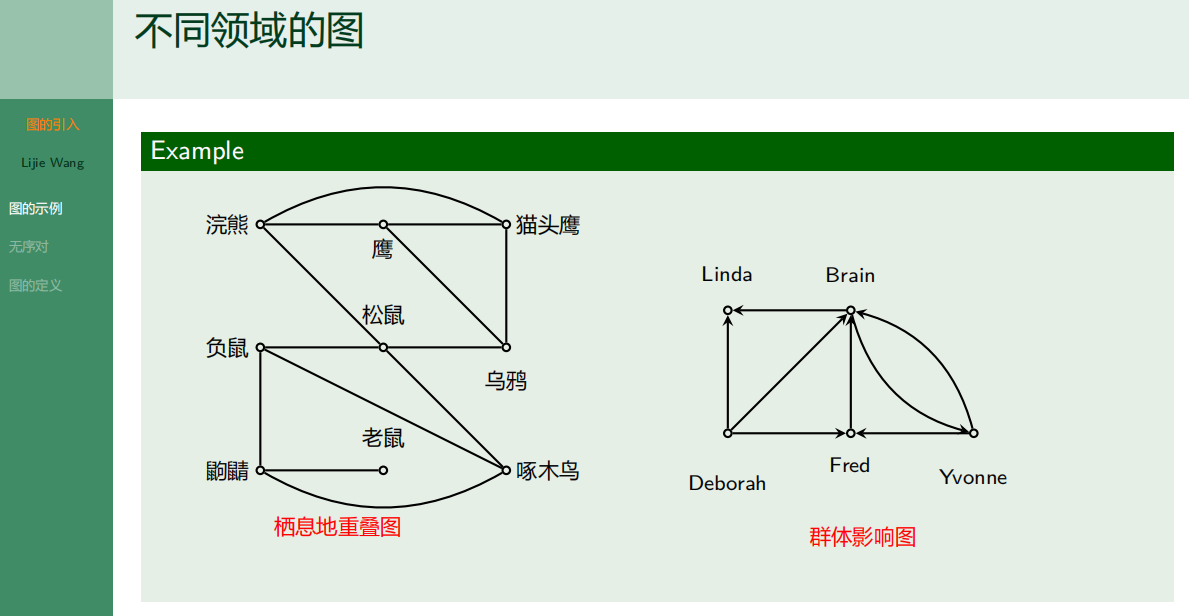
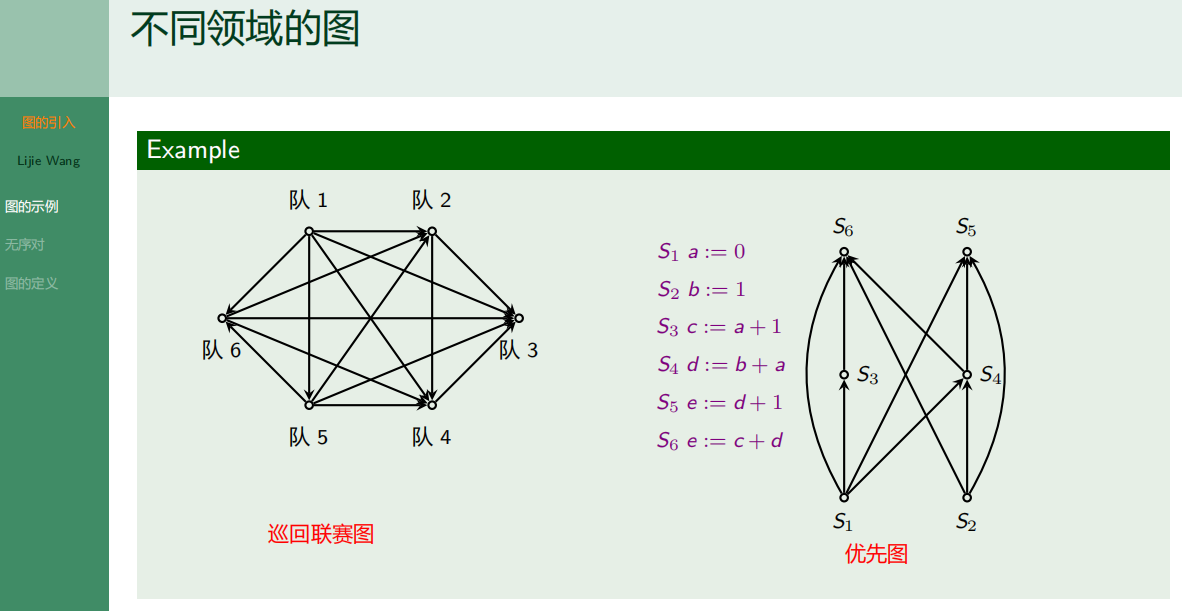
4.1.2 无序对和无序积

4.1.3 图的定义

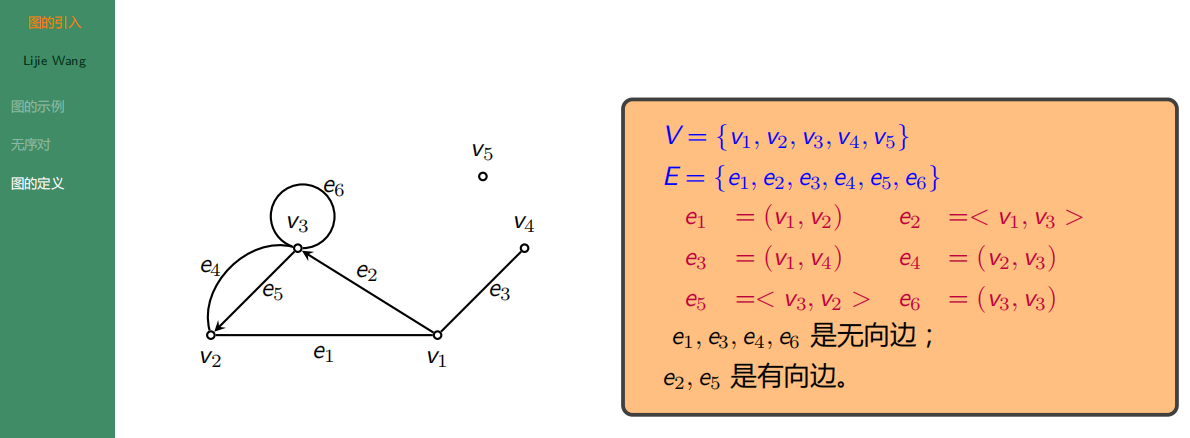
4.2 图的表示

4.2.1 集合表示和图形表示

4.2.2 矩阵表示法

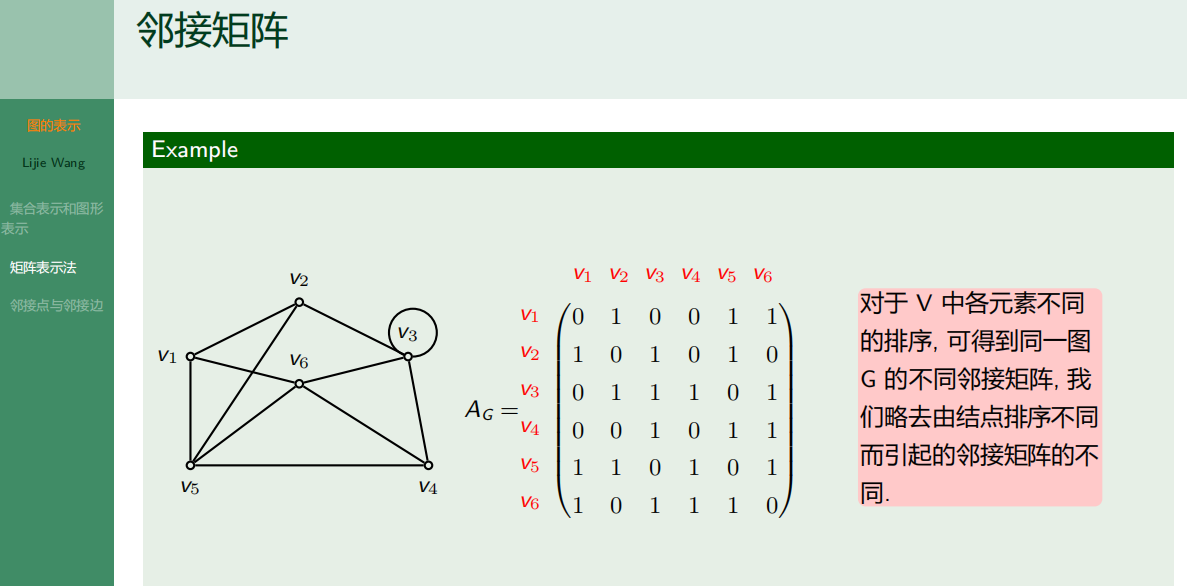
4.2.3 邻接点与邻接边

4.3 图的分类

4.3.1 按边的方向分类

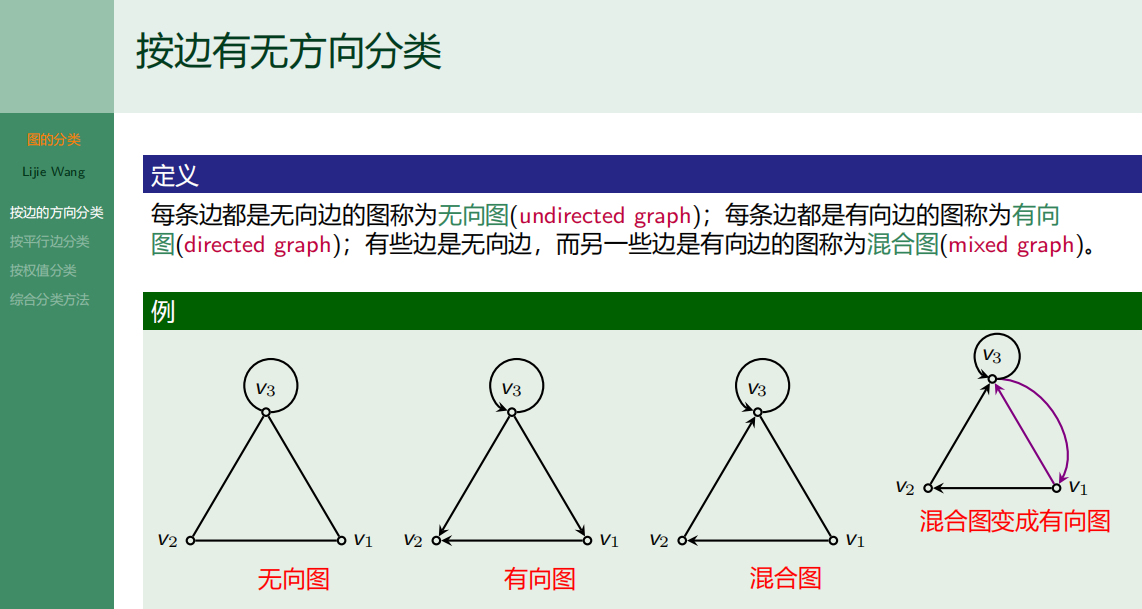
4.3.2 按平行边分类

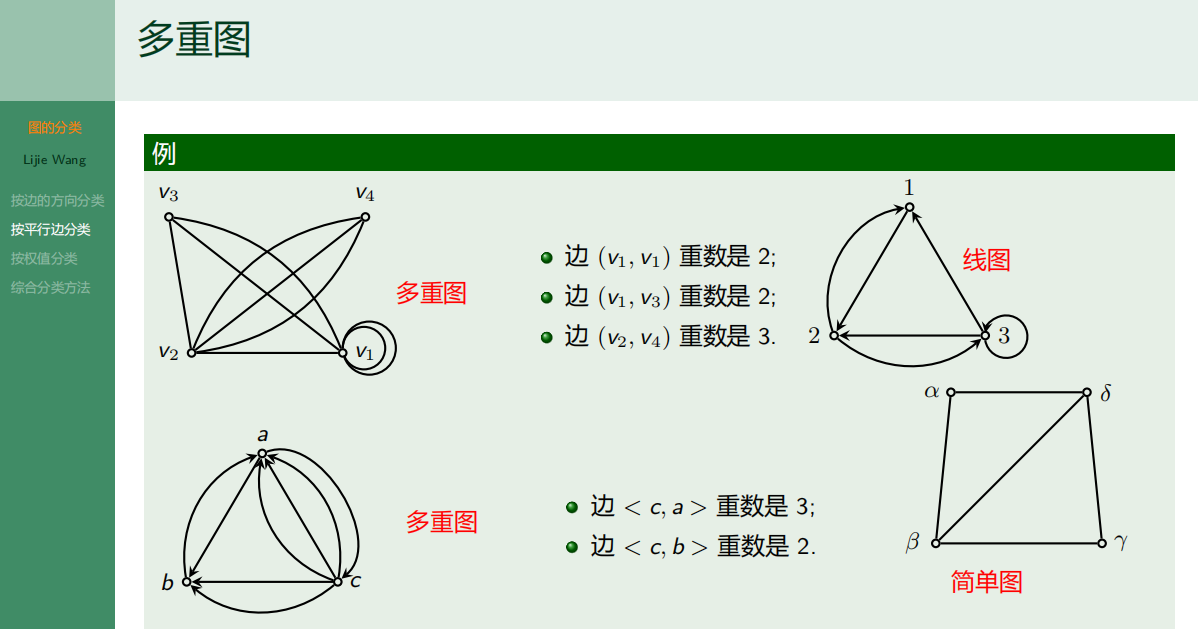
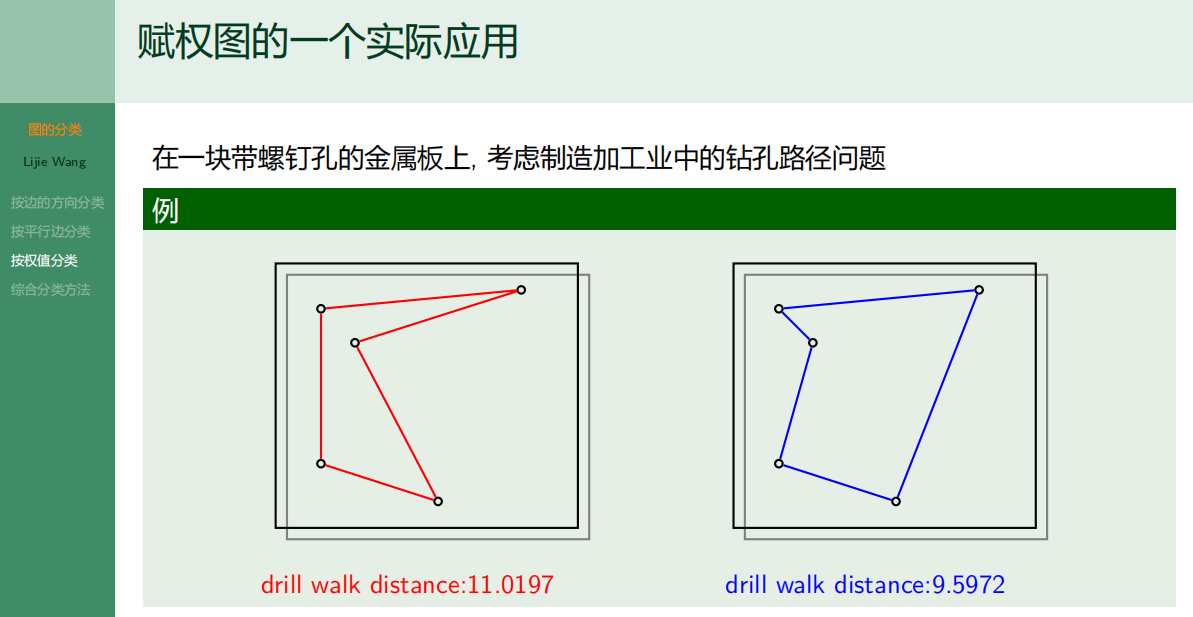
4.3.3 按权值分类

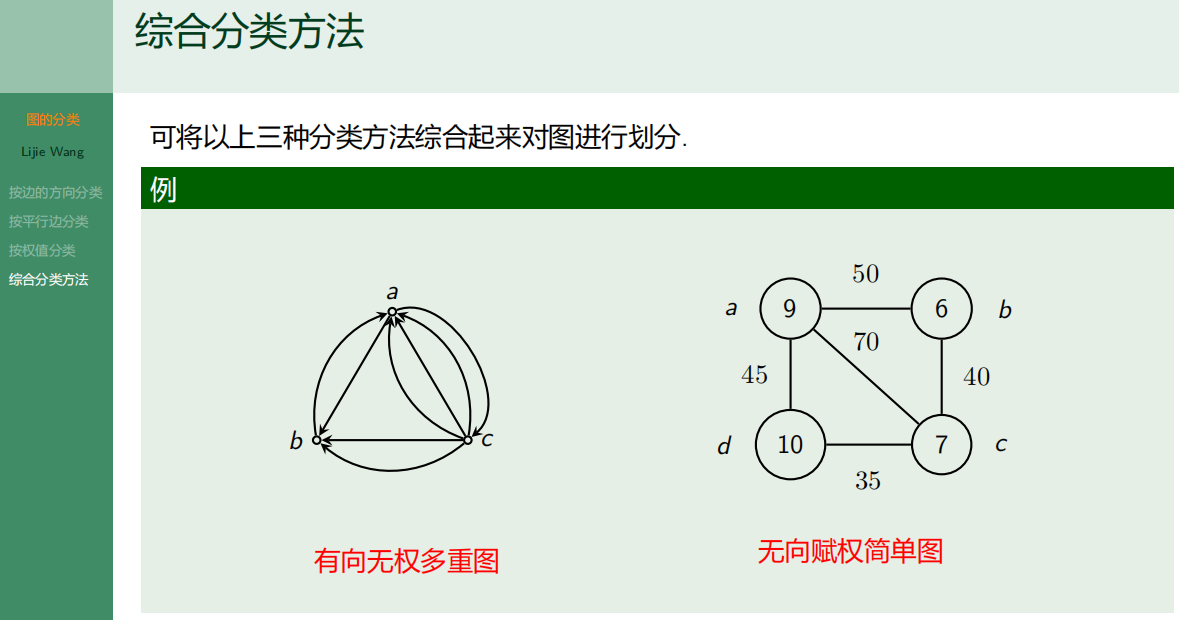
4.3.4 综合分类方法

4.4 图论基础-子图和补图

4.4.1 子图

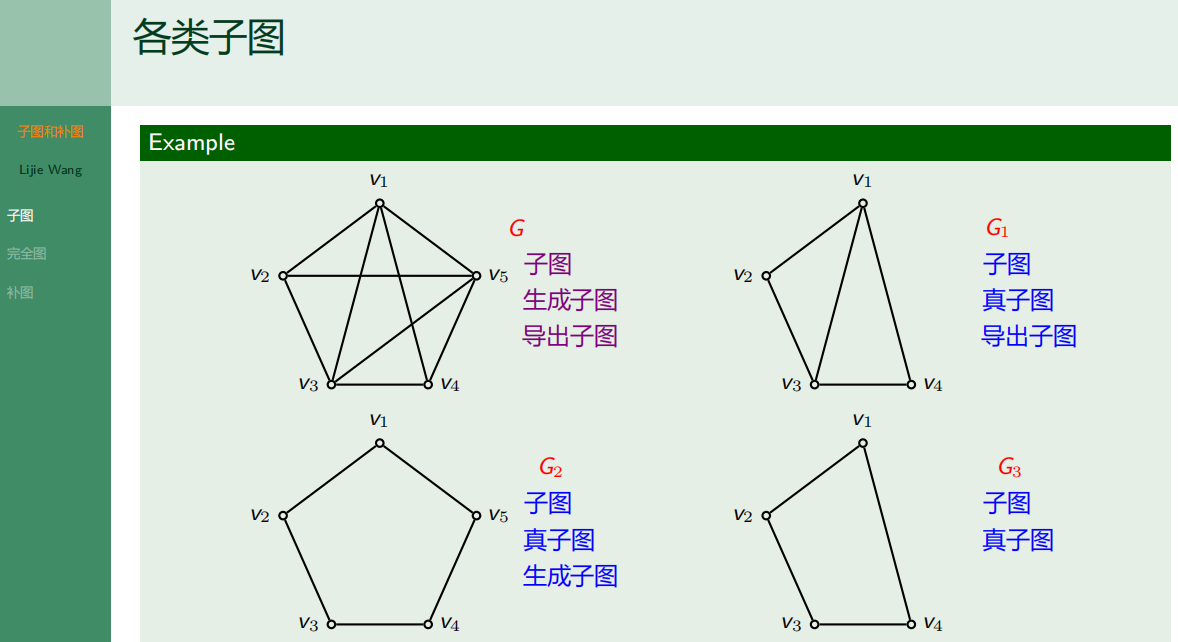
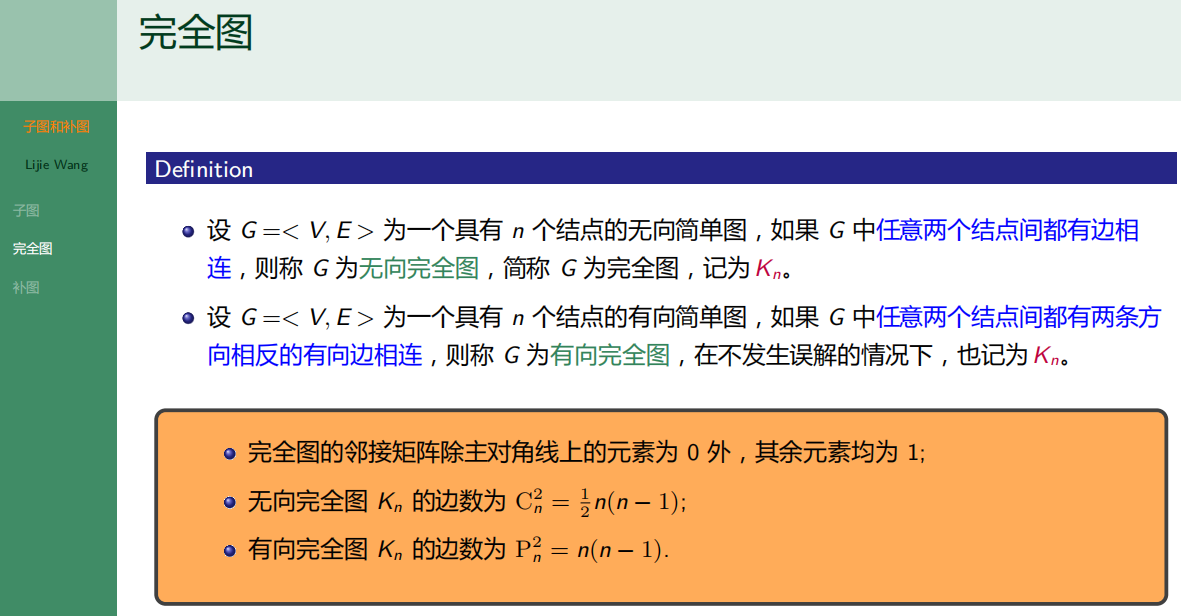
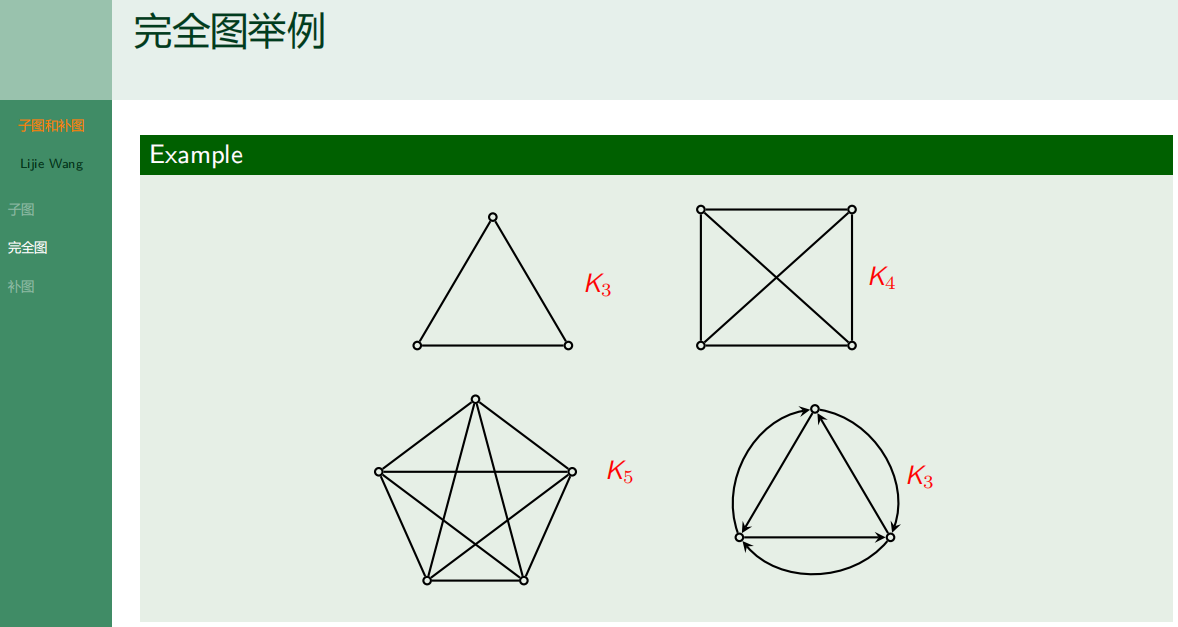
4.4.2 完全图

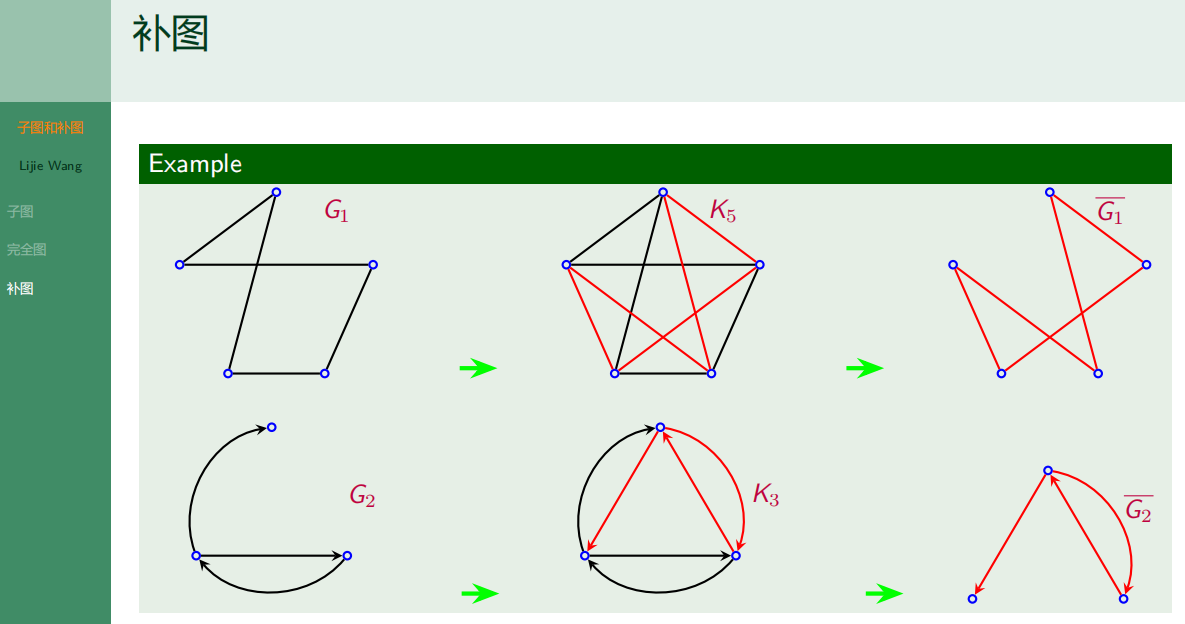
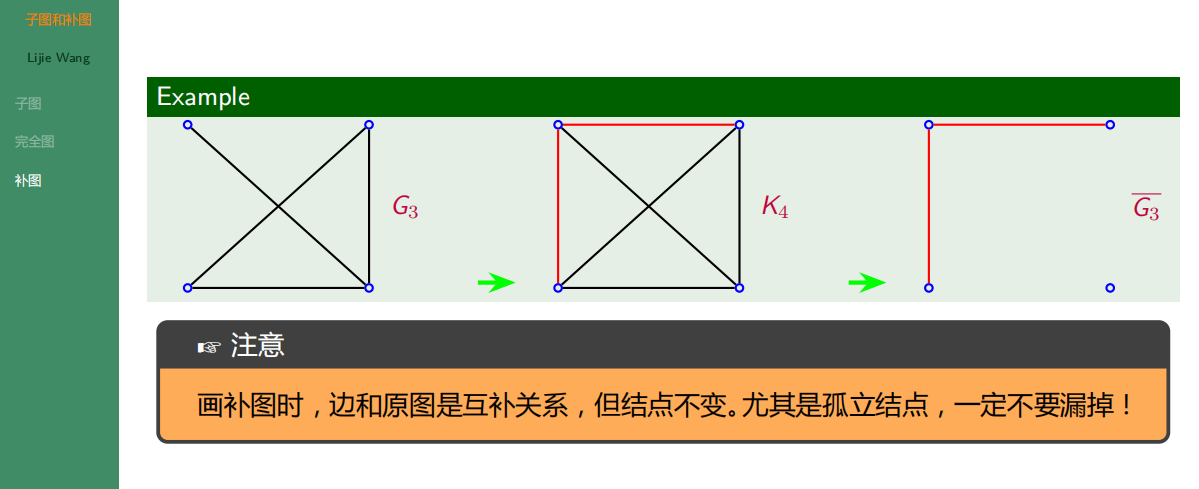
4.4.3 补图

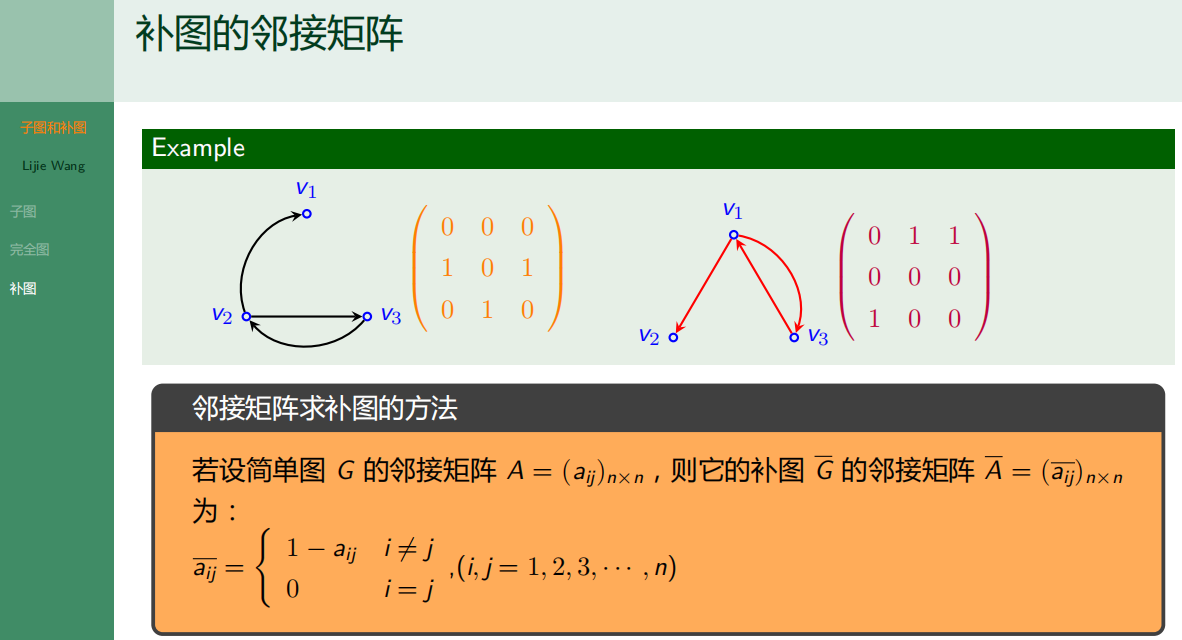
4.5 图论基础-握手定理

4.5.1 结点的度数

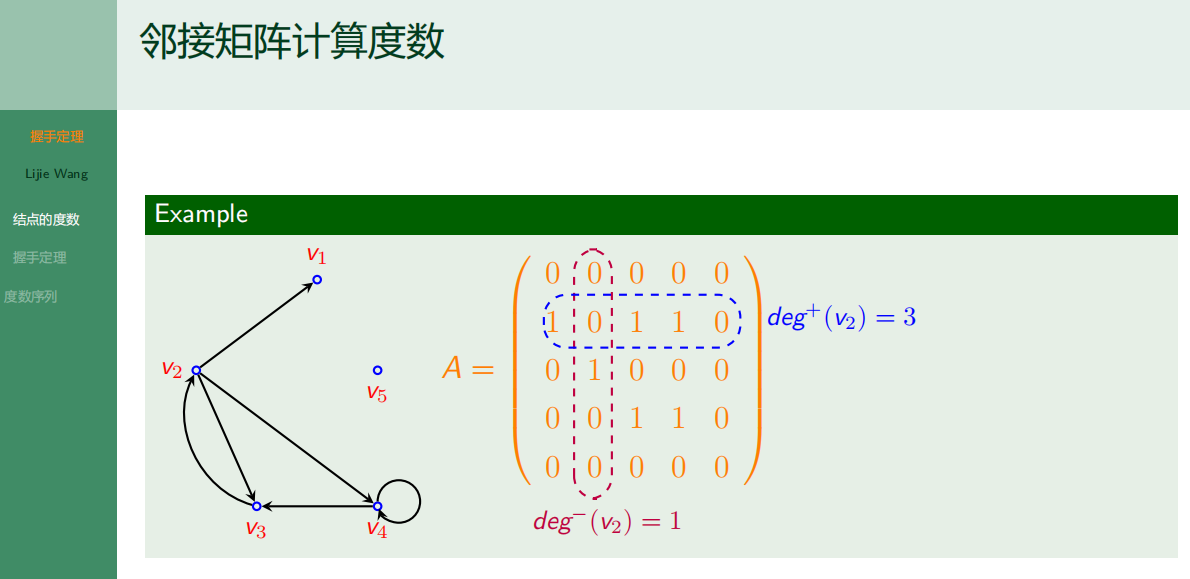
4.5.2 握手定理

4.5.3 图的度数序列

4.6 图论基础-图的重构

4.6.1 引言

4.6.2 图的同构定义

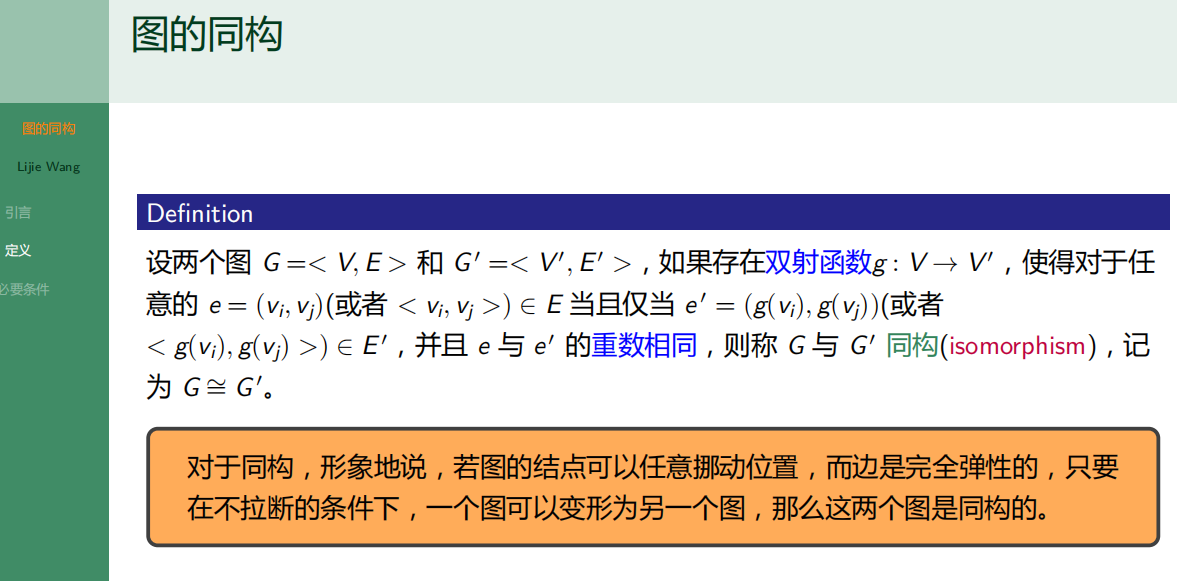
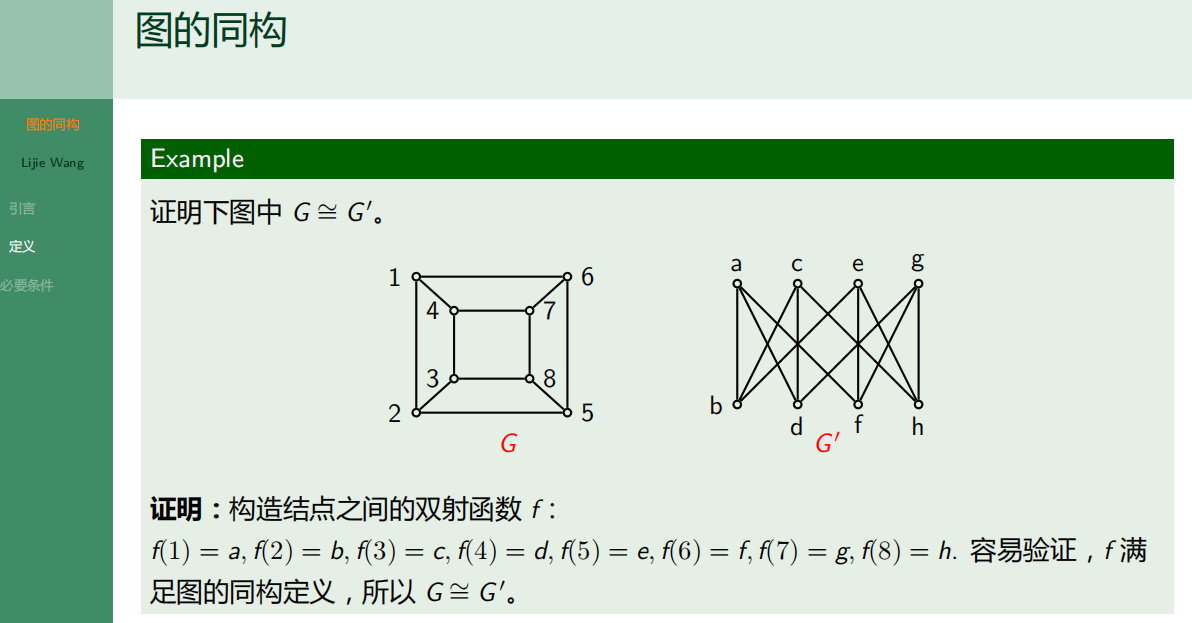
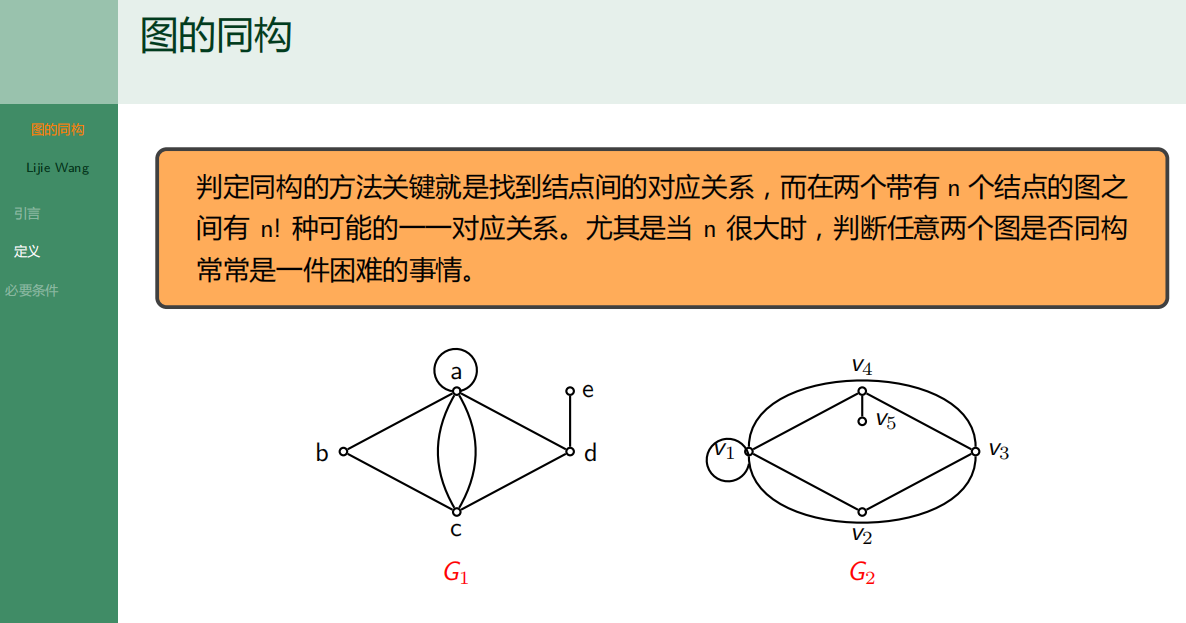
4.6.3 图同构的必要条件

4.7 图论基础-通路和回路

4.8 图论基础-可达性与最短通路

4.9 图论基础-无向图的连通性

4.10 图论基础-有向图的连通性

4.11 图论基础-认识树