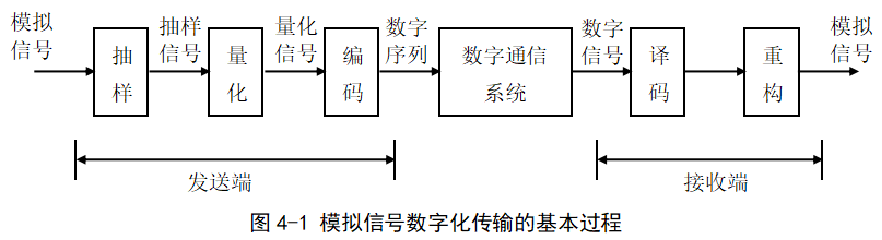
模拟信号的数字化传输
将模拟信号转换为数字信号，称为 模拟信号的数字化，一般需要经过 抽样、 量化和 编码三个步骤。
转换得到的数字信号可以直接在数字基带系统中传输，也可以将其进行调制后通过数字调制系统中传输。

1 抽样及抽样定理

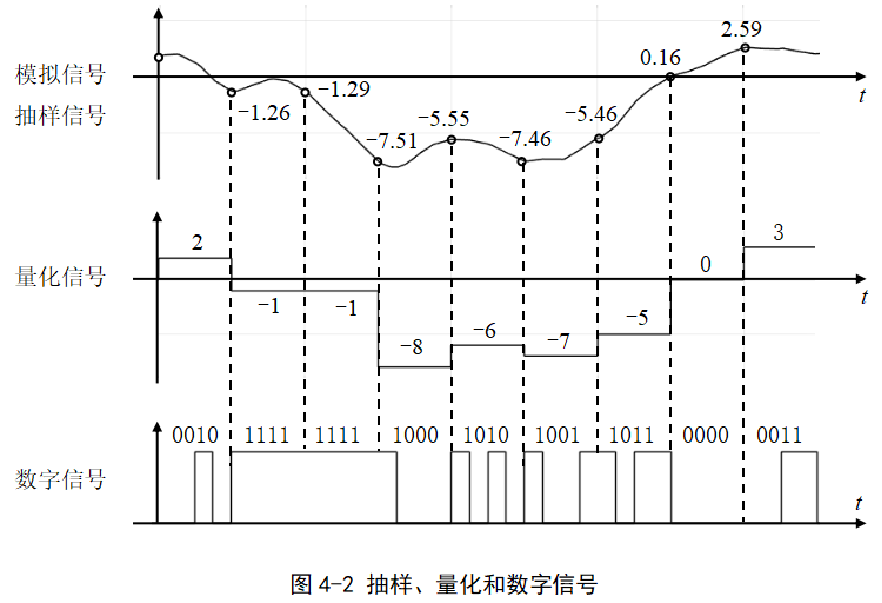
抽样（Sample） 是在发送端将模拟信号转换为离散信号的过程。
接收端通过重构将离散信号还原为模拟信号。

1.1 抽样

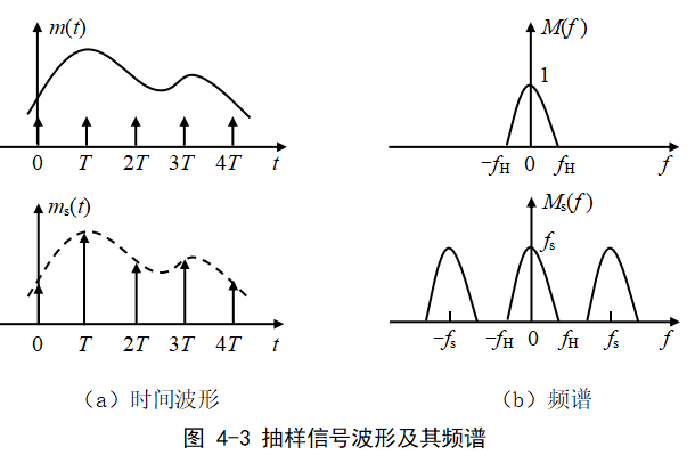
• 抽样信号为冲激序列，各时刻的抽样值随模拟信号的幅度而变化
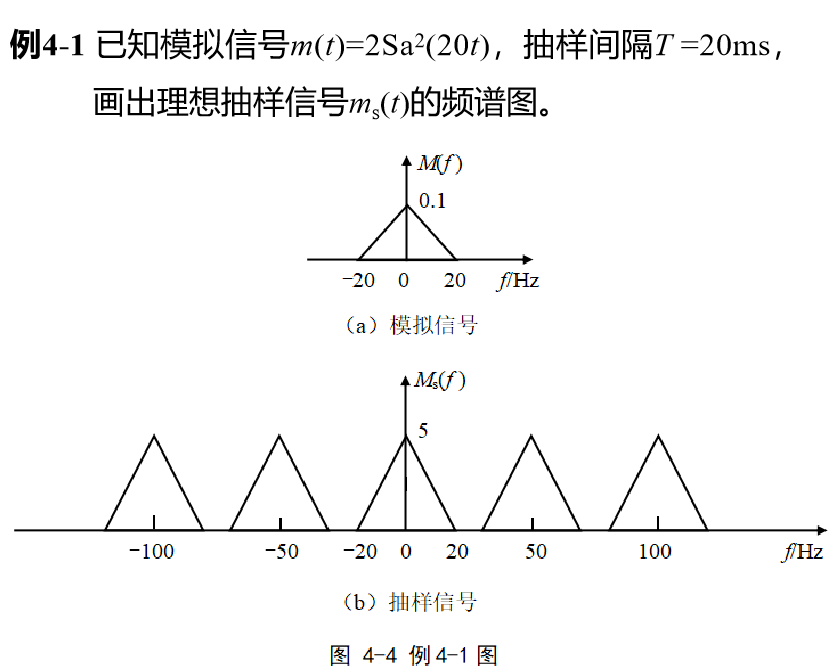
• 抽样信号的频谱是模拟信号频谱沿频率轴方向的周期重复

1.2 抽样定理

抽样定理的主要作用就是
确定合适的抽样频率，以避免频谱混叠，确保接收端能正确重构模拟信号

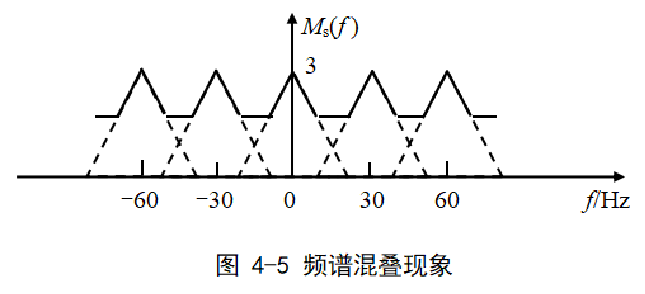
在实际系统中，根据被抽样的模拟信号特性，又分为低通和带通抽样定理。

低通抽样定理

带通抽样定理

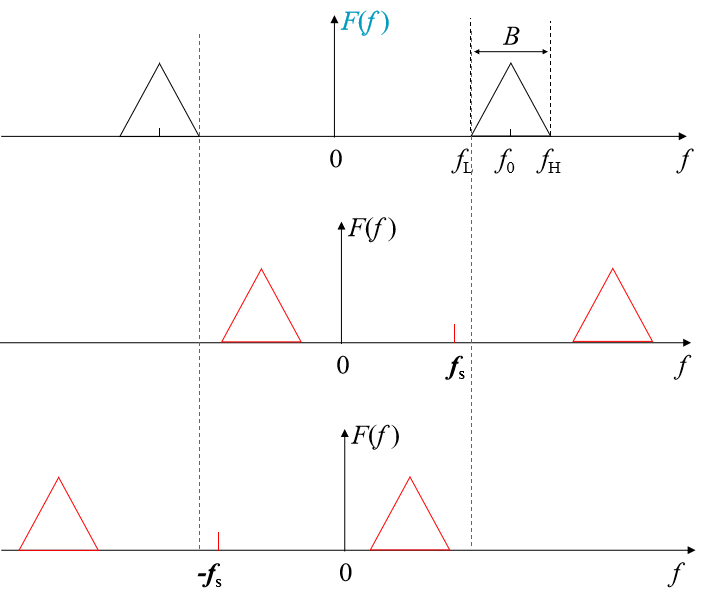
几点说明——

• 信号可以分为低通和带通两种，两种信号都可以分别根据低通和带通抽样定理确定抽样频率；
• 对低通信号，两个抽样定理确定的抽样频率相同；
  对带通信号，带通抽样时的抽样频率比低通抽样时更低；
• 低通抽样定理可以认为是带通抽样定理的特例；
• 低通和带通抽样的实现方法是一样的，只是根据两个抽样定理确定的抽样频率参数不同；
• 重构时，低通抽样必须用低通滤波器；带通抽样必须带通滤波器。

2 量化及量化信噪比

量化（Quantification） :抽样信号在各抽样时刻的幅度反映了模拟信号的幅度变化，因此仍然是连续的，必须在编码之前，将幅度抽样值用预先规定的有限个取值来表示。

• 实现量化的电路称为量化器。
• 量化器的输入为模拟信号的抽样值，输出称为量化电平。
• 抽样值与量化电平之间的关系称为量化特性，通常用量化特性曲线表示。

2.1 均匀量化

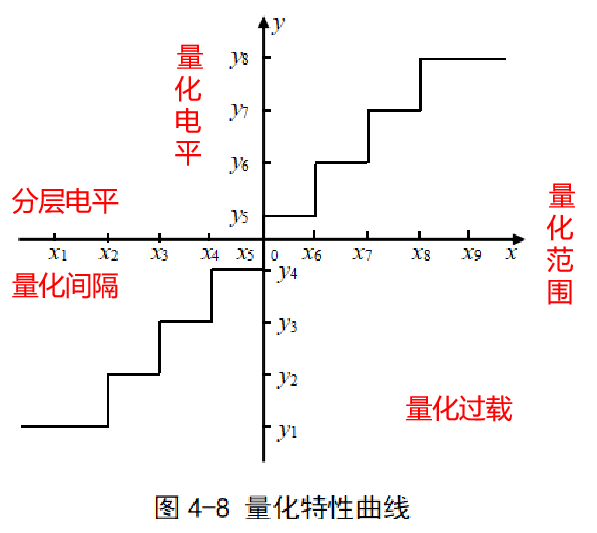
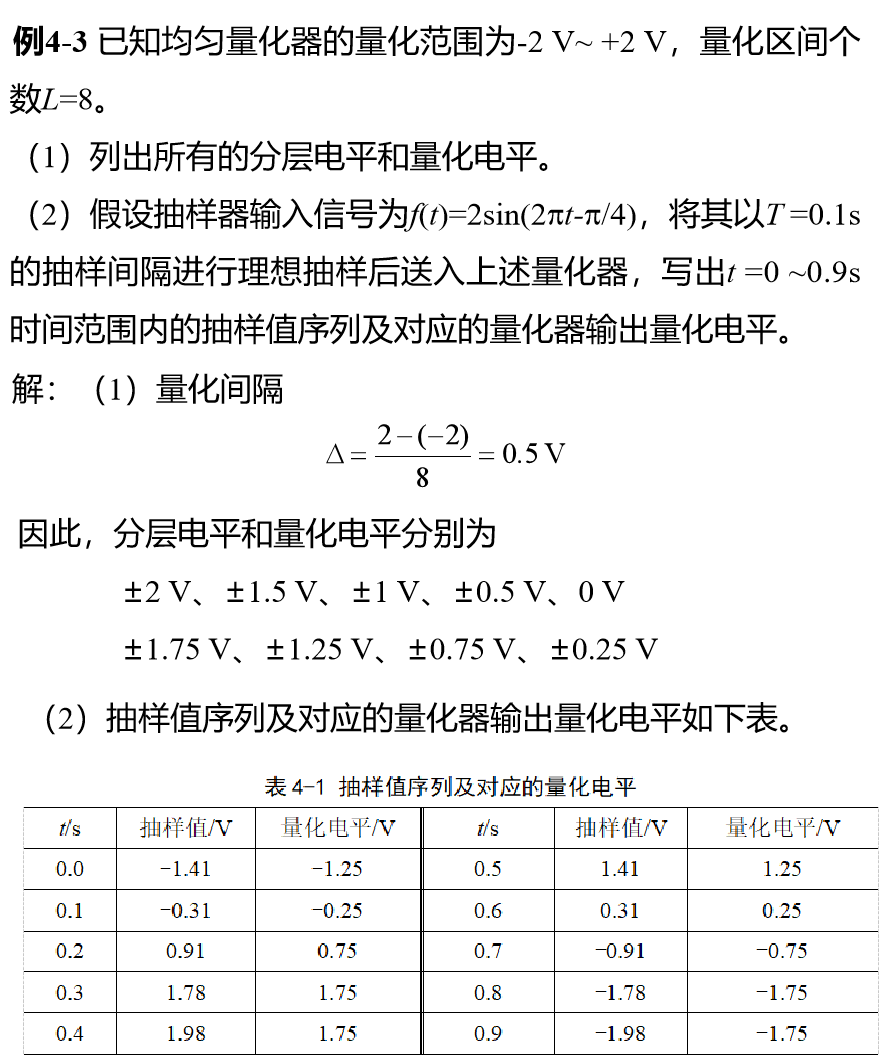
所有量化区间的量化间隔都相等，即将抽样值总的变化范围进行等分，称为均匀量化。否则称为非均匀量化。

2.2 量化误差和量化信噪比

• 量化误差
  量化器输出量化电平与输入抽样值之间存在误差，这种误差是由量化过程产生的，称为量化误差（量化噪声）。
  根据随机信号的相关知识，对量化间隔Δ足够小的均匀量化，在不过载的前提下，可以求得量化噪声的平均功率为
  
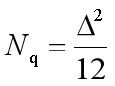
  量化噪声的功率只与量化间隔有关。一旦量化间隔给定，无论抽样值大小如何，量化噪声功率都保持不变。

• 量化信噪比
  量化信噪比描述的是量化误差相对于量化信号平均功率的大小，其具体定义为量化器输出量化信号的平均功率与量化噪声的平均功率之比。
  
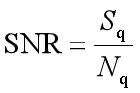
  量化信噪比与输入信号的功率成正比，与量化噪声的功率成反比。

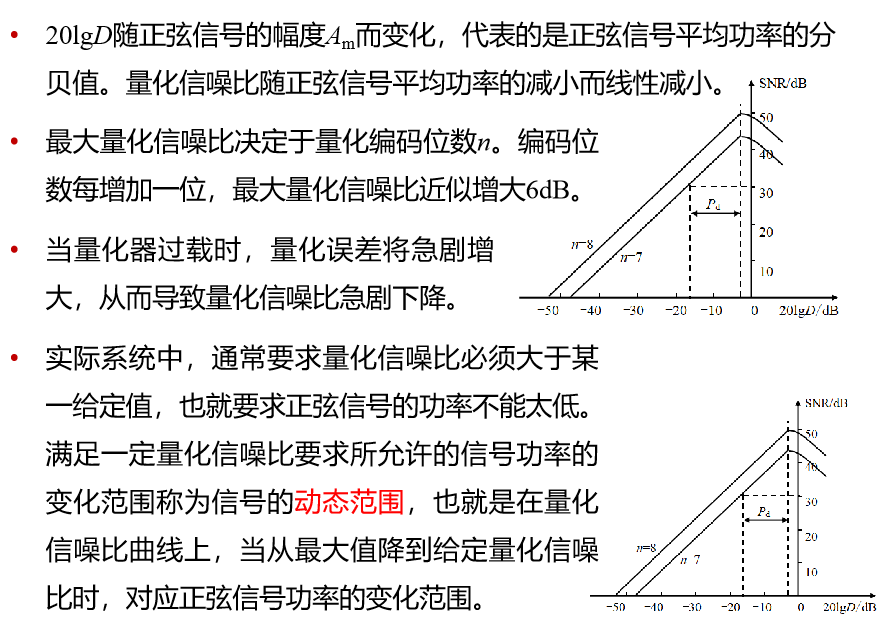
• 量化信噪比曲线
  量化信噪比与正弦信号的归一化功率20 lgD 和编码位数之间的关系曲线。
  

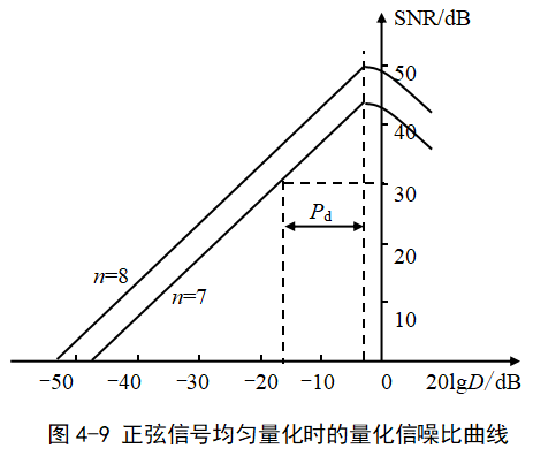
几点说明——

2.3 非均匀量化

对于均匀量化，量化噪声的平均功率都恒定不变，从而导致量化信噪比随信号功率的减小而减小。
当信号幅度过小时，量化信噪比太小。或者，为满足给定的量化信噪比要求，信号的动态范围不能满足实际系统的要求。
为保证当信号功率在足够宽的范围内变化时，量化信噪比都能满足要求，可以减小量化间隔，或者增加量化间隔数。但所需编码电路将变得复杂，并且对量化编码输出信号数字化传输性能的要求也将随之提高。
为了解决这一问题，提出了非均匀量化。

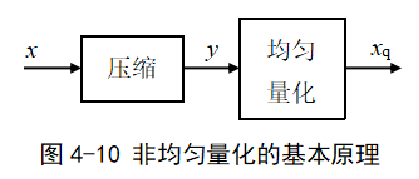
• 基本思想及实现原理
  当信号幅度比较小时，适当减小量化间隔，从而同步减小量化误差；当信号幅度大时，适当增大量化间隔，以避免量化级数和量化编码位数增加太多。
  实现原理:压缩-均匀量化；解码-扩张
  

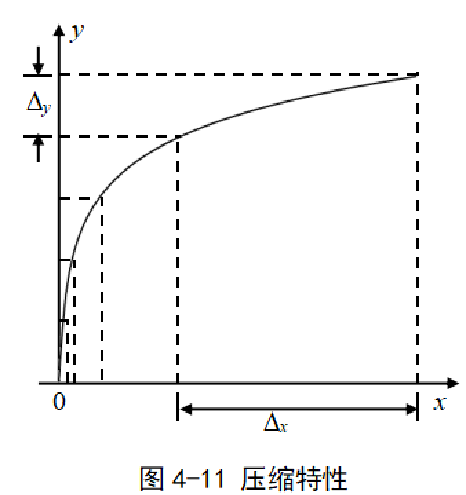
• 压缩特性（以A律压缩特性为例）
  
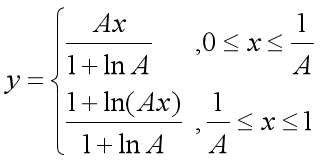
  式中，x 和 y 为压缩器输入输出电平的归一化值；
  A：压缩参数，表示压缩的程度。
  A越大，压缩效果越明显。在国际标准中取 A=87.6。
  

非均匀量化的量化信噪比
压缩特性是一条非线性曲线，曲线上各点具有不同的斜率，斜率的大小反应了采用非均匀量化时量化信噪比的改善量。

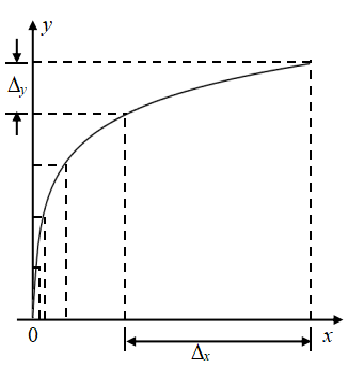
对于A>1的压缩特性，随着信号功率的减小，曲线斜率逐渐增大。因此，信号功率越小，对量化信噪比的改善量越大。
但是，随着信号功率增大，量化信噪比没有得到改善，甚至有一定程度的下降。

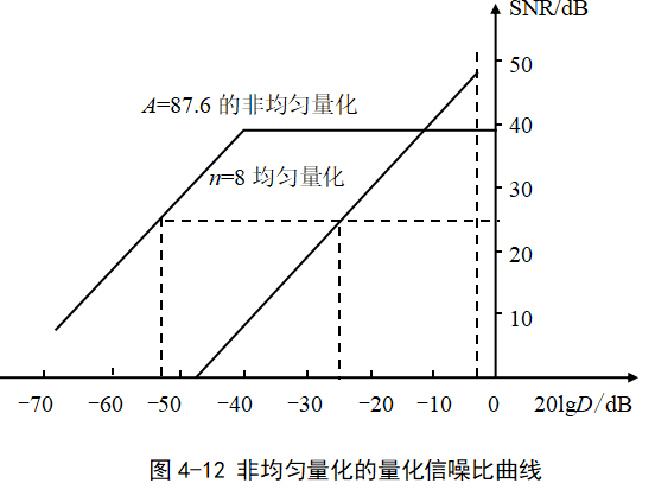
采用A=87.6的对数压缩特性，相对于n=8的均匀量化，动态范围扩大近似30dB。

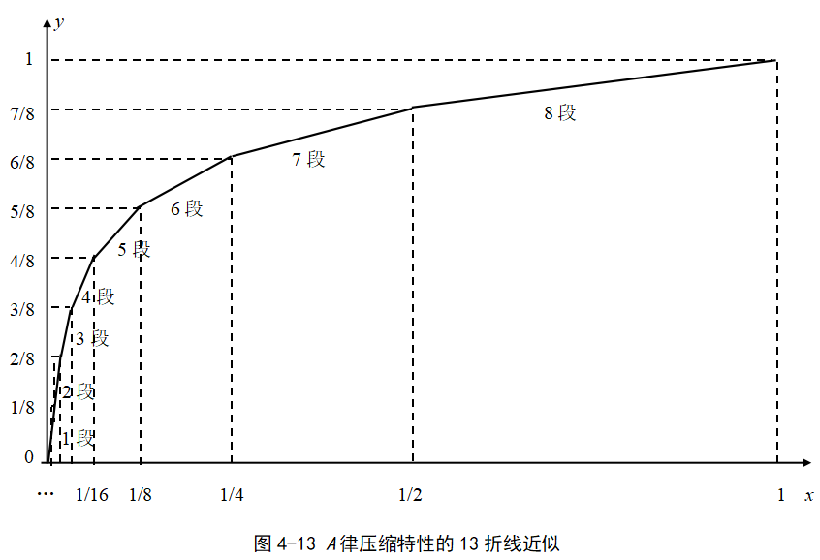
• A律压缩特性的13折线近似
  

3 编 码

编码（Coding）
所谓编码就是将量化器输出量化信号在各离散时刻的取值用指定位数的二进制代码表示，从而得到数字信号。

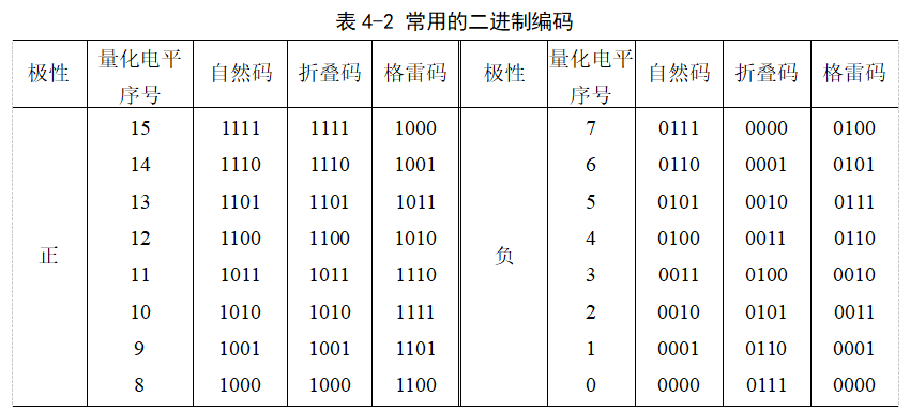
3.1常用的二进制码组

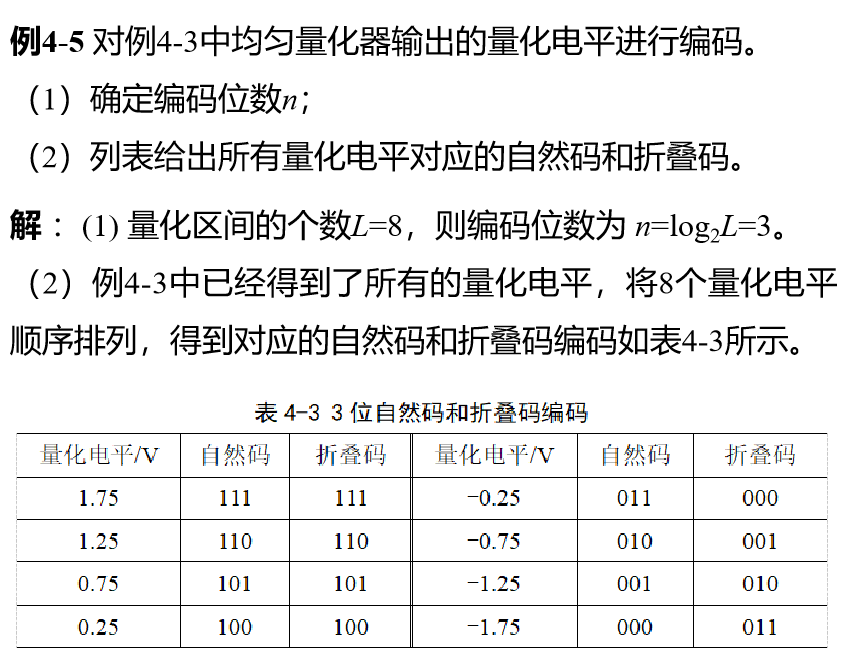
码字（Codeword）:基本的编码方法是将所有量化电平按大小排序，并为每个量化电平分配一个整数序号，再将各序号用指定位数的二进制代码表示。

根据各时刻送来模拟信号抽样值对应的量化电平，编码器输出相应的二进制代码码字。

根据各电平电平排序的方法及其与输出码字的对应关系，语音信号的编码方法常用的有自然码、折叠码和格雷码等。

3.2 均匀量化编码方法

• 自然码编码
  

• 折叠码编码
• 由抽样值x的正负确定最高位，0负1正；
• 计算|x|/Δ ，将商的整数部分转换为n-1位二进制代码;
• 与最高位拼起来得到 n 位编码。

3.3 A律13折线编码

A律13折线编码是专门针对A律压缩特性进行非均匀量化提出的一种非线性编码方法。
在这种编码方法中，将A律折线近似中的各段再等分为16个小的量化区间，每个小的量化区间对应一个量化电平，再对各量化电平进行编码。
显然，由于正负方向共有16段折线，因此总的量化电平数为1616=256，因此一共需要8位编码。

手工编码步骤
已知抽样值或量化电平x，具体步骤如下：

• 由x的正负确定极性码（0负1正）；
• 将|x|与各段落起始电平xi比较，确定段落码；
• 计算(|x|-xi)/Δi，其中Δi为第 i 段落中的量化间隔；
• 将商的整数部分转换为4位二进制得到段内码。
• 将极性码、段落码和段内码顺序排列在一起，得到8位A 律13折线近似编码。

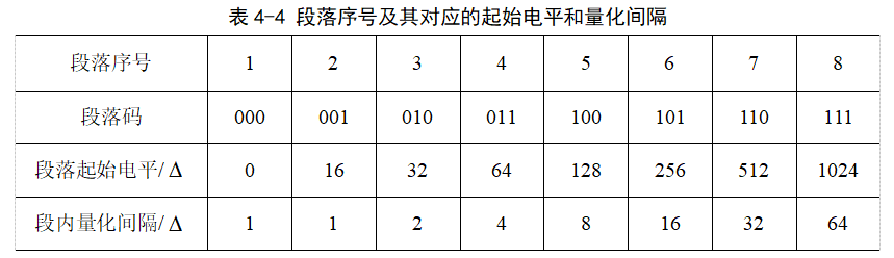
表中的各电平都用为单位，称为量化单位。
在8个段落中，第1和第2段落长度为归一化值的1/128，将其等分为16个小段后，得到的量化间隔等于
(1/128)×(1/16) = 1/2048 = 1Δ

4 脉冲编码调制系统

脉冲编码调制（PCM，Pulse-Code Modulation）

• 通过抽样、量化和编码将模拟信号转换为数字信号，这一过程可以认为是用模拟信号作为基带信号，以二进制脉冲序列作为载波，通过调制改变脉冲序列中各二进制码元的取值。
• 通过PCM编码调制输出的二进制代码序列称为PCM编码信号，编码输出信号经过数字通信系统传输到接收端后，解码（译码）得到量化信号，再由滤波器和频率失真补偿等电路即可重构原始模拟信号。

4.1 PCM系统的码元速率

抽样器每隔一个抽样间隔T 输出一个抽样值。通过量化编码，每个抽样值对应输出n位二进制代码。

结论：编码输出码元速率与抽样频率和量化编码位数都成正比关系。其中，抽样频率根据抽样定理确定，编码位数决定了量化误差和量化信噪比的大小。

4.2 PCM系统的抗噪声性能

影响PCM系统传输可靠性的主要噪声源有两种：一是量化噪声，二是信道噪声。

• 量化噪声
  量化噪声对传输系统的影响用量化信噪比来描述，量化信噪比随着编码位数按指数规律增加。也就是说，通过增加编码位数可以提高量化信噪比。
  但编码位数增加，编码输出的码元速率也随之增大。
  因此，PCM传输系统可以通过牺牲有效性换取传输可靠性的提高。

• 信道噪声
  信道噪声对PCM系统性能的影响表现在接收端的判决误码上。由于PCM信号中每一码字代表着一定的量化值，所以若出现误码，被恢复的量化值将与发端原抽样值不同，从而引起误差，形成输出噪声，即误码噪声。
  经分析可知，由信道噪声引起的平均误码噪声功率和误码信噪比分别为
  

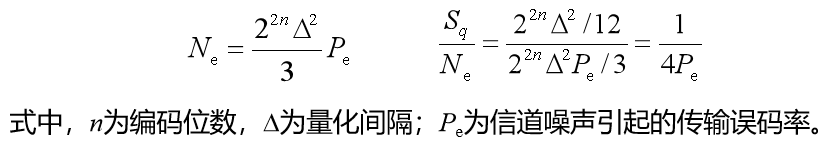
5 预测编码

在预测编码中，不是独立地对每个抽样值进行量化编码，而是根据前面若干个抽样值计算得到一个预测值，再与当前抽样值进行比较，对其差值（预测误差）进行编码。
对于语音等连续变化的信号，其抽样值之间具有一定的相关性，使得抽样值与预测值之间的预测误差非常小，远小于抽样值的变化范围。
因此，对预测误差进行编码，可以极大减少编码位数，从而降低编码输出码元速率。

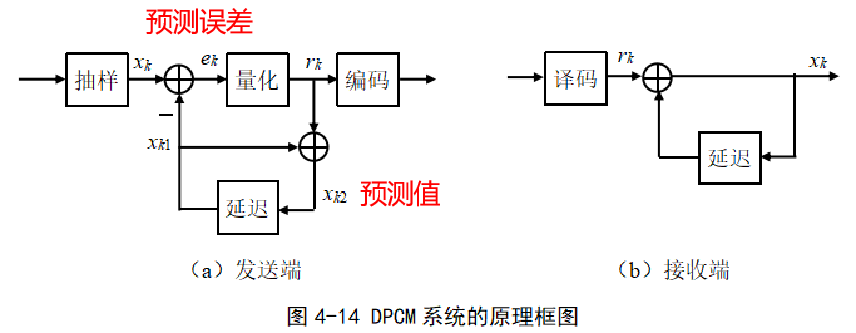
5.1 差分脉冲编码调制

差分脉冲编码（DPCM，Differential Pulse Code Modulation）就是利用语音信号的相关性，根据过去的信号抽样值预测当前时刻的抽样值，得到当前抽样值与预测值之间的差值，并对该预测误差进行量化编码。

5.2 增量调制

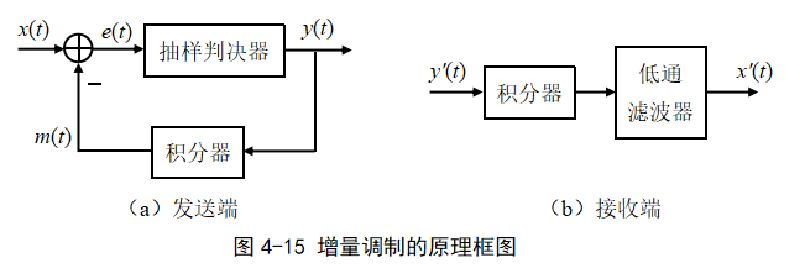
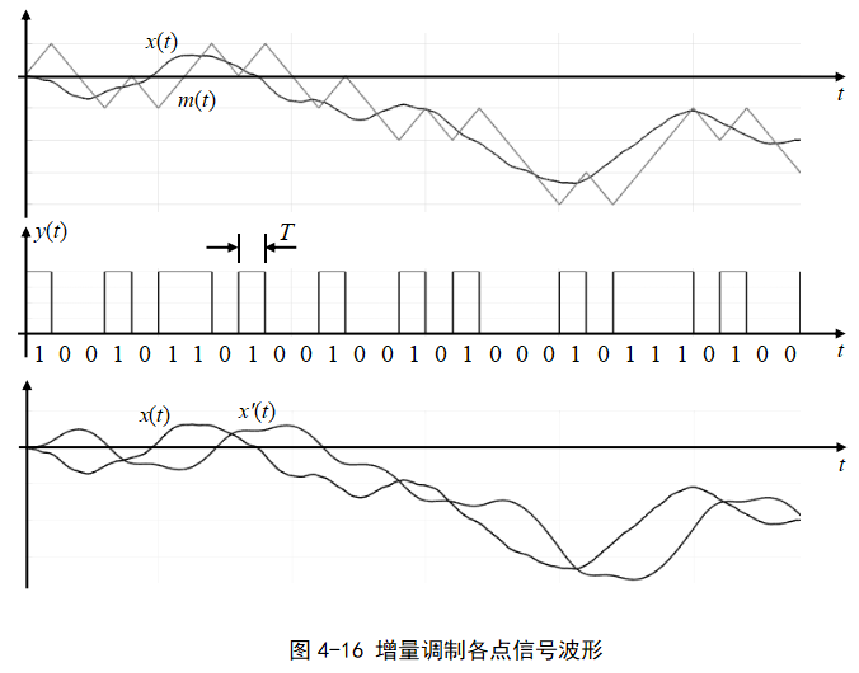
增量调制（DM或M，Delta Modulation）可以视为DPCM的一个特例，是一种两电平量化的差分脉冲编码调制。
在增量调制中，量化器的输出只有正负两个电平，经过编码后输出一位二进制代码。
实际系统中，增量调制的实现原理

6 时分复用和复接

6.1 时分复用的基本原理

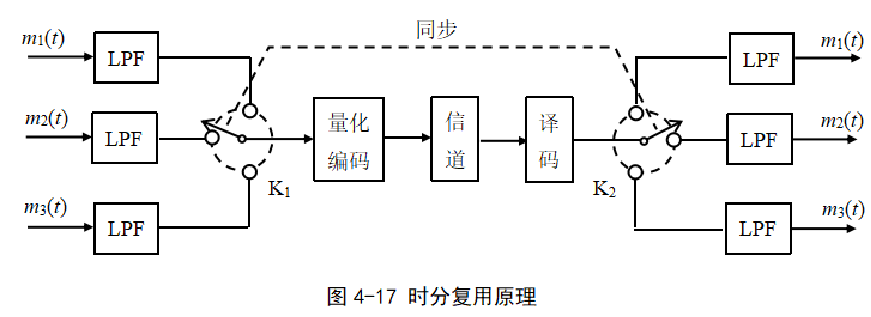
假设各路信号抽样频率为 fₛ，并令K₁旋转一周所需的时间等于抽样间隔T，每个T 间隔内，开关K₁依次将三路信号的一个抽样值在时间上错开，送入后面的量化编码器。
量化编码器每接收到一个抽样值，立即进行编码，并通过信道传输到接收端。
假设每个抽样值编码输出n位二进制，则在T（一帧）这段时间内，共编码输出 3n 位二进制。因此，通过时分复用后，量化编码输出的码元速率为 Rₛ = 3n/T = 3nfₛ。
推广到一般情况，假设共有m路信号进行时分复用，每路信号抽样频率为fs，量化编码位数为n，则码元速率为

6.2 复接

在通信网中，为了充分利用信道的传输能力，一般需要经过多级复用，由各链路送来的低级复用信号（低此群）可能需要再次进行复用，构成速率更高的高级复用信号（高此群）。这种将低次群合并为高次群的过程称为复接（Multiplexing）。
在数字复接系列中，根据传输速率的不同，将复用后的数据流分别称为基群（一次群）、二次群、三次群和四次群等。

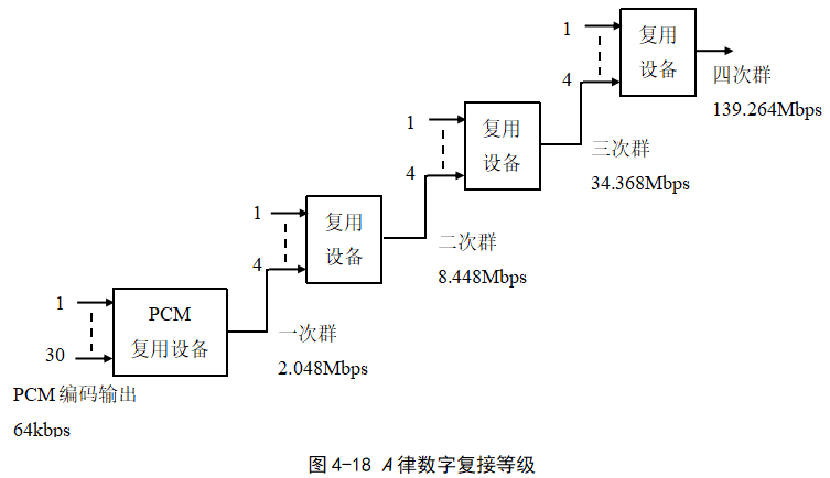
• PDH和SDH
  各路信号可能来自于不同地点，其抽样和编码时钟相互独立，不可能保持完全同步，因此在低次群合并为高次群时，需要将各路信号的时钟调整统一。
  这种复接技术称为准同步数字系列（PDH，Plesiochronous Digital Hierarchy）。
  对同步复接系列（SDH，Synchronous Digital Hierarchy）网络中各设备的时钟来自于同一个时间标准，没有定时误差。SDH具有同步复用、标准光接口和强大的网络管理能力等优点，逐渐在光纤、微波和卫星等多种通信系统中得到广泛应用。