一、概述

我们在上一章中已经对背包模型做了一定地讲解，但是我们发现其实在上一章节中我们所介绍的例题大部分是给背包问题套上一个背景，当我们识破了背后的模型后，我们就可以直接套用模板，基本不需要对代码做改变。

那么在这一章节中，我们将讲解一些在背包问题代码上做出一定改变的题目。比如求方案数，方案等等。

二、例题

1、AcWing 1020. 潜水员

（1）问题

（2）分析

这道题表面上是一个二维费用背包模型，但是在模型题目中，我们的状态f[i][j][k]表示的是体积至多是j，重量至多是k，也就是一个小于等于的大小关系。

但是这道题不一样，我们要保证氧气和氮气足量，也就说可以多不能少，那么如果用二维费用背包模型表达的话，即状态f[i][j][k]表示的是体积至少是j，重量至少是k，反而是一个大于等于的大小关系。

由于状态含义的改变，我们的代码一定会改变，这里还涉及到了下标为负数时的处理。作者在之前的文章中做过详细地讲解，大家可以去看一看：AcWing 1020. 潜水员（二维费用背包的变形）详解

（3）代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1010;
int n,m,k;
int o2[N],n2[N],w[N];
int f[N][30][80];
int main()
{
    cin>>m>>n>>k;
    for(int i=1;i<=k;i++)scanf("%d%d%d",o2+i,n2+i,w+i);
    memset(f,0x3f,sizeof f);
    f[0][0][0]=0;
    for(int i=1;i<=k;i++)
    {
        for(int j=0;j<=m;j++)
        {
            for(int p=0;p<=n;p++)
            {
                f[i][j][p]=f[i-1][j][p];
                int m1=min(j,o2[i]),m2=min(p,n2[i]);
                f[i][j][p]=min(f[i-1][j-m1][p-m2]+w[i],f[i][j][p]);
            }
        }
    }
    cout<<f[k][m][n]<<endl;
    return 0;
}

2、AcWing 7. 混合背包问题

（1）问题

（2）分析

这道题则是各种背包问题的融合，只有大家掌握了各种单一的背包问题才能来解决这道题，但是如何将各种问题融合起来则是这道题的难点。也需要我们对代码模板做一定的改变和拼接。

详解请看：混合背包问题详解

（3）代码

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=2e4+10;
int f[N];
int n,m,v,w,s;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d%d",&v,&w,&s);
        if(!s)
        {
            for(int j=v;j<=m;j++)
                f[j]=max(f[j],f[j-v]+w);
        }
        else
        {
            if(s==-1)s=1;
            int k;
            for(k=1;k<=s;k*=2)
            {
                for(int j=m;j>=k*v;j--)
                {
                    f[j]=max(f[j],f[j-k*v]+k*w);
                }
                s-=k;
            }
            if(s)
            {
                for(int j=m;j>=s*v;j--)
                {
                    f[j]=max(f[j],f[j-s*v]+s*w);
                }
            }
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

3、AcWing 12. 背包问题求具体方案

（1）问题

（2）分析

这道题也是求方案数，但是为了满足题目中最小字典序的条件，我们需要更改状态转移方程中的状态定义。这一点是比较难的。作者在之前的文章中做过介绍，不懂的同学可以去看一看：AcWing 12. 背包问题求具体方案

（3）代码

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1010;
int v[N],w[N],f[N][N],cnt[N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)scanf("%d%d",v+i,w+i);
    for(int i=n;i>=1;i--)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i+1][j];
            if(j>=v[i])f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
        }
    }
    int j=m;
    int count=0;
    for(int i=1;i<=n;i++)
        if(j>=v[i]&&f[i+1][j-v[i]]+w[i]==f[i][j])
        {
            cout<<i<<" ";
            j-=v[i];
        }

    return 0;
}

4、AcWing 11. 背包问题求方案数

（1）问题

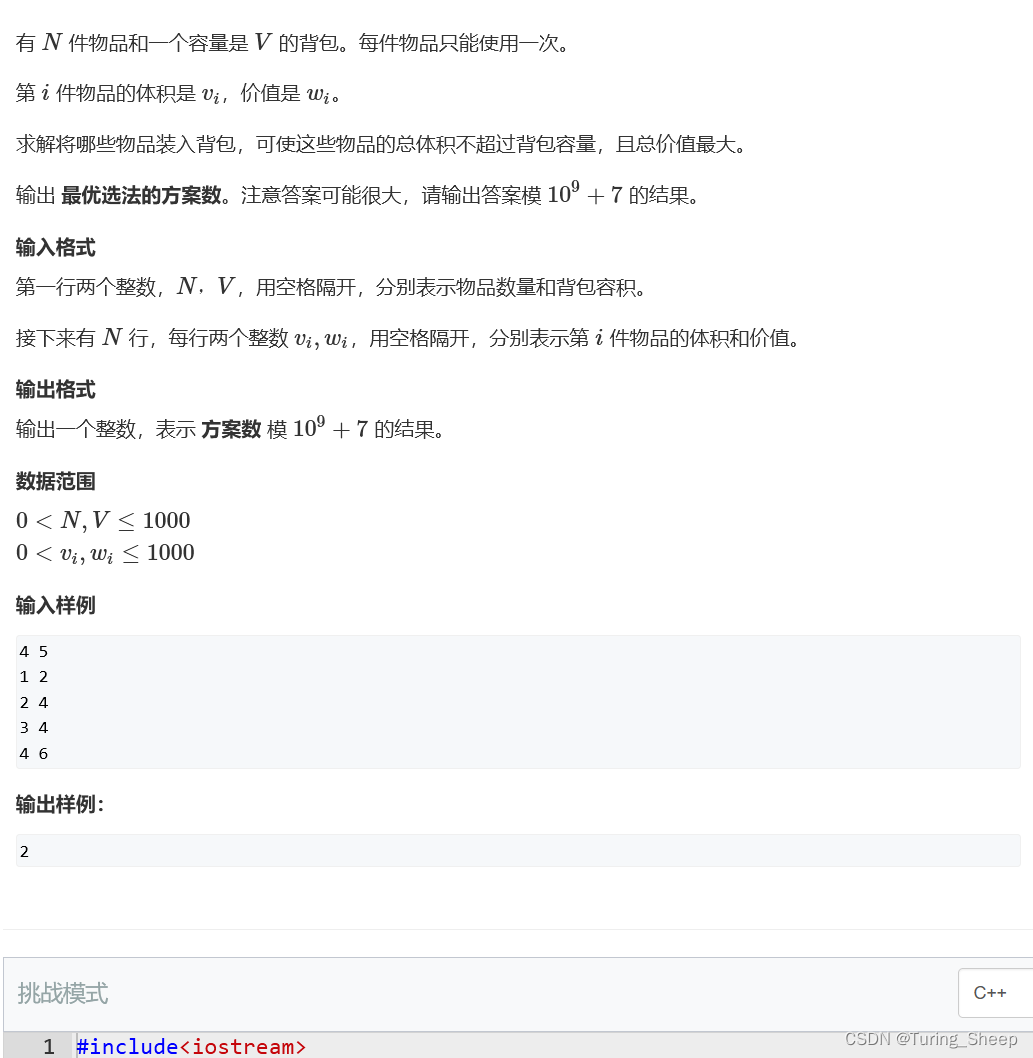
（2）分析

这道题也是求方案，但是这次求的时方案数目，而这个过程也是一个DP，而这个DP的书写则需要用01背包的思路来写。所以这道题是利用背包问题的思想去解决新的问题，详解请看：
AcWing 11. 背包问题求方案数

（3）代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1010,mod=1e9+7;
int f[N],g[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=0;i<=m;i++)g[i]=1;
    for(int i=1;i<=n;i++)
    {
        int v,w;
        cin>>v>>w;
        for(int j=m;j>=v;j--)
        {
            if(f[j]<f[j-v]+w)
            {
                g[j]=g[j-v];
                f[j]=f[j-v]+w;
            }
            else if(f[j]==f[j-v]+w)
                g[j]=(g[j]+g[j-v])%mod;
        }
    }
    cout<<g[m]<<endl;
    return 0;
}

5、AcWing 1013. 机器分配

（1）问题

（2）分析

这道题是分组背包的应用，以及在分组背包的条件下如何求方案的问题，详解请看：AcWing 1013. 机器分配（分组背包问题与方案记录）

（3）代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=15,M=20;
int f[N][M],v[N][M],w[N][M];
int way[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&w[i][j]);
            v[i][j]=j;
        }
    
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            for(int k=0;k<=m;k++)
            {
                if(j>=v[i][k])
                f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);
            }
        }
    }
    
    cout<<f[n][m]<<endl;
    int j=m;
    for(int i=n;i>=1;i--)
    {
        for(int k=0;k<=m;k++)
        {
            if(j>=v[i][k]&&f[i][j]==f[i-1][j-v[i][k]]+w[i][k])
            {
                way[i]=k;
                j-=k;
                break;
            }
        }
    }
    for(int i=1;i<=n;i++)cout<<i<<" "<<way[i]<<endl;   
    return 0;
}