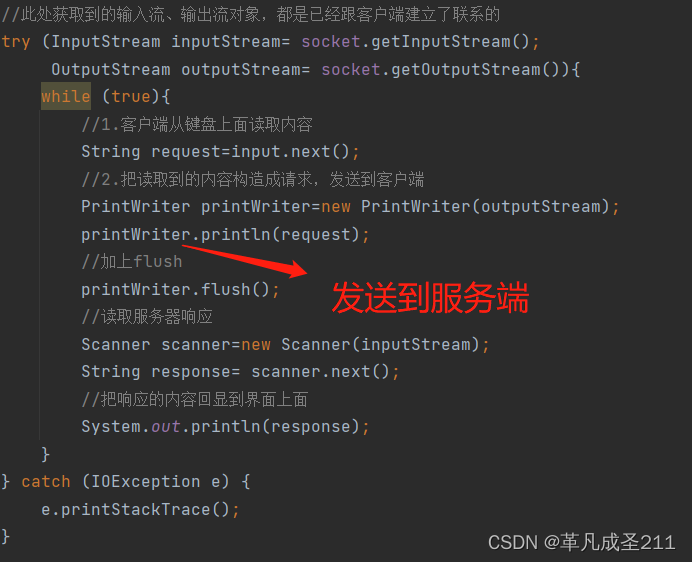
题目

T(T<=5e3)组样例，每次给定一个数n(n<=5e3)，

和长为n的两个数组a,b，你可以执行以下操作任意次：

操作：选择一个下标i(1<=i<=n)，将替换为，其中被认为是

问若干次操作后，a和b能否完全相同，可以输出Yes，不能输出No

思路来源

灵茶群

题解

注意到需要初始局面至少有一个元素相等，

所以本能的想法是枚举初始点，然后往前或往后暴力赋值，

赋ai的时候，只考虑ai原来的值、ai+1原来的值，ai+1后来被赋的值

但是，这个做法是假的，赛中会一直ac26wa34，

考虑以下样例，相同的数字段，实际是可以循环移位，越过原来的位置的

6
1 1 1 2 1 3
1 3 2 2 2 2

根据能平移，衍生成了题解的做法：

将a和b分别看成环，并尺取相同值的段去重，得到新的数组a'和b'

1. b'的长度为n，说明a'的长度也得为n，且和原来的元素一一对应

2. b'长度小于n，说明b的总种类数小于n，说明a最终总种类数小于n即可，

则a'至少可以执行一次操作，覆盖掉一个元素，有一个空位后，则可以执行循环移位操作，

比如，1123->1223->1233->2311

支持了这样的循环移位后，只需要b’是a'循环移位条件下的子序列即可

因为a'支持两种操作，一种是循环移位，另一种是赋值覆盖，覆盖掉不想要的元素种类

代码

#include<iostream>
#include<vector>
using namespace std;
const int N=5e3+10,mod=998244353;
int T,n,c[N],d[N];
vector<int>a,b;
void calc(int *x,vector<int>&y){
    y.clear();
    int las=-1;
    for(int i=0;i<n;++i){
        cin>>x[i];
        if(x[i]!=las)y.push_back(x[i]);
        las=x[i];
    }
    if(y.size()>1 && y.back()==y[0])y.pop_back();
}
bool solve(){
    int sa=a.size(),sb=b.size();
    if(sb==n)return a==b;
    for(int i=0;i<sa;++i){
        int cur=0;
        for(int j=0;j<sa;++j){
            if(b[cur]==a[(i+j)%sa])cur++;
            if(cur==sb)return 1;
        }
    }
    return 0;
}
int main(){
    cin>>T;
    while(T--){
        cin>>n;
        calc(c,a);calc(d,b);
        cout<<(solve()?"Yes":"No")<<endl;
    }
    return 0;
}
/*
2
4
1 1 2 3
2 3 3 3
6
1 1 1 2 1 3
1 3 2 2 2 2
*/