一、前言

本文主要讲了线段树的Lazy-tag技术和一道例题，建议自己要多练习线段树的题目。

二、Lazy-tag技术

背景：区间修改
简单区间修改，例如对一个数列的 [L, R] 区间内每个元素统一加上 d。
如果在线段树上用 “单点修改” 一个个修改这些元素，一次区间修改O(nlogn)，还不如直接暴力修改的 O(n)。
解决办法，利用线段树的特征：线段树的结点 tree[i]，记录了 i 这个区间的值。
再定义一个 tag[i]，用它统一记录 i 这个区间的修改，而不是一个个修改区间内的每个元素。
这个办法被称为 “lazy-tag”。一次区间修改 O(logn)。

lazy-tag (懒惰标记，或者延迟标记)。
修改一个线段区间时，只对这个线段区间进行整体修改 (把修改记录在子树的根结点上)，其内部每个元素的内容先不做修改。
当这个线段区间的一致性被破坏时，才把变化值传递给下一层。
复杂度：每次区间修改的复杂度是 O(logn) 的。

1、update() 中的lazy-tag

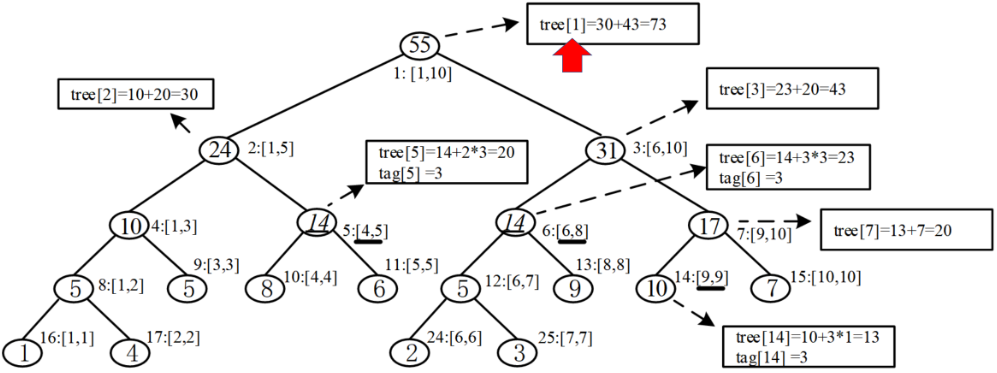
例：把 [4, 9] 区间内的每个元素加 3：

1）左子树递归到结点 5，即区间 [4, 5]，完全包含在 [4, 9] 内，打标记 tag[5] = 3，更新 tree[5] 为 20，不再继续深入；

2）左子树递归返回，更新 tree[2] 为 30；

3）右子树递归到结点 6，即区间 [6, 8]，完全包含在 [4, 9] 内，打标记 tag[6]=3，更新 tree[6] 为 23。

4）右子树递归到结点 14，即区间 [9, 9]，打标记 tag[14]=3，更新 tree[14]=13；

5）右子树递归返回，更新 tree[7]=20；继续返回，更新 tree[3]=43；

6）返回到根结点，更新 tree[1]=73。

【多次修改】

如果发生多次修改同一个结点上的 tag 会发生多次修改，导致冲突。
例如做 2 次区间修改，一次是 [4, 9]，一次是 [5, 8]，它们都会影响 5:[4, 5] 这个结点。

第一次修改 [4, 9] 覆盖了结点 5，用 tag[5] 做了记录；

第二次修改 [5, 8] 不能覆盖结点 5，需要再向下搜到结点 11:[5, 5]，从而破坏了 tag[5]，此时原 tag[5] 记录的区间统一修改就不得不往它的子结点传递和执行了，传递后 tag[5] 失去了用途，需要清空。

【push_down】

lazy-tag 的主要操作是解决多次区间修改的冲突，用 push_down() 函数完成。它首先检查结点 p 的 tag[p]，如果有值，说明前面做区间修改时给 p 打了 tag 标记，接下来就把 tag[p] 传给左右子树，然后把 tag[p] 清零。push_down() 函数不仅在 “区间修改” 中用到，在 “区间查询” 中同样用到。

三、例题

1、区间修改、区间查询（lanqiaoOJ 1133）

注：该题用树状数组讲过

【题目描述】

给定一个长度为 N 的数组 a，初值为 a1, a2, ..., aN

有 Q 个操作，操作有两种：

1 L R d：将区间 [L,R] 内每个数加上 d。

2 L R：输出区间 [L, R] 内每个数的和。

【输入描述】

第 1 行是整数 N、M，表示数组 a 的长度和操作个数。1<=n, m<=10^5

第 2 行包含 N 个非负整数 a1, a2, ..., aN，表示数组 a 的初值

第 3~M-2 行每行表示一个操作

【输出描述】

输出每行一个整数，表示查询的答案

【输入样例】

5 5

1 2 3 4 5

2 1 2

1 2 3 1

2 1 3

1 1 5 1

2 1 5

【输出样例】

3

8

22

【完整代码】

def bulid(p,pl,pr):     #建树
    if pl==pr:
        tree[p]=a[pl]
        return
    mid=(pl+pr)>>1
    bulid(p<<1,pl,mid)
    bulid(p<<1|1,mid+1,pr)
    tree[p]=tree[p<<1]+tree[p<<1|1]     #push_up(p)

def addtag(p,pl,pr,d):       #给结点p打tag标记,并更新tree
    tag[p]+=d               #打上tag标记
    tree[p]+=d*(pr-pl+1)    #计算新的tree

def push_down(p,pl,pr):
    if tag[p]>0:            #有tag标记，这是以前做区间修改时留下的
        mid=(pl+pr)>>1
        addtag(p<<1,pl,mid,tag[p])      #把tag标记传给左子树
        addtag(p<<1|1,mid+1,pr,tag[p])  #将tag标记传给右子树
        tag[p]=0                        #p自己的tag被传走了

def update(L,R,p,pl,pr,d):
    if L<=pl and pr<=R:     #在这个区间里面
        addtag(p,pl,pr,d)
        return
    push_down(p,pl,pr)  #将懒惰标记传递给孩子.tree[p]不能完全被包含在需要修改的区间[L,R]中，需要解决多次修改的冲突问题
    mid=(pl+pr)>>1
    if L<=mid:
        update(L,R,p<<1,pl,mid,d)
    if R>=mid+1:
        update(L,R,p<<1|1,mid+1,pr,d)
    tree[p]=tree[p<<1]+tree[p<<1|1]     #push_up(p)

def query(L,R,p,pl,pr):
    if L<=pl and pr<=R:
        return tree[p]
    push_down(p,pl,pr)
    res=0
    mid=(pl+pr)>>1
    if L<=mid:
        res+=query(L,R,p<<1,pl,mid)
    if R>mid:
        res+=query(L,R,p<<1|1,mid+1,pr)
    return res

n,m=map(int,input().split())
a=[0]+list(map(int,input().split()))
tag=[0]*(len(a)<<2)      #4倍大
tree=[0]*(len(a)<<2)
bulid(1,1,n)            #建树
for i in range(m):
    w=list(map(int,input().split()))
    if len(w)==3:       #区间查询:[L,R]的区间和
        q,L,R=w
        print(query(L,R,1,1,n))
    else:               #区间修改:把[L,R]的每个元素加上d
        q,L,R,d=w
        update(L,R,1,1,n,d)

1）build(）建树

2）update() 函数更新区间的值，把区间内所有元素的值加上 d。如果 tree[p] 这棵子树完全被包含在需要修改的区间 [L, R] 中，只需要对根 tree[p] 打上标记即可，不用修改 p 的子结点。

3）addtag() 打标记

4）update() 中的 push_down。update() 函数更新区间的值，把区间内所有元素的值加上 d。如果 tree[p] 这棵子树不能完全被包含在需要修改的区间 [L,R] 中，需要解决多次修改的冲突问题，用 push_down() 实现。

解决 tag 的冲突问题。把 tag 分别传给左右子树。

注意：tag 应该持续向下传递，直到能覆盖区间为止。但是 push_down() 只向下传递了一次。因为使用 push_down() 的 update() 是个递归函数，update() 会在递归时一层层地用 push_down() 来传递 tag。

5）query() 查询区间和。查询时用到 tag，也就是用 push_down() 来处理 tag。

【总结】