回归损失与分类损失

回归用于逼近某个数值，预测的结果是连续的，例如预测小明的身高，160,161,162,163cm。平方损失即MSE：

分类用于预测物体属于某一个标签，预测的结果是离散的，例如预测明天是否下雪：是or否。
由于预测分类，最终的输出需要介于（0,1）之间，通常在网络输出处接上sigmoid或softmax （因为其函数值域在（0,1）之间）。
一个最常见的问题就是：为什么分类任务要用交叉熵损失函数，而不用均方误差损失函数？详细推导看到这里，我直接给出结论。
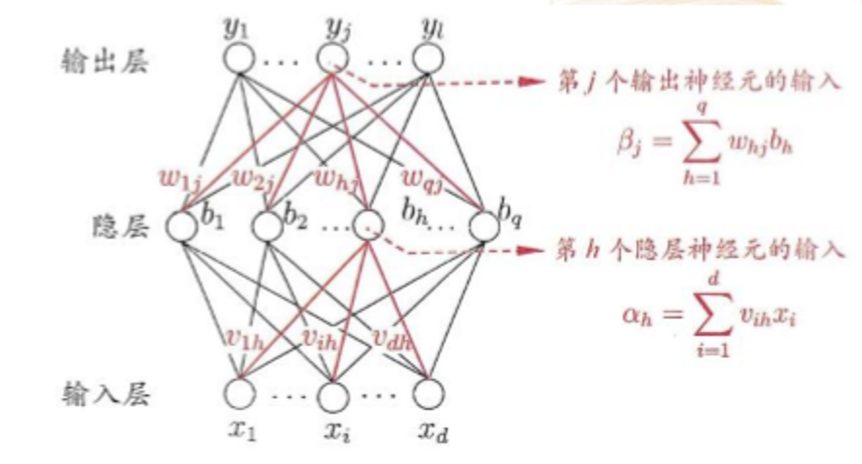
这与他们的导数形式是相关的，当接平方损失时：求得权重w与偏置b的梯度如下：

σ’(z)表示sigmoid或softmax的梯度，其梯度在网络输出概率接近0或1时非常小。
对于交叉熵损失函数：
其梯度为: 梯度的大小与网络输出概率值和期望值的差相关，差别越大，梯度越大，这是一个很好的性质。

log 损失
分类