二进制枚举子集

a&1 == 1 判断是否为奇数，如果为1，则为奇数因为奇数二进制末位一定是1，所以 与1 得到的结果是1

例

这里，1<<14——2¹⁴——第15位是1，可以表示14个1
i&（1<<j）—— 从0开始是因为，原本第1位就是1。所以j=0时，对应的就是 i 的最低位

状态压缩

旅行商问题

Floyd算法：

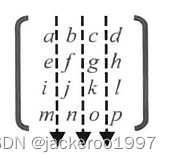
方格取数问题

now | flag == flag —— （1代表可以选择，0代表不可以选择）：

10110
00110
= 10110 == flag

10110
01001
= 11111 != flag

使用条件

• 状态需要有一定的状态单元。 即一个状态应该是保存一个集合，其中的元素值对应着0或1，例如我们常见的棋盘，我们可以用0或1来表示棋子的放置状态。而整个集合即是一个01串，即二进制数，我们通常用十进制表示。那么我们再进行状态转移或者判断的时候，需要先将十进制转化为二进制，再将二进制转化为十进制
• 题目中限制的集合大小不会超过20。 如果用二进制表示状态，那么集合大小为20的二进制状态有2²⁰-1，已经达到1e7的数量级了
• 具有动态规划的特性。 对于动态规划，一般都是要求最优化某个值，具有最优子结构的性质。同时也需要满足状态转移的特性，而不是前一个状态毫无关系的

[SCOI2005] 互不侵犯

在N×N的棋盘里面放K个国王，使他们互不攻击，共有多少种摆放方案。国王能攻击到它上下左右，以及左上左下右上右下八个方向上附近的各一个格子，共8个格子。

输入格式

只有一行，包含两个数N，K （ 1 <=N <=9, 0 <= K <= N * N）

输出格式

所得的方案数

样例输入 #1

3 2

样例输出 #1

16

思路

• 还是比较模板的一道题
• 国王的意思是：选定了格子，然后不能相邻（斜上方、斜下方）。跟方格取数差不多
• 首先对第1行进行处理，这样后面的行才能使用模板
• 循环模板：1. 枚举行。——2. 枚举上个阶段放了的国王数。——3. 枚举本阶段的状态。——4. 在枚举本阶段状态的同时，枚举上一阶段的状态，维护状态。

题解

#include<bits/stdc++.h>
using namespace std;
long long ans,n,m,k,f[10][100][1<<9+5];
int lowbit(int x){
	int tmp=0;
	while(x) tmp++,x-=x&(-x);
	return tmp;
}
int main(){
	scanf("%lld%lld",&n,&k);
	m=(1<<n)-1;
	for(int i=0;i<=m;++i){
		if(!(i&(i<<1))&&lowbit(i)<=k) 
		f[1][lowbit(i)][i]=1;
	} 
	//处理出第一行的所有情况 
	for(int i=2;i<=n;++i)//枚举行 
	for(int j=0;j<=k;++j)//枚举上个阶段放了的国王数 
	for(int x=0;x<=m;++x){//枚举本阶段的状态 
		if(x&(x<<1)) continue;//本阶段不能互相伤害 
		for(int y=0;y<=m;++y){//枚举上一个阶段的状态 
			if(x&y||x&(y<<1)||x&(y>>1)) continue;//本状态和上一个状态不能冲突
			if(j+lowbit(x)>k) continue;//本状态新放的国王数目+上个阶段国王数小于k 
			f[i][j+lowbit(x)][x]+=f[i-1][j][y];  //本状态加上一状态数 
		}
	}
	for(int j=0;j<=m;++j) ans+=f[n][k][j];
	printf("%lld",ans);
}

[NOI2001] 炮兵阵地

司令部的将军们打算在 $N\times M$ 的网格地图上部署他们的炮兵部队。

一个 $N\times M$ 的地图由 $N$ 行 $M$ 列组成，地图的每一格可能是山地（用 $\text{H}$ 表示），也可能是平原（用 $\text{P}$ 表示），如下图。

在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。

图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。

现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入格式

第一行包含两个由空格分割开的正整数，分别表示 $N$ 和 $M$。

接下来的 $N$ 行，每一行含有连续的 $M$ 个字符，按顺序表示地图中每一行的数据。

输出格式

一行一个整数，表示最多能摆放的炮兵部队的数量。

样例输入 #1

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

样例输出 #1

6

提示

对于 $100\%$ 的数据，$N\le 100$，$M\le 10$，保证字符仅包含 P 与 H。

思路

• 这道题还是有些复杂的
• 按照思路：1. 初始化（对第1行操作、枚举合法状态）。2. 状态转移。（循环判断后面的行是否合法——判断 i-1,i-2）

题解

#include<bits/stdc++.h>
using namespace std;
int n,m,num[60];
char s[110][15]; 
int rec[110];
int state[70],top;
int dp[110][70][70];
int main(){
	scanf("%d%d",&n,&m);
	for(int i=0;i<(1<<m);i++){
		if((i&(i<<1)||(i&(i<<2))))continue; 
		int k=i;
		while(k){
			++num[top];
			k&=(k-1);
		}
		state[top++]=i;
	}
	for(int i=0;i<n;i++){
		cin>>s[i];
		for(int j=0;j<m;j++)
			if(s[i][j]=='H')
		 	rec[i]|=(1<<j); 
	}
	for(int i=0;i<top;i++) {
		if(state[i]&rec[0])continue;
		dp[0][0][i]=num[i];
	}
	for(int i=1;i<n;i++){
		for(int j=0;j<top;j++) {
			if(state[j]&rec[i])continue; 
			for(int k=0;k<top;k++) {
				if(state[j]&state[k])continue;
				for(int t=0;t<top;t++) {
					if(state[j]&state[t])continue; 
					if(state[k]&state[t])continue;
					dp[i][k][j]=max(dp[i][k][j],dp[i-1][t][k]+num[j]); 
				}
			}
		}
	}
	int ans=0;
	for(int i=0;i<n;i++)
		for(int j=0;j<top;j++)
			for(int k=0;k<top;k++)
				ans=max(ans,dp[i][j][k]);
	printf("%d",ans);
}

[USACO06NOV]Corn Fields G

Farmer John has purchased a lush new rectangular pasture composed of M by N (1 ≤ M ≤ 12; 1 ≤ N ≤ 12) square parcels. He wants to grow some yummy corn for the cows on a number of squares. Regrettably, some of the squares are infertile and can’t be planted. Canny FJ knows that the cows dislike eating close to each other, so when choosing which squares to plant, he avoids choosing squares that are adjacent; no two chosen squares share an edge. He has not yet made the final choice as to which squares to plant.

Being a very open-minded man, Farmer John wants to consider all possible options for how to choose the squares for planting. He is so open-minded that he considers choosing no squares as a valid option! Please help Farmer John determine the number of ways he can choose the squares to plant.

农场主 $\mathrm{John}$ 新买了一块长方形的新牧场，这块牧场被划分成 $M$ 行 $N$ 列 $(1\le M\le 12;1\le N\le 12)$，每一格都是一块正方形的土地。 $\mathrm{John}$ 打算在牧场上的某几格里种上美味的草，供他的奶牛们享用。

遗憾的是，有些土地相当贫瘠，不能用来种草。并且，奶牛们喜欢独占一块草地的感觉，于是 $\mathrm{John}$ 不会选择两块相邻的土地，也就是说，没有哪两块草地有公共边。

$\mathrm{John}$ 想知道，如果不考虑草地的总块数，那么，一共有多少种种植方案可供他选择？（当然，把新牧场完全荒废也是一种方案）

输入格式

第一行：两个整数 $M$ 和 $N$，用空格隔开。

第 $2$ 到第 $M+1$ 行：每行包含 $N$ 个用空格隔开的整数，描述了每块土地的状态。第 $i+1$ 行描述了第 $i$ 行的土地，所有整数均为 $0$ 或 $1$ ，是 $1$ 的话，表示这块土地足够肥沃，$0$ 则表示这块土地不适合种草。

输出格式

一个整数，即牧场分配总方案数除以 $100,000,000$ 的余数。

样例输入 #1

2 3
1 1 1
0 1 0

样例输出 #1

9

思路

• f[i][j]表示在前i行中（包括i）在j个状态下的最大方案数，f[i][j]=(f[i][j]+f[i-1][k])
• 判断枚举出的状态是否符合题目要求
• 先对第1行进行初始化

题解

#include<bits/stdc++.h>
typedef long long ll;
const int p=100000000;
using namespace std;
int M,N,a[13][13],check[1<<12],ans=0;
ll f[13][1<<12],F[13];
int main(){
    scanf("%d%d",&M,&N);
    for(int i=1;i<=M;++i) for(int j=1;j<=N;++j) scanf("%d",&a[i][j]);
    for(int i=1;i<=M;++i) for(int j=1;j<=N;++j) F[i]=(F[i]<<1)+a[i][j]; //将第i行的可不可以种草的01状态用F[i]表示
    for(int i=0;i<(1<<N);++i){
        if(!(i&(i>>1))&&!(i&(i<<1))){
            check[i]=1; //记录合法状态，避免后面重复检测
            if((i&F[1])==i) f[1][i]=1; //i&F[i]==i，相同的情况：F[i]中的1≥i（二进制），也就是i——可以种草但不种。
        }
    }
    for(int i=2;i<=M;++i){            //从第2行开始
        for(int j=0;j<(1<<N);++j){
            if(((j&F[i-1])==j)&&check[j]){ //检查上一行，并枚举状态
                for(int k=0;k<(1<<N);++k){//枚举当前行的状态
                    if(((k&F[i])==k)&&!(j&k)&&check[k]) f[i][k]=(f[i][k]+f[i-1][j])%p;//当前行的数量+上一行在j状态下的数量
                }
            }
        }
    }
    for(int i=0;i<(1<<N);++i) ans=(ans+f[M][i])%p;//直接加最后一行，枚举所有的状态
    printf("%d\n",ans);
}