对于任意数制$R$的数$n$，都可以表达为$$n=\sum _{i=0}^k{a}_i{R}^i=a_0{R}^0+a_1{R}^1+a_2{R}^2+...+a_k{R}^k$$

一、十进制转$R$进制

方法：十进制数除$R$取余，余数倒着写
例：
66(D)→1000 010(B)计算过程：
①66/2=33，余数为0
②33/2=16，余数为1
③16/2=8，余数为0
④8/2=4，余数为0
⑤4/2=2，余数为0
⑥2/2=1，余数为0
⑦1/2=0，余数为1

66(D)→42(H)计算过程：
①66/16=4，余数为2
②4/16=0，余数为4

二、十六进制转二进制

方法：十六进制每一位写成四位的二进制数
例：42(H)→0100 0010(B)

三、八进制转二进制

方法：八进制每一位写成三位的二进制数
例：456(O)→100 101 110(B)

四、二进制转十进制

方法：二进制每一位加权求和
例：100 0010(B)→66(D)
计算过程：$$1\times 2^6+0\times 2^5+0\times 2^4+0\times 2^3+0\times 2^2+1\times 2^1+0\times 2^0=66$$

五、Java自带的进制处理

String s = Integer.toString(255, 16);//10进制数转0~35进制，结果为字符串
System.out.println("s="+s);

System.out.println(Integer.toString(666, 36));//666(D)转换为36进制

int a = Integer.parseInt(s, 16);//把字符串当做多少进制，结果转换为10进制
System.out.println("a="+a);

BigInteger m = new BigInteger(s,16);//把16进制的字符串封装为大数对象
System.out.println("big integer m="+m);

六、相关例题

1.题目介绍：
小赵对进制特别感兴趣，不必研究2进制, 3进制, 4进制, 5进制… ，突然有一次，他发现了一个特殊的数2992，这个数，它的十进制数表示，其四位数字之和为2+9+9+2=22，它的十六进制数BB0，其四位数字之和也为22，同时它的十二进制数表示1894，其四位数字之和也为22，啊哈，真是巧啊。之后他就去翻书，发现这种数叫sky数。但是要判|断这样的数还是有点麻烦啊，那么现在请你帮忙来判断任何一个十进制的四位数，是不是Sky数吧。

输入
输入含有些小10000000 整数，如果为0，则输入结束。

输出

若为Sky数，则输出“#n is a Sky Number."，否则输出“#n is not a Sky Number."每个结果占一行。注意：#n表示所读入的n值。

样例输入

1
2992
1234
0

样例输出

1 is a Sky Number.
2992 is a Sky Number.
1234 is not a Sky Number.
0 is a Sky Number.

思路分析：
sky数的十进制、十六进制、十二进制的数位和都相等

获得数n的不同数制R的数位和算法：

int getswh(int n, int R){
	int sum = 0;//存储R进制下的数位和
	while(n>0){
		sum = sum + n%R;
		n = n/R;
	}
	return sum;
}

程序代码：

import java.util.Scanner;

public class Test {

	public static void main(String[] args) {
		int a = 0;
		Scanner sc = new Scanner(System.in);
		while(sc.hasNext()) {
			a = sc.nextInt();
			if(getRsum(a, 10)==getRsum(a, 16) && getRsum(a, 10)==getRsum(a, 12))
				System.out.println(a + " is a Sky Number.");
			else
				System.out.println(a + " is not a Sky Number.");
		}
	}
	
	public static int getRsum(int n, int R){
		int sum = 0;//存储R进制下的数位和
		while(n > 0){
			sum = sum + n%R;
			n = n/R;
		}
		return sum;
	}
}

2.题目介绍：
求集合的所有子集。子集的个数为$2^k$，k表示集合的元素个数。
思路分析：

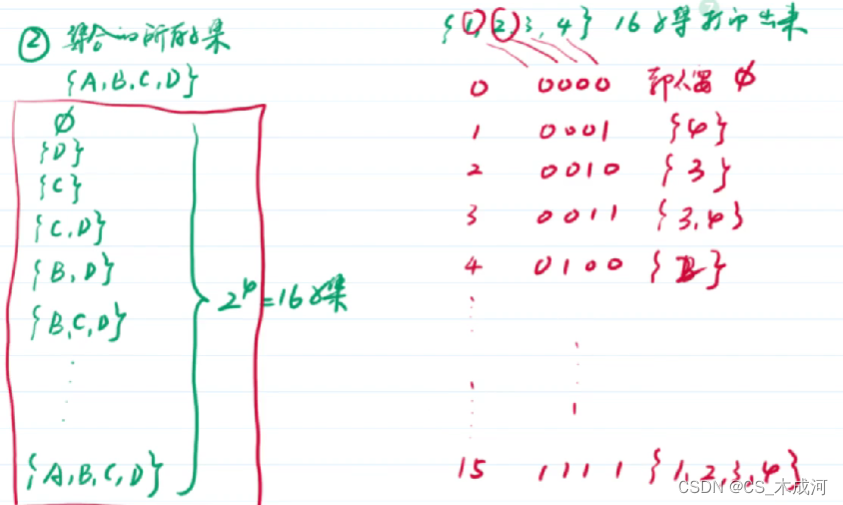
程序代码：

public class Test {

	public static void main(String[] args) {
		int[] a = {1, 2, 3, 4};
		for(int i=0;i<=15;i++) {
			System.out.print("{");
			int n = i;//存储当前要去转换成二进制的i
			int index = 0;//当前是第几次去除以2
			while(n>0) {
				if(n%2==1) {
					if(n>2)
						System.out.print(a[index]+" ");
					else
						System.out.print(a[index]);
				}
				index++;
				n = n/2;//不断缩小为原来的1/2
			}
			System.out.println("}");
		}
	}
}