代码随想录–栈与队列章节总结
1.LeetCode232 用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
- void push(int x) 将元素 x 推到队列的末尾
- int pop() 从队列的开头移除并返回元素
- int peek() 返回队列开头的元素
- boolean empty() 如果队列为空,返回 true ;否则,返回 false
说明:
你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
解题思路:栈的操作是先进后出的,队的先进先出。通过两个栈,正好可以把入栈顺序反转,实现队列的先进先出。利用两个栈即可实现队列操作
- 入队:将元素直接入栈到s1
- 出队:因为出队的顺序和出栈的顺序正好相反,因此需要另一个栈s2把顺序反转一下。出栈时如果s2中没有元素,则需要将s1中所有元素入栈到s2中。然后在从s2出栈一个元素
- peek:和出队操作一样,只不过这一次时直接返回s2栈顶元素的值,而不进行出栈
- 判断队列是否为空:只要s1和s2有一个不为空,则队列都不为空。
class MyQueue {
private Stack<Integer> stack1;
private Stack<Integer> stack2;
public MyQueue() {
stack1 = new Stack<>();
stack2 = new Stack<>();
}
public void push(int x) {
// 将元素保存到s1
stack1.push(x);
}
public int pop() {
// 判断s2是否为空,如果为空,则将s1中元素依次入栈到s2中
if (stack2.isEmpty()) {
while (!stack1.isEmpty()) stack2.push(stack1.pop());
}
// s2出栈
return stack2.pop();
}
public int peek() {
// 判断s2是否为空,如果为空,则将s1中元素依次入栈到s2中
if (stack2.isEmpty()) {
while (!stack1.isEmpty()) stack2.push(stack1.pop());
}
// s2出栈
return stack2.peek();
}
public boolean empty() {
return stack1.isEmpty() && stack2.isEmpty();
}
}
2.LeetCode225 使用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
- void push(int x) 将元素 x 压入栈顶。
- int pop() 移除并返回栈顶元素
- int top() 返回栈顶元素
- boolean empty() 如果栈是空的,返回 true ;否则,返回 false 。
注意:
你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
解题思路1: 使用两个队列实现。
- 入栈:直接将元素入队列到q1
- 出栈:把q1中的size-1个元素都保存到q2中,然后q1出队队后一个元素
- 栈顶:q1中最后一个元素就是栈顶元素
- 判空:两个队列都为空的时候,则栈为空
class MyStack {
Deque<Integer> queue1;
Deque<Integer> queue2;
public MyStack() {
queue1 = new ArrayDeque<>();
queue2 = new ArrayDeque<>();
}
public void push(int x) {
queue1.offer(x);
}
public int pop() {
// 将队列1中的size-1个元素出队,存入队列2中
// 这个地方这个size一定要在循环外面获取
int size = queue1.size();
// queue1.size() - 1 这样写不对,因为循环一次queue1.size()就会变化
// for (int i = 0; i < queue1.size() - 1; i++) {
for (int i = 0; i < size - 1; i++) {
queue2.offer(queue1.poll());
}
Deque<Integer> temp = queue1;
queue1 = queue2;
queue2 = temp;
return queue2.poll();
}
public int top() {
return queue1.peekLast();
}
public boolean empty() {
return queue1.isEmpty() && queue2.isEmpty();
}
}
这个地方使用了Deque而不是Queue,主要原因是因为Queue无法使用peekLast()函数,无法获取一个队列的队尾元素。
图解:

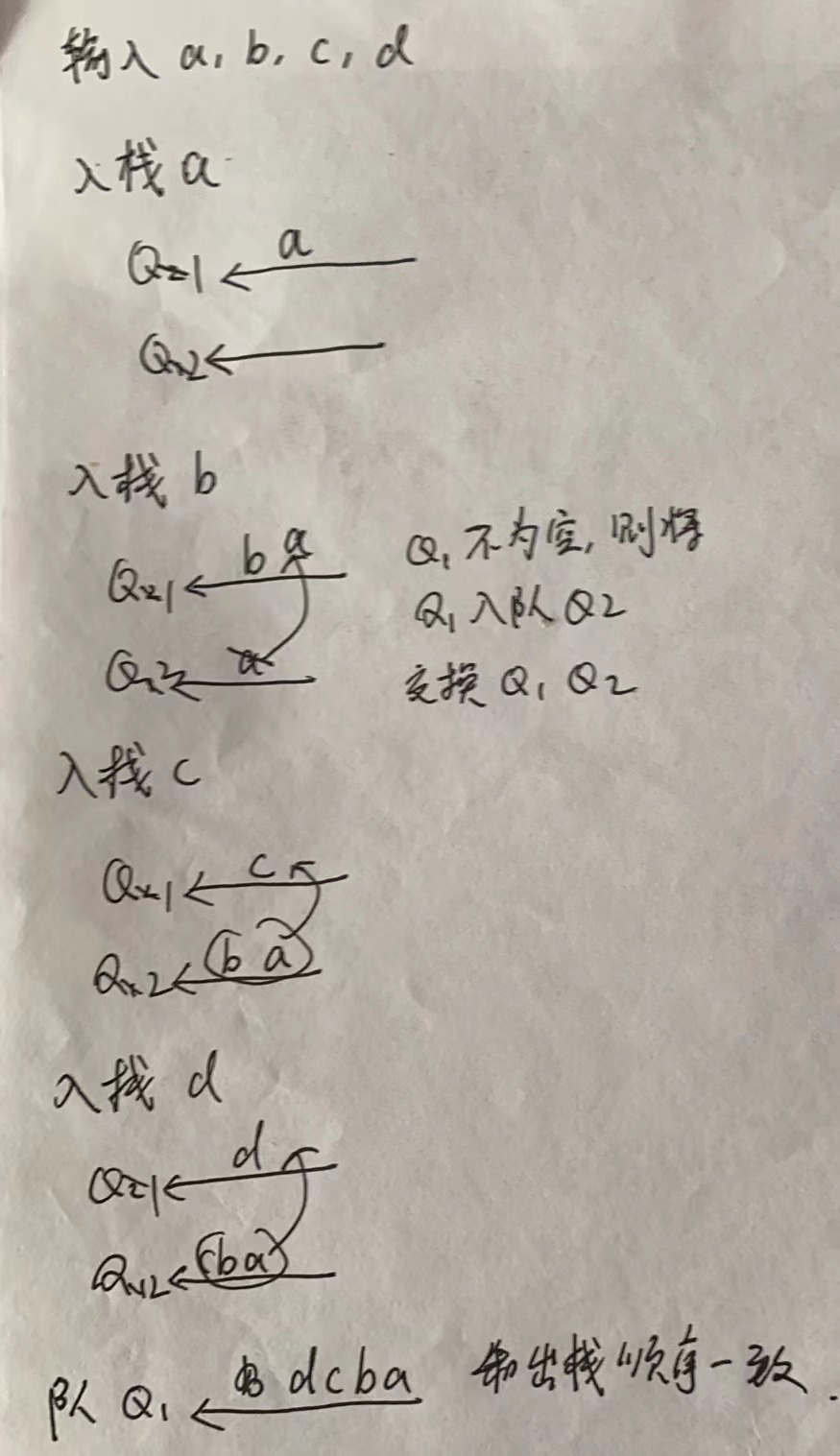
解题思路2:同样利用双队列
- 入栈:首先将元素入队到q2,然后判断q1中是否有元素,如果有元素,将q1中元素都入队到q2。然后交换q1和q2
- 出队:直接从q1出队
- 栈顶:q1队首就是栈顶
这个的思路是始终让q1中元素顺序和出栈顺序保持一致
class MyStack {
Queue<Integer> queue1;
Queue<Integer> queue2;
public MyStack() {
queue1 = new LinkedList<>();
queue2 = new LinkedList<>();
}
public void push(int x) {
// 始终让q1中元素顺序和栈中顺序一致
// 插入元素,先放到q2中
queue2.offer(x);
// 判断q1中是否有元素,如果有,则把q1中的元素都移动的q2中
while (!queue1.isEmpty()) queue2.offer(queue1.poll());
// 交换q1和q2
Queue<Integer> temp = queue1;
queue1 = queue2;
queue2 = temp;
}
public int pop() {
return queue1.poll();
}
public int top() {
return queue1.peek();
}
public boolean empty() {
return queue1.isEmpty() && queue2.isEmpty();
}
}
图解:
解题思路3:使用一个队列。
- 入栈:正常入队
- 出栈:将队列中前size-1个元素都出队,然后依次插入到队尾中。结束以后,队首元素就是要出栈的元素
- peek:队中最后一个元素
class MyStack {
Deque<Integer> queue;
public MyStack() {
queue = new ArrayDeque<>();
}
public void push(int x) {
queue.push(x);
}
public int pop() {
int size = queue.size();
size--;
// 将 que1 导入 que2 ,但留下最后一个值
while (size-- > 0) {
queue.addLast(queue.peekFirst());
queue.pollFirst();
}
int res = queue.pollFirst();
return res;
}
public int top() {
return queue.peekLast();
}
public boolean empty() {
return queue.isEmpty();
}
}
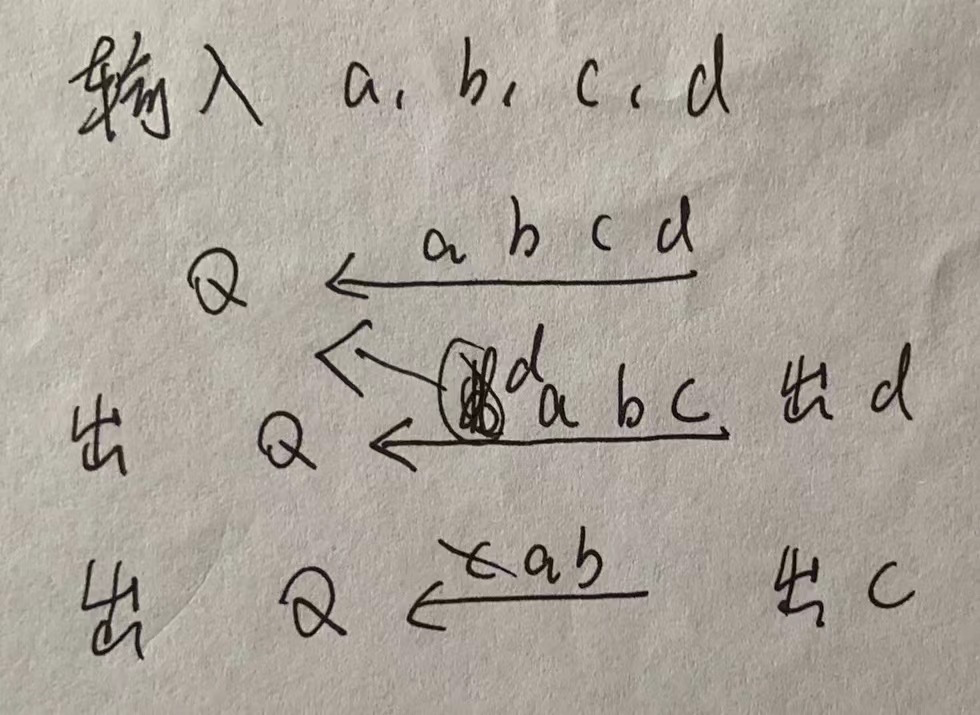
3.Leetcode20 有效的括号
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
解题思路:使用栈
- 如果字符串长度小于2,那么直接返回false
- 只要碰到( [ { 就入栈,碰到其他的就匹配出栈
- 在else中需要先判断一下栈是否为空,如果为空,则直接返回false
- 遍历完整个字符串后,需要判断栈是否为空,如果不为空,则匹配失败。
public boolean isValid(String s) {
// 如果字符串长度为1,则直接返回false
if (s.length() <= 1) return false;
// 创建一个栈
Stack<Character> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c == '(' || c == '{' || c == '[') {
// 入栈
stack.push(c);
} else {
// 如果栈为空,也就是截止到目前都匹配上了,这时候如果出现)},则一定匹配出错
// 举个例子输入字符串是")}"
if (stack.isEmpty()) return false;
// 将取出的元素c和栈顶元素进行比较,如果相等,则栈顶元素出栈
// 如果不相等,则返回false
if (c == ')' && stack.peek() == '(')
stack.pop();
else if (c == ']' && stack.peek() == '[')
stack.pop();
else if (c == '}' && stack.peek() == '{')
stack.pop();
else
return false;
}
}
// 最后需要判断栈是否为空,如果不为空,则匹配失败
// 举个例子"(("
return stack.isEmpty();
}
图解:
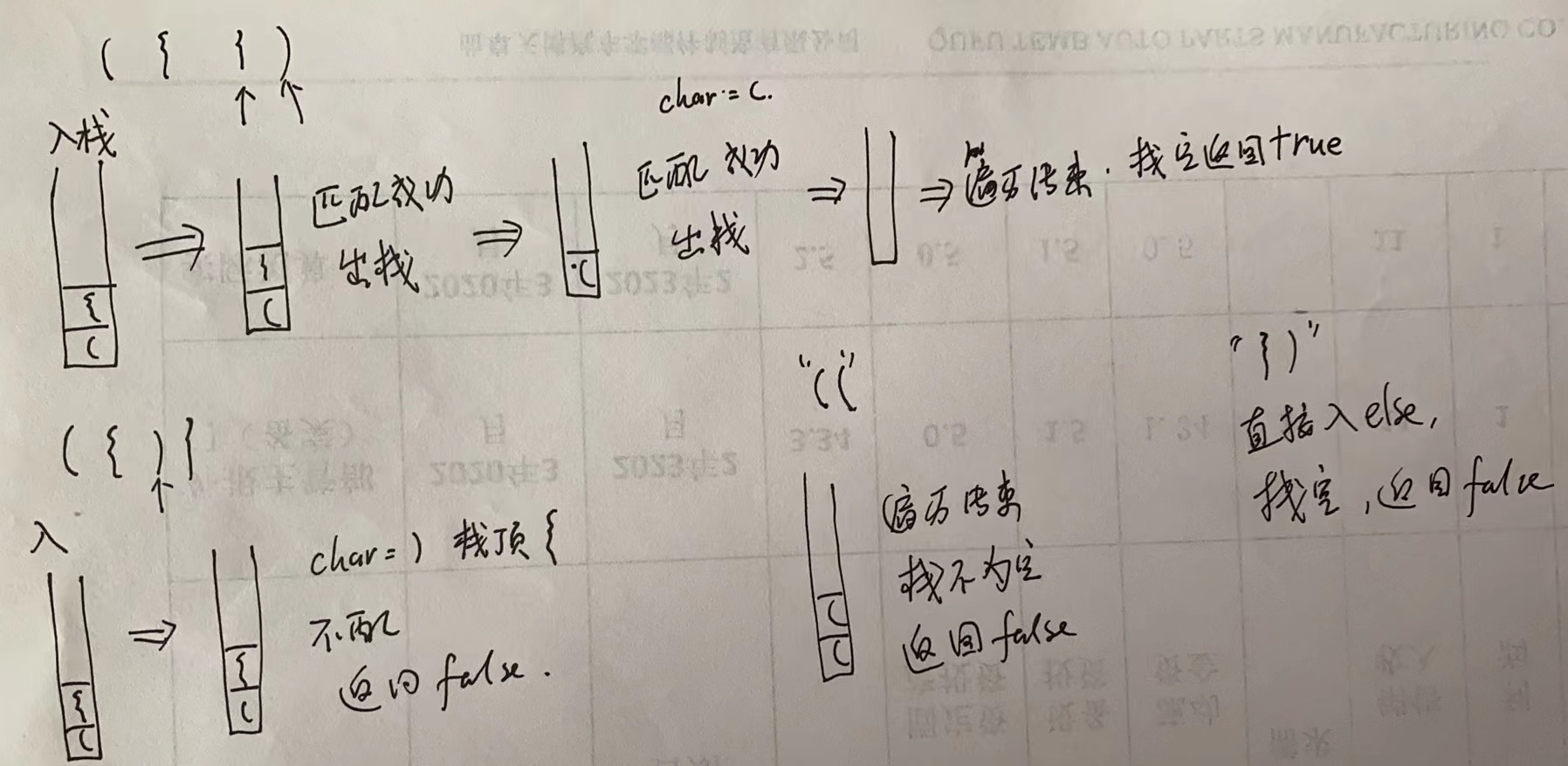
4.Leetcode1027 删除字符串中的所有相邻重复项
给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。
在 S 上反复执行重复项删除操作,直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
示例:
输入:"abbaca"
输出:"ca"
解释:
例如,在 "abbaca" 中,我们可以删除 "bb" 由于两字母相邻且相同,这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca",其中又只有 "aa" 可以执行重复项删除操作,所以最后的字符串为 "ca"。
解题思路: 这个题可以使用栈来解决。
- 首先判断字符串长度,如果小于2,则直接返回
- 创建一个栈,让字符串的第一元素入栈。
- 然后遍历字符串中的每一个元素,和栈顶元素做比较,如果相等,则栈顶元素出栈。如果栈为空或者栈顶元素不相等,则让当前遍历的元素入栈
- 直到整个字符串被遍历完毕后。使用StringBuilder构建字符串即可。
public static String removeDuplicates(String s) {
// 如果字符串长度小于2,直接返回即可
if (s.length() < 2) return s;
// 创建一个栈
Stack<Character> stack = new Stack<>();
// 第一个元素直接入栈
stack.push(s.charAt(0));
for (int i = 1; i < s.length(); i++) {
// 如果栈顶元素和取出来的元素不相等,或者栈为空,则将元素入栈
if (stack.isEmpty() || stack.peek() != s.charAt(i))
stack.push(s.charAt(i));
else
// 如果相等,则出栈
stack.pop();
}
// 栈中所有元素出栈
StringBuilder stringBuilder = new StringBuilder();
while (!stack.isEmpty()) {
stringBuilder.append(stack.pop());
}
return stringBuilder.reverse().toString();
}
图解:
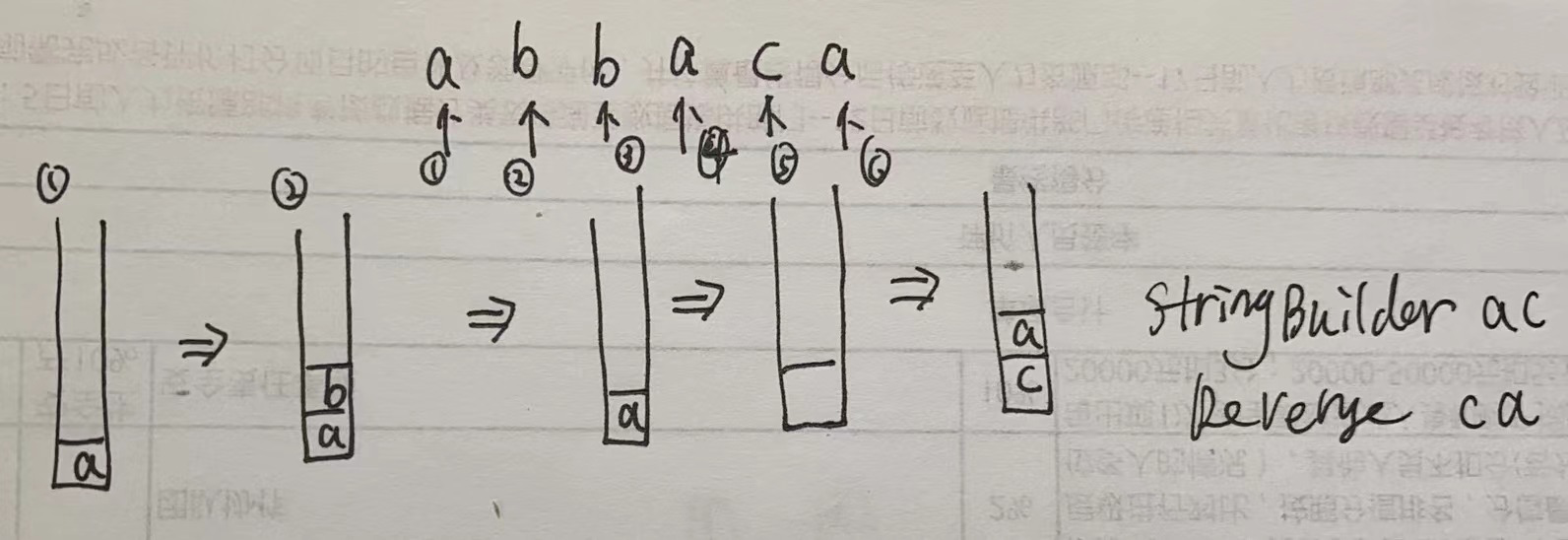
5.Leetcode105 逆波兰式的求解
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
有效的算符为 ‘+’、‘-’、‘*’ 和 ‘/’ 。
每个操作数(运算对象)都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。
示例 1:
输入:tokens = ["2","1","+","3","*"]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = ["4","13","5","/","+"]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
解题思路: 利用栈来解决。
- 首先判断给出的数组的长度是不是小于等于2,如果是,则报错。因为操作至少需要两个操作数和一个操作符才行。
- 将数组中的前两个元素入栈。前两个元素一定是数字。
- 开始遍历字符串数组,每遍历一个就判断一下是否是运算符,如果是,则将栈中出栈两个元素,并按照运算符进行运算,并且将结果入栈
- 如果不是运算符,则直接将元素入栈
- 遍历完成后,栈中的唯一一个元素就是逆波兰式的结果。
public int evalRPN(String[] tokens) {
if (tokens.length <= 2) return Integer.parseInt(tokens[0]);
// 创建一个栈
Stack<Integer> stack = new Stack<>();
// 前两个元素入栈
stack.push(Integer.parseInt(tokens[0]));
stack.push(Integer.parseInt(tokens[1]));
// 开始遍历
for (int i = 2; i < tokens.length; i++) {
String token = tokens[i];
// 判断token是运算符么
if (isOperation(token)) {
// 先出栈两个操作数
Integer b = stack.pop();
Integer a = stack.pop();
Integer res = null;
switch (token) {
case "+" :
res = a + b;
break;
case "-" :
res = a - b;
break;
case "*":
res = a * b;
break;
case "/" :
res = a / b;
break;
}
// 将结果入栈
stack.push(res);
}
else {
// 不是运算符那么直接入栈
stack.push(Integer.parseInt(token));
}
}
return stack.pop();
}
private boolean isOperation(String token) {
if (token.equals("*") || token.equals("+") || token.equals("-") || token.equals("/"))
return true;
return false;
}
这里需要注意的一点是如果表示式为[“6”,“3”,“/”],他对应的计算应该是6/3还是3/6
在这个题中,给出了栗子,应该是6/3

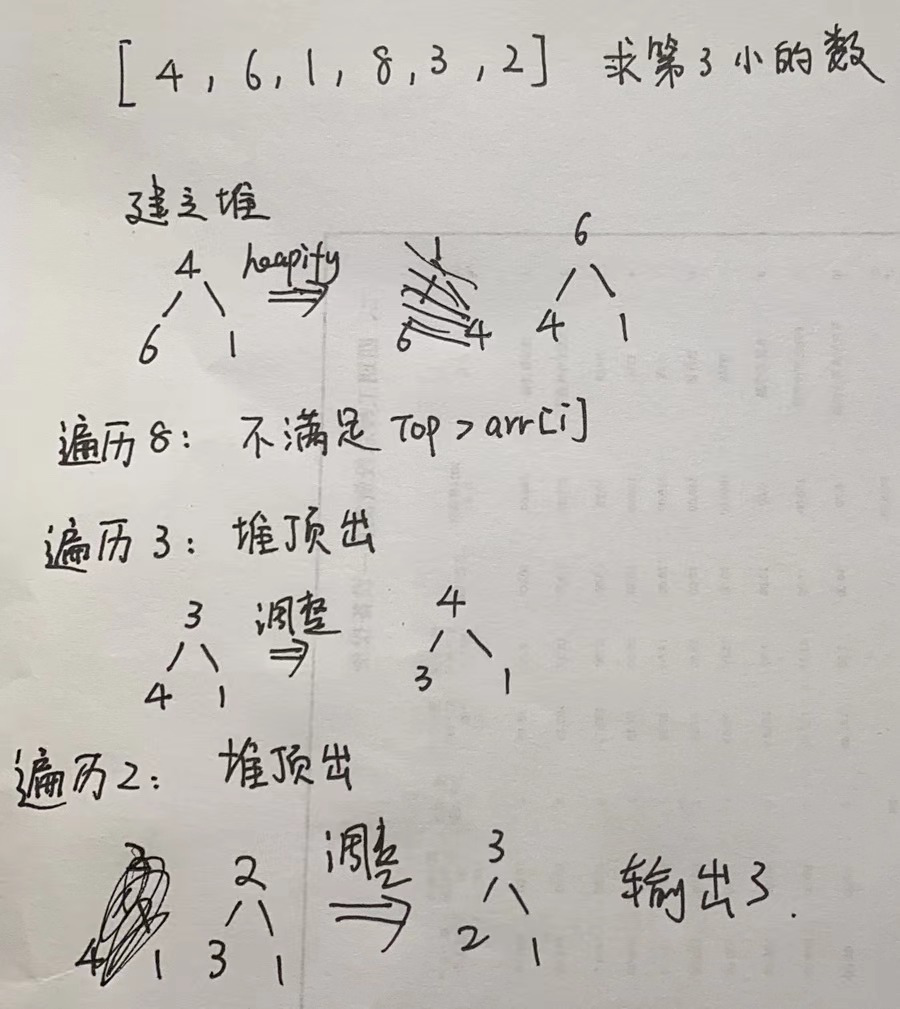
6.求TopK的数
给定一个很大的数组,长度100w,求第k大的数是多少?
这个问题是一个很经典的问题,如果采用传统方式,即现排序,然后找到第k个数,对于数据量很大的时候,是非常耗时的。对于这个问题,最好的解决方案是使用堆排序。
- 具体来说,首先取数组中前k个字符,保存到堆中,顺序堆会自动调整。
- 然后从k+1开始遍历数组,每次都和堆顶元素进行比较。如果我们要求第k大的数,那么需要建立小顶堆。那么遍历的元素如果比堆顶元素小,那么堆顶弹出,把遍历元素放入堆中。
- 完全遍历之后,堆顶元素就是第k大的元素。
求第k个大的数,需要建立小顶堆。小顶堆的意思是堆顶元素最小,那么在这个有k个元素的堆中,k-1个元素都比堆顶元素大,那么堆顶元素不就是第k大的了么。
同理如果求第k小的数,需要建立大顶堆。在堆中,k-1个元素都比堆顶元素小,那么堆顶元素就是第k小的元素。
在Java中,我们使用优先队列来实现上述操作,因为优先队列的底层实现就是堆。
// 求第k小的数
private static int heap(int[] arr, int k) {
// 创建一个大小为k的,大顶堆
PriorityQueue<Integer> queue = new PriorityQueue<>(k, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});
// 循环整个数组,让前k个元素直接存入大顶堆中,从第k+1个元素开始需要和堆顶进行比较
for (int i = 0; i < arr.length; i++) {
if (queue.size() < k) {
queue.offer(arr[i]);
} else {
int top = queue.peek();
if (top > arr[i]) {
queue.poll();
queue.offer(arr[i]);
}
}
}
return queue.poll();
}
这里我们需要注意的是,优先队列默认的是小顶堆,如果我们要创建大顶堆,需要重写比较器。
下面进行了对比实验,对比了直接排序法和使用堆排序的耗时
public static void main(String[] args) {
int k = 25;
int[] arr = new int[200000000];
Random random = new Random();
for (int i = arr.length - 1, j = 0; i >= 0; i--) {
arr[i] = random.nextInt();
}
Long start = System.currentTimeMillis();
int sort = sort(arr, k); // 直接排序
Long end = System.currentTimeMillis();
System.out.print("使用普通排序耗时:");
System.out.println(end - start);
System.out.println(sort);
Long start1 = System.currentTimeMillis();
int heap = heap(arr, k);
Long end1 = System.currentTimeMillis();
System.out.print("使用heap排序耗时:");
System.out.println(end1 - start1);
System.out.println(heap);
}
private static int sort(int[] arr, int k) {
Arrays.sort(arr);
return arr[k - 1];
}
使用普通排序耗时:24185ms
第k小的数为:-2147482892
使用heap排序耗时:528ms
第k小的数为:-2147482892
从结果可以看出来差距还是和明显的
这里需要注意判断是否需要出堆顶元素的条件
- 对于大顶堆来说 top > arr[i]
- 对于小顶堆来说 top < arr[i]
下面举一个例子,求第三小的数,图解如下:




![[C语言]柔性数组](https://img-blog.csdnimg.cn/58124fa67317420a88e80898b086f615.png)