文章目录
- 引入
- 树状数组
- c++完整代码
引入
什么是树状数组???
解决数据压缩里的累积频率(Cumulative Frequency)的计算问题,现多用于高效计算数列的前缀和, 区间和,这样的问题可以使用树状数组算法来解决。
- 前面我们讲过求静态数组的子区间和,我们可以利用前缀和来求得。
- 而现在我们引入动态数组的子区间和这一问题,我们可以使用树状数组。
我们现在通过修改数组,往数组中某一个位置增加或减小一个值,从而导致前缀和数组会发生变化,因此我们不可以使用普通前缀和这一思路来做。
考虑一下:我们求静态数组的前缀和时,如果我们使用暴力法,使用两个for循环来枚举子区间之和,从而得到静态数组的区间和,但是这一复杂度会达到O(N^2),因此使用普通的前缀和可以将复杂度达到O(N)。但是当我们在动态数组中修改元素时,每次修改元素会导致原来的前缀和发生变化,因此我们还需要维护前缀和,这样的时间复杂度也会达到O( N^2)。
但是如果我们使用树状数组这一算法,时间复杂度将会降为O(nlog2n),接下来我将详细解释一下树状数组
树状数组
树状数组包含三个基本的功能:
- 维护前缀和数组:在某个位置增加减少值时,需要调用此函数,来动态维护前缀和
- 查询前缀和:求某个区间 [l,r]的区间和,即 sum[r]-sum[l-1]
- lowbit运算:这个概念非常重要,用于得到某个数的二进制的最低位的一,有什么用呢,我们待会再说。
首先定义tree数组表示一个树状数组 ,tree[i]表示第i个位置的区间的和,区间[l,r]的和即为tree[r]-tree[l-1]
- 首先来看维护前缀和数组:update的函数意思是在数组的 第i个元素加上元素x,x可以是正负,分别代表tree[i]加或者减一个值
//维护
void update(int i,int x)
{
/*
i:下标
x:增量
维护:在末尾的1上加1
*/
while (i <= n)
{
tree[i] += x;
i += lowbit(i);
}
}
- 查询区间的和: 求[l,r]的区间和即为 sum[r]-sum[l-1]
//求和
int sum(int i)
{
/*
求和(查询):去除末尾的1
*/
int num = 0;
while (i)
{
num += tree[i];
i -= lowbit(i);
}
return num;
}
- lowbit操作:当前一个数字的补码与原数相与得到的便是当前数字二进制的最后一个1。
inline int lowbit(int x)
{
return ((x) & (-x));
}
接下来详细解释一个这三个函数基本功能:
引用《百度百科》的一张图来解释
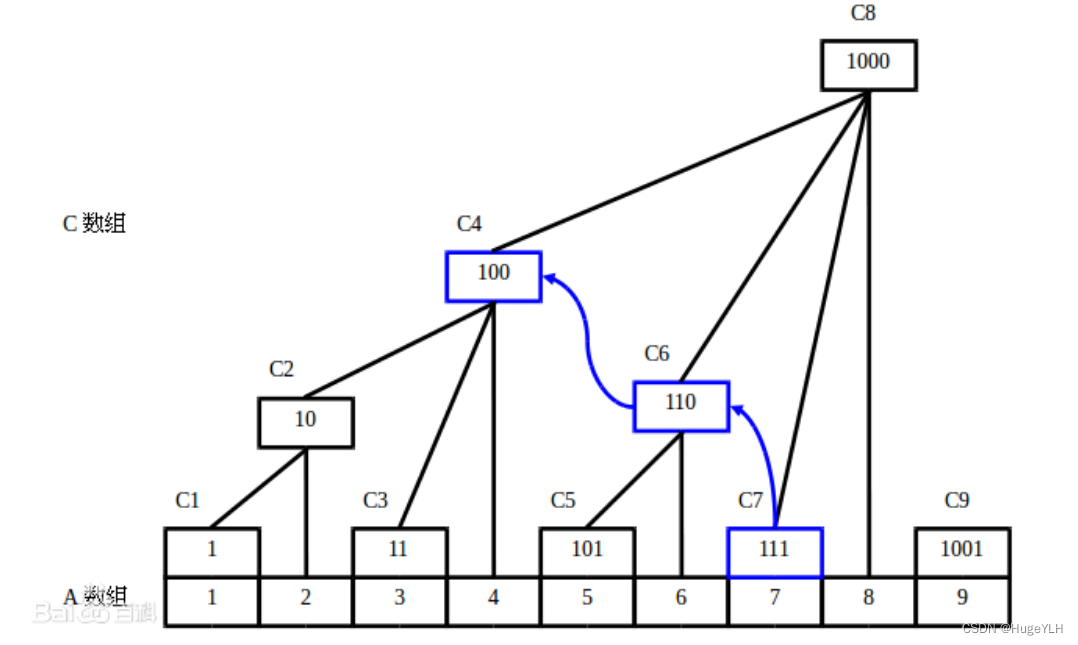
对于查询的过程:每次去掉二进制的最后的1,例如我们查询sum(7):
- 7的二进制是 111 ,去掉最后的1,得到:110,即十进制为6,则sum(6)
- 6的二进制是110,去掉最后的1,得到:100,即十进制为4,则sum(4)
- 4的二进制是100,去掉最后的1,得到:0,为零则结束
所以说查询sum(7)就等于:sum(7) = sum(6)+sum(4),如上图的蓝色表示。
对于维护的过程:每次在二进制数最后的1上加1,例如我们更新update(1,2):
- 1的二进制是1,在最后一个1上加1得10,十进制为2,所以说tree[2]也会跟着修改
- 2得二进制是10,在最后一个1上加1得100,十进制为4,所以说tree[4]也会跟着修改
- 4得二进制是100,在最后一个1上加1得1000,十进制为8,所以说tree[8也会跟着修改
所以说当维护(修改一个位置的元素值)时,我们会自动动态的维护整个树状数组,修改tree[1]+=2 ,tree[2] tree[4] tree[8] … 都会跟着修改。,一直到整个数组的大小N为止。
对于lowbit运算的过程:
lowbit运算可以得到二进制最后一个1的位置,同时也可以根据lowbit确定tree数组的构成
首先我们需要理解tree数组的意思:tree数组本质是前缀和,即tree[i]=a[1]+a[2]+…+a[i]的区间的和。
接下来我们枚举1-7数字的二进制以及lowbit运算的结果,看看lowbit运算是如何影响tree数组的

首先我们可以了解到:
- 数字i为奇数时,lowbit始终结果为1,因此我们就可以推断这个1代表tree[i]=a[i] ,代表它只有一个原数组a[i]的值
- 数字i为偶数时,lowbit结果似乎从数字2,4来看满足:2的时候有两项,4的时候有四项吗,但是并不是这样!!!!!!比如数字6就只有2项。当i为偶数的时候,实际上看的是二进制的最后一位数字1及其之后所表示的低位的值,例如 10就是2;100就是4,110就是2(10);11110还是2(最后一位1与后面的0);11000就是8
因此:tree数组的每一项的值:
- 当数字为1时,lowbit运算为1,所以tree[1]=a[1] (奇数肯定只有一项)
- 当数字为2时,lowbit运算为10,所以tree[2]=a[2]+a[1],有两项
- 当数字为3时,lowbit运算为1,所以tree[3]=a[3]
- 当数字为4时,lowbit运算为100,所以tree[4]=a[4]+a[3]+a[2]+a[1] ,有四项
- 当数字为5时,lowbit运算为1,所以tree[5]=a[5]
- 当数字为6时,lowbit运算为10,所以tree[6]=a[6]+a[5] ,有两项
- 当数字为7时,lowbit运算为1,所以tree[7]=a[7]
- 当数字为8时,lowbit运算为1000,所以tree[8]=a[8]+ … a[1],有八项
即我们可以得到这样一张图:
请仔细理解这张图代表的意义!!!!!!!!!
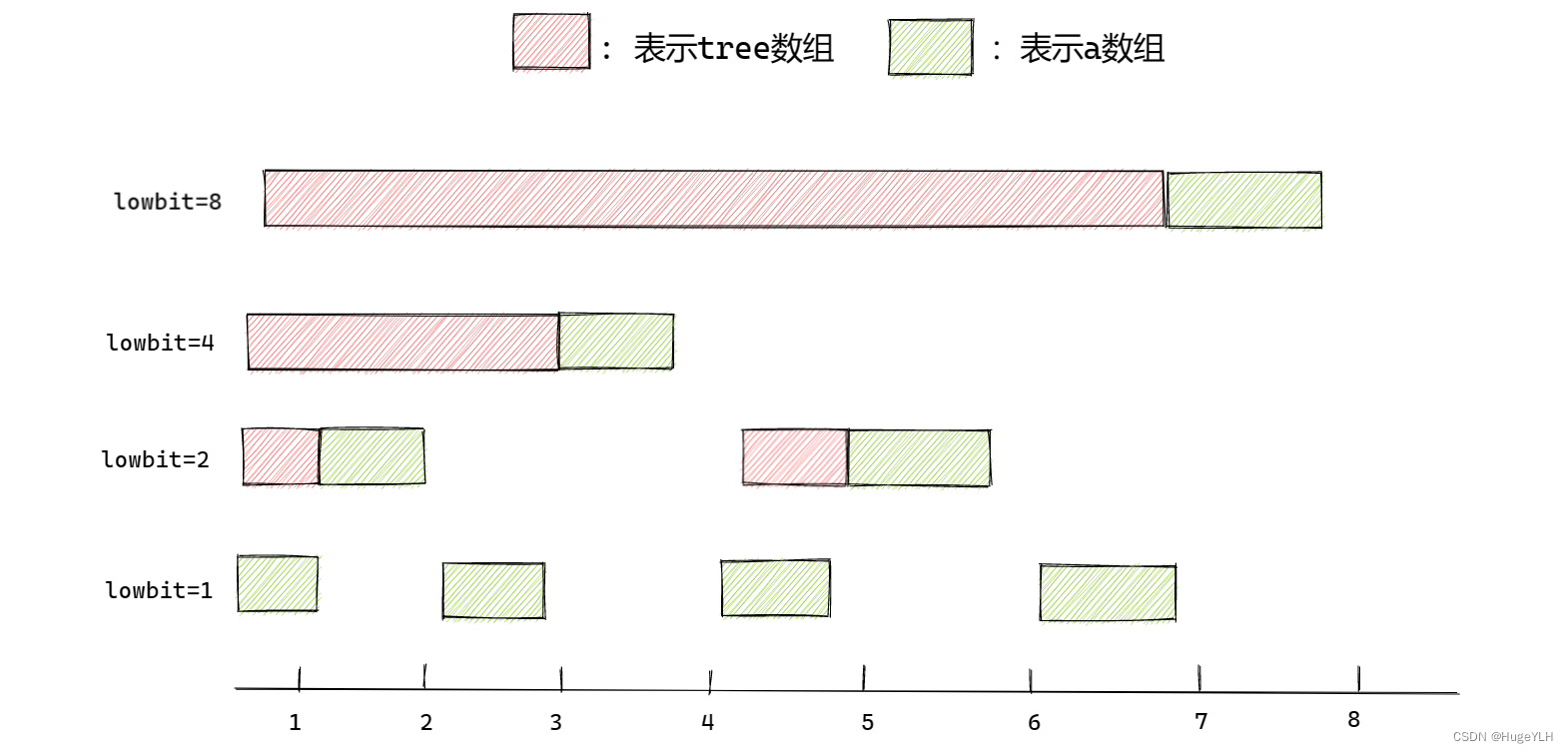
对于tree[4]=a[1]+a[2]+a[3]+a[4],其实就是tree[4]=tree[3]+a[4],对于其他也是同理。
c++完整代码
#include <bits/stdc++.h>
using namespace std;
/*
树状数组:常用于对动态区间的查询操作,即求动态数组求前缀和的操作
三大基本功能:
1. 维护 update
2. 求和 sum
3. lowbit运算
*/
const int N = 10005;
int tree[N]{ 0 };
int n; //当前tree数组的最大元素个数
inline int lowbit(int x)
{
return ((x) & (-x));
}
//维护
void update(int i,int x)
{
/*
i:下标
x:增量
维护:在末尾的1上加1
*/
while (i <= n)
{
tree[i] += x;
i += lowbit(i);
}
}
//求和
int sum(int i)
{
/*
求和(查询):去除末尾的1
*/
int num = 0;
while (i)
{
num += tree[i];
i -= lowbit(i);
}
return num;
}
int main()
{
n = 5;
for (int i = 1; i <= 5; i++)
{
update(i, 3);
}
// 3 6 9 12 15
cout << "S[2,4]: " << sum(4) - sum(1) << endl;
//更新数组元素
// 3 6 15 18 21
update(3, 6);
cout << "S[2,4]: " << sum(4) - sum(1) << endl;
return 0;
}