在Java中使用堆排序求解TopK问题

1. 问题描述

给定一个很大的数组，长度100w，求第k大的数是多少？

这个问题是一个很经典的问题，如果采用传统方式，即现排序，然后找到第k个数，对于数据量很大的时候，是非常耗时的。对于这个问题，最好的解决方案是使用堆排序。

2. 暴力解法

最容易想到的办法就是暴力方法，直接将这个数组进行排序，然后直接输出第k-1位置上的元素即可。这种方法对于数据量小的时候，是最简单并且使用的方法，但是设想一下，当数据量高达千万一别的时候，对这些数据排序所话费的时间是很恐怖的。

3. 使用堆解决

我们在学习数据结构的时候学习过，堆在求解第TopK问题的时候是非常高效的，因为他不需要对所有的数据都进行排序，具体的方法如下：

• 具体来说，首先取数组中前k个字符，保存到堆中，顺序堆会自动调整。
• 然后从k+1开始遍历数组，每次都和堆顶元素进行比较。如果我们要求第k大的数，那么需要建立小顶堆。那么遍历的元素如果比堆顶元素小，那么堆顶弹出，把遍历元素放入堆中。
• 完全遍历之后，堆顶元素就是第k大的元素。

求第k个大的数，需要建立小顶堆。小顶堆的意思是堆顶元素最小，那么在这个有k个元素的堆中，k-1个元素都比堆顶元素大，那么堆顶元素不就是第k大的了么。

同理如果求第k小的数，需要建立大顶堆。在堆中，k-1个元素都比堆顶元素小，那么堆顶元素就是第k小的元素。

在Java中，我们使用优先队列来实现上述操作，因为优先队列的底层实现就是堆。

// 求第k小的数
private static int heap(int[] arr, int k) {
    // 创建一个大小为k的，大顶堆
    PriorityQueue<Integer> queue = new PriorityQueue<>(k, new Comparator<Integer>() {
        @Override
        public int compare(Integer o1, Integer o2) {
            return o2 - o1;
        }
    });
    // 循环整个数组，让前k个元素直接存入大顶堆中，从第k+1个元素开始需要和堆顶进行比较
    for (int i = 0; i < arr.length; i++) {
        if (queue.size() < k) {
            queue.offer(arr[i]);
        } else {
            int top = queue.peek();
            if (top > arr[i]) {
                queue.poll();
                queue.offer(arr[i]);
            }
        }
    }
    return queue.poll();
}

这里我们需要注意的是，优先队列默认的是小顶堆，如果我们要创建大顶堆，需要重写比较器。

4. 对比直接排序方法和使用堆排序方法的耗时

下面进行了对比实验，对比了直接排序法和使用堆排序的耗时

public static void main(String[] args) {
      int k = 25;
      int[] arr = new int[200000000];
      Random random = new Random();
      for (int i = arr.length - 1, j = 0; i >= 0; i--) {
          arr[i] = random.nextInt();
      }
      Long start = System.currentTimeMillis();
      int sort = sort(arr, k); // 直接排序
      Long end = System.currentTimeMillis();
      System.out.print("使用普通排序耗时:");
      System.out.println(end - start);
      System.out.println(sort);

      Long start1 = System.currentTimeMillis();
      int heap = heap(arr, k);
      Long end1 = System.currentTimeMillis();
      System.out.print("使用heap排序耗时:");
      System.out.println(end1 - start1);
      System.out.println(heap);
  }

private static int sort(int[] arr, int k) {
    Arrays.sort(arr);
    return arr[k - 1];
}

使用普通排序耗时:24185ms
第k小的数为：-2147482892
使用heap排序耗时:528ms
第k小的数为：-2147482892

从结果可以看出来差距还是和明显的

这里需要注意判断是否需要出堆顶元素的条件

• 对于大顶堆来说 top > arr[i]
• 对于小顶堆来说 top < arr[i]

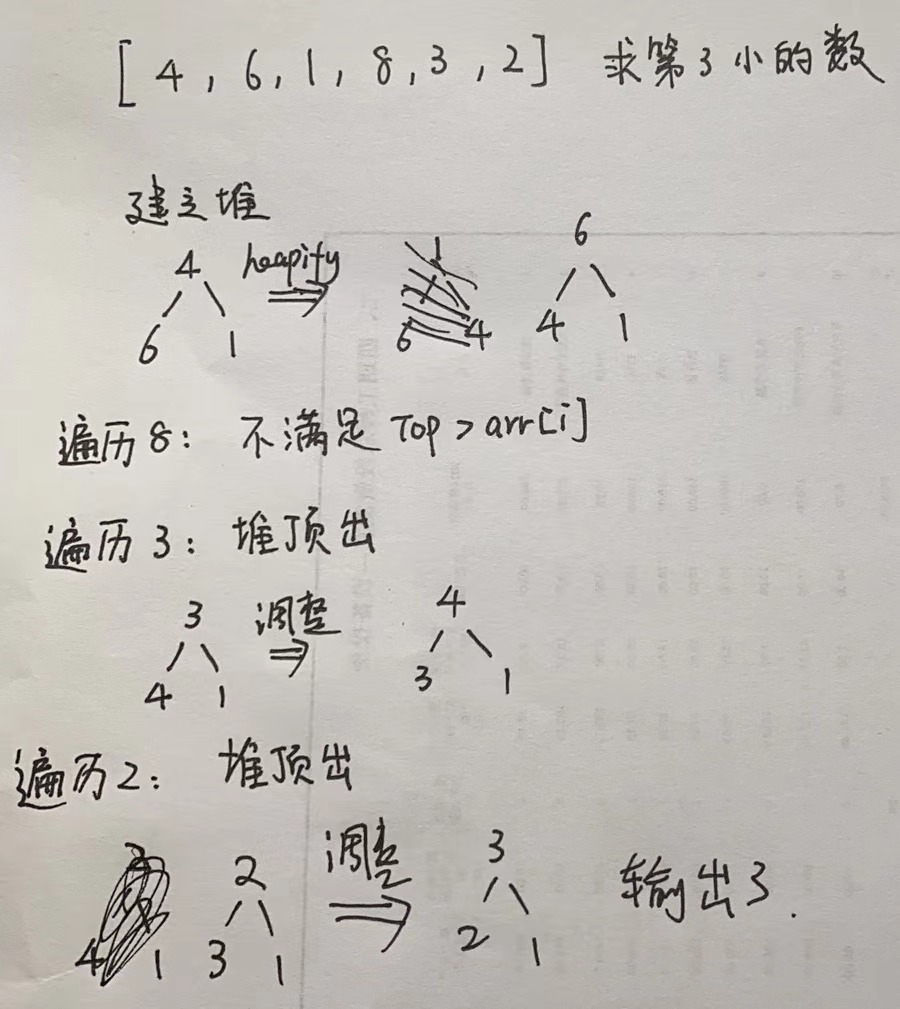
5. 图解举例说明具体过程

下面举一个例子，求第三小的数，图解如下：