1、快速幂
1.1运算模
定义:模运算为a除以m的余数,记为a mod m,有a mod m = a % m。
- 模运算是大数运算中的常用操作:如果一个数太大,无法直接输出,或者不需要直接输出,可以把它取模后,缩小数值再输出。
- Python虽然能直接计算大数,不用担心数据溢出,但是大数乘法太耗时,所以也常用取模来缩小数值。
- 一个简单应用,判断奇偶:a%2==0,a是偶数;a%2==1,a是奇数
例题一:刷题统计
2022年第十三届省赛,lanqi ao0J题号209
问题描述
小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天 做 a 道题目, 周六和周日每天做 b 道题目。请你帮小明计算, 按照计划他将在 第几天实现做题数大于等于 n 题?
输入格式
输入一行包含三个整数 a,b 和 n.
输出格式
输出一个整数代表天数。
样例输入
10 20 99样例输出
8
思路
求余数的简单题,利用求余,把计算复杂度降为0(1)。
a, b, n =map (int, input ().split ())
week = a*5+b*2 # 每周一共做题数
days = (n//week)*7 # 整周的做题天数(不满一周的不计)
n %= week # 最后一周做题数
if n <= a*5: # 最后一周在前五天完成
#Python的三目运算
days += n//a+(1 if n%a>0 else 0) # 总天数=整周天数+最后一周天数
else: # 最后一周在后两天完成
days += 5 # 把前五天先加上
n -= a*5 # 把最后一周后两天的做题数
days += n//b+(1 if n%b>0 else 0) # 加上最后一周后两天做题天数(先整除再取余)
print(days)1.2快速幂
- 幂运算
,当n很大时,如果一个个地乘,时间是O(n)的,速度很慢,此时可以用快速幂,在O(logn)的时间内算出来。
- 快速幂的一个解法:分治法,算
,然后再算
,..,一直算到
,代码也容易写。
- 标准的快速幂:用位运算实现。基于位运算的快速幂,原理是倍增。
1.3快速幂原理
以为例说明如何用倍增法做快速幂。
(1)幂次与二进制的关系。把分解成幂
的乘积:
。其
人中..的幂次都是2的倍数,所有的幂
都是倍乘关系,逐级递推,代码: a*=a
(2)幂次用二进制分解。如何把11分解为8+2+1?利用数的二进制的特征,,把n按二进制处理就可以。
(3)如何跳过那些没有的幂次?例如1011需要跳过。做个判断,用二进制的位运算实现:
- n & 1 取n的最后一位,并且判断这一位是否需要跳过
- n >>=1 把n右移一位,目的是把刚处理过的n的最后一位去掉。
- 直到全部移除(n=0)才退出
幂运算的结果往往很大,一般会先取模再输出。
根据取模的性质有:
例题二:快速幂(模板题)
lanqiao0J题号1514
题目描述
输入 b,p,k 的值,求
的值。其中 2≤b,p,k≤
。
输入描述
三个整数 b,p,k。
输出描述
输出
=s,s 为运算结果。
输入输出样例
输入
2 10 9输出
7
代码
def fastPow(a, n,mod):
ans = 1
while n: # 把n看成二进制,逐个处理它的最后一位
if n&1:
ans = ans * a % mod # 如果n的最后一位是1,表示这个地方需要乘
a = a*a % mod # 递推: a^2 --> a^4 --> a^8--> a^16...
n >>= 1 # n右移一位,把刚处理过的n的最后一位去掉
return ans
b, p,k = map(int,input ().split())
print(fastPow(b, p,k))第五六行代码是 取模的性质: ,先括号里面再外面
例题三:RSA解密
2019年第十届省赛,填空题,lanqiao0J题号603
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
RSA 是一种经典的加密算法。它的基本加密过程如下。
首先生成两个质数 p,q,令 n=p⋅q,设 d 与 (p−1)⋅(q−1) 互质,则可找到 e 使得 d⋅e 除 (p−1)⋅(q−1) 的余数为 11。
n,d,e 组成了私钥,n,d 组成了公钥。
当使用公钥加密一个整数 X 时(小于 n),计算 C=
mod n,则 C 是加密后的密文。
当收到密文 C 时,可使用私钥解开,计算公式为 X=
mod n。
例如,当 p=5,q=11,d=3 时,n=55,e=27。
若加密数字 24,得
mod 55=19。 解密数字 19,得
mod 55=24。
现在你知道公钥中 n=1001733993063167141,d=212353,同时你截获了别人发送的密文 C=20190324,请问,原文是多少?
题解
(1)求p、q (两个质数p、q,n=pq)
先求n的素因子p和q。由于n只有这2个因子,没有别的因子,所以p和q必然有一个小于,找到一个,另一个就知道了。用暴力法求p、q,用i循环从2到
(不能从1开始,因为1和本身就是一组因子对)一个个试。若n除以i的余数是0,i就是因子。
循环次数是,即十亿次计算。得到: p=891234941、q= 1123984201。RSA算法的p、q是1024位。从n=pq算出p、q,C++代码的执行时间约10秒,Python需要几分钟!
from math import *
n = 1001733993063167141
k = int(sqrt (n))
for i in range(2,k+1):# k+1是因为int是向下取整
if n%i== 0: print(i, n//i)(2)求e· (找到e使得de除(p-1)-(q-1)的余数为1)
下面代码打印出e = 823816093931522017。注意e有很多个,取最小的一个就行了。
(3)求X = mod n
本题考了快速幂
# e,n,C已知,求原文X
def fastPow(a, b, mod):
ans = 1
while b:
if b&1:ans = ans * a % mod
a = a*a % mod
b>>=1
return ans
n = 1001733993063167141
e = 823816093931522017
C = 20190324
print (fastPow(C, e,n))
#打印结果:5797069941123289492、矩阵快速幂
2.1矩阵乘法
- 一个m行n列(记为m×n)的矩阵,用二维数组matrix[ ][ ]来存储,matrix[i][i]是第i行第j列的元素。
- 两个矩阵A、B相乘,要求A的列数等于B的行数,设A是m×n,B是n×u,那么乘积C=AB的行和列是m×u的。
矩阵乘法C=AB:
for i in range(1,m+1): #i、j、k的先后顺序没关系,因为对于c[][]来说都一样
for j in range(1,u+1):
for k in range(1, n+1) :
c[i][j] += a[i][k] * b[k][j])例题四:矩阵相乘(模板题)
题目描述
输入两个矩阵,输出两个矩阵相乘的结果。
输入描述
输入的第一行包含三个正整数 N,M,K,表示一个 N×M的矩阵乘以一个的矩阵乘以一个M×K的矩阵。接下来的矩阵。接下来N行,每行M个整数,表示第一个矩阵。再接下来的个整数,表示第一个矩阵。再接下来的M行,每行K 个整数,表示第二个矩阵。
0<N,M,K≤100, 0≤ 矩阵中的每个数 ≤1000。
输出描述
输出有 N 行,每行 K 个整数,表示矩阵乘法的结果。
输入输出样例
输入
2 1 3 1 2 1 2 3输出
1 2 3 2 4 6
代码
n, m, k = map (int, input ().split())
A = []
B = []
C= [[0]*k for i in range(n)] # 用来存相乘后的矩阵
# 读入矩阵
for i in range(n): A.append(list(map(int, input().split()))) # 每次读一行,存到A
for i in range(m): B.append(list(map(int, input().split())))
# 矩阵相乘
for i in range(n):
for j in range(m):
for l in range(k):C[i][l] += A[i][j]*B[j][l]
# 输出矩阵
for i in range(n):
for j in range(k):
print(C[i][j],end="")
print() #换行2.2矩阵快速幂
若矩阵A是N×N的方阵,行数和列数都是N,它可以自乘,把n个A相乘记为.
矩阵的幂可以用快速幂来计算,从而极大提高效率,是常见的考题。
矩阵快速幂的复杂度:O()。其中N3是矩阵乘法,logn是快速幂。
出题的时候一般会给一个较小的N和一个较大的n,以考核快速幂的应用。
矩阵快速幂的原理和代码,与普通快速幂几乎一样。
2.3矩阵快速幂 和 快速幂 代码对比
def multi(A,B):
m1,n1 = len(A), len(A[0]) # len(矩阵):行数,len(矩阵[0]):列数
m2,n2 = len(B),len(B[0])
if n1 != m2: return None
C= [[0] *n2 for i in range(m1)]
for i in range(m1):
for k in range(n1) :
for j in range(n2):
C[i][j] += A[i][k]* B[k][j]
# 若需要取模运算:C[i][j] = (CLi][j] + A[i][k]* B[k][j])% mod
return C
def power(A,n): # A是矩阵
N = len(A)
ans = [[0]* N for i in range(N)] # 初始化答案矩阵
for i in range (N): ans[i][i] = 1 # 单位矩阵(对角线为1,其他为0)
while n:
if n % 2: # 若最后一位为1,等价于n&1
ans = multi(ans,A)
A = multi(A,A) # 倍增
n //= 2 # 右移一位,等价于n >>= 1
return ansdef fastPow(a, n, mod):
ans = 1
while n:
if n&1: ans = ans * a % mod
a = a * a % mod
n >>=1
return ans例题五:方阵次幂(模板题)
lanqiao0J题号1551
题目描述
给定一个 N 阶矩阵 A 和一个常数 M,请你输出 A 的 M 次幂。
输入描述
输入第一行包含两个整数 N,M。
接下来 N 行,每行包含 N 个数,表示矩阵 A。
1≤N≤30,0≤M≤5,0≤0≤ 矩阵中的每个数 ≤5。
输出描述
输出有 N 行,每行 N 个整数,表示
。
输入输出样例
输入
2 2 1 2 3 4输出
7 10 15 22
代码
def multi(A,B):
m1,n1 = len(A), len(A[0])
m2,n2 = len(B),len(B[0])
if n1 != m2: return None # 若不是方阵,返回无
C= [[0] *n2 for i in range(m1)]
for i in range(m1):
for k in range(n1) :
for j in range(n2):
C[i][j] += A[i][k]* B[k][j]
# 若需要取模运算:C[i][j] = (CLi][j] + A[i][k]* B[k][j])% mod
return C
def power(A,n): # A是矩阵
N = len(A)
ans = [[0]* N for i in range(N)] # 初始化答案矩阵
for i in range (N): ans[i][i] = 1 # 单位矩阵(对角线为1,其他为0)
while n:
if n % 2: # 若最后一位为1,等价于n&1
ans = multi(ans,A)
A = multi(A,A) # 倍增
n //= 2 # 右移一位,等价于n >>= 1
return ans
s,q =map(int,input().split()) # s行s列,q次幂
A=[]
for i in range(s):
A.append(list(map(int,input().split())))
res = power(A, q)
# 输出矩阵
for row in res:
for c in row:
print(c,end = ' ')
print()例题六:垒骰子
2015年第六届省赛,lanqiao0J题号132
题目描述
赌圣 atm 晚年迷恋上了垒骰子,就是把骰子一个垒在另一个上边,不能歪歪扭扭,要垒成方柱体。经过长期观察,atm 发现了稳定骰子的奥秘:有些数字的面贴着会互相排斥!
我们先来规范一下骰子:1 的对面是 4,2 的对面是 5,3 的对面是 6。
假设有 m 组互斥现象,每组中的那两个数字的面紧贴在一起,骰子就不能稳定的垒起来。
atm 想计算一下有多少种不同的可能的垒骰子方式。
两种垒骰子方式相同,当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。
由于方案数可能过多,请输出模
+7 的结果。
输入描述
输入第一行两个整数 n,m,n 表示骰子数目;
接下来 m 行,每行两个整数 a,b ,表示 a 和 b 数字不能紧贴在一起。
其中,0<n≤
,m≤36。
输出描述
输出一行一个数,表示答案模
+7 的结果。
输入输出样例
输入
2 1 1 2输出
544
思路
本题的n最大是,需要O(logn)的算法。
如何垒骰子?
先不考虑互斥问题,推理一下有多少种方案。
(1)1个骰子的情况。一个骰子有6个面,每个面朝上的时候侧面都可以旋转得到4个不同的摆放结果,共有4×6=24种。
(2)2个骰子的情况。一上一下两个骰子,共有(4×6)×(4×6)=576种。等等。
做法
从第1个骰子逐个往上垒,是一个递推关系,可以用动态规划来处理。
定义状态dp[i][i]:表示高度为i ,顶面点数为j的方案数。dp[i][j]等于i-1高度时所有与j的反面无冲突的方案数累加。
状态转移方程: j表示6个面
最后的总方案数乘以,因为每一个骰子可以4面转。
但是,如果直接这样编码,由于n很大,超时。
,把dp[ ][ ]转换成矩阵。
转换成矩阵乘法。垒n个骰子,等于n-1个转移矩阵相乘,最后再乘以第1个骰子 。

注:上面的的矩阵从前到后依次为从上到下的骰子,转移矩阵的每一列代表骰子朝上的数字1~6,最下面的骰子只有一列,代表骰子朝上的数字1~6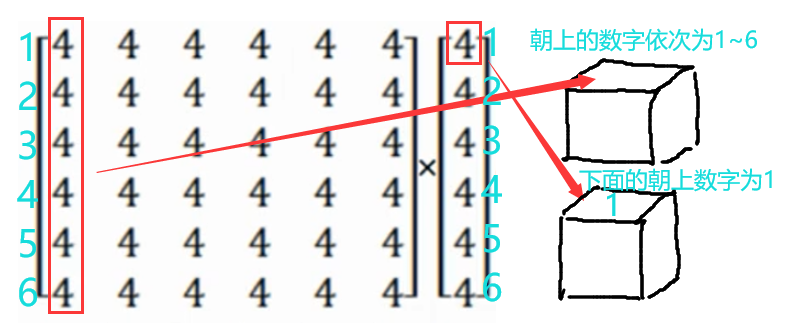
下面朝上的数字为1时,根据矩阵相乘,有种情况。
互斥:把转移矩阵中互斥的位置置为0
例: 数字1和数字4互斥,把转移矩阵中 第一行第四列和第一列第四行 置为0。若数字2和数字4互斥,把转移矩阵中 第二行第四列和第二列第四行 置为0。

代码
MOD = int(1e9+7) #注意一定要用int转换
def multi(A,B): #矩阵乘法
C = [[0]*6 for i in range(6)]
for i in range(6):
for j in range(6) :
for k in range(6) :
C[i][j] =int((C[i][j] +A[i][k]* B[k][j])% MOD)
return C
def power(A, n): #矩阵快速幂
res = [[0]*6 for i in range(6)]
for i in range(6): res[i][i] = 1
while n:
if n %2:res = multi (res,A)
A= multi(A,A)
n >>= 1
return res
def solve(n,dice) :
transfer = [[4]*6 for i in range(6)]# 转移矩阵
# # 去掉互斥的情况
for i in range(6):
for j in dice.get ((i+3)%6,[]): # 0对面是3,1对4,2对5
# get函数:若有键(i+3)%6,输出该键对应的值,没有该键,创建该键,赋值为[]
transfer[i][j]= 0
transfer = power(transfer,n-1) # 移矩阵乘n-1次
temp = [4]*6 # 表示最下面的骰子
ans = [0]*6
# 最后乘最下面的骰子
for i in range(6) :
for j in range(6):
ans[i] += transfer[i][j]* temp[j]
print(int(sum(ans)% MOD))
n, m= [int (str) for str in input ().split()]
# 用字典记录互相排斥的面
dice = dict()
for i in range(m) :
x,y = [int (str)-1 for str in input ().split()]
if x not in dice: dice[x] = [y]
else: dice[x].append(y)
if y not in dice: dice[y] =[x]
else: dice[y].append(x)
solve(n,dice)