一维最大连续子序列和

给你一个序列 【-1，-2，3，6，4，-9】的最大的连续的子序列和的值。

什么是最大连续子序列和，首先要满足两个条件：

1. 一定是连续的，例如 -1 3 4 都不是连续的。
2. 一定是最大的，-1 -2 3连续子序列的和为0，3 6 4连续子序列的和为13，很明显，我们取得maxnum=13

如何求解这一类问题呢？？

在这里只讲动态规划的思路。

---

定义dp数组 dp[i] 表示以i为当前下标的最长连续子序列的长度，注意这是一个长度值

给出动态规划的递推公式：

我们从前往后遍历数组（从后往前也可以，把i-1修改为i+1即可）。

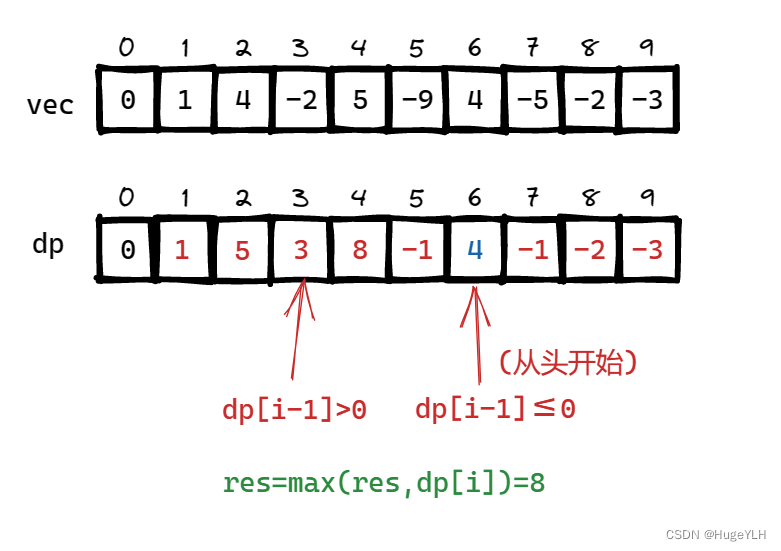
1. 如果前一个dp数组的元素不为正，则dp数组中记录了一个负数或者零，我们直接更新当前dp数组为新的元素（从头开始） ，赋值为vec[i]
2. 如果前一个dp数组的元素为正，则dp数组中记录了一定是一个正数，那么我们继续记录当前的元素，使得这个子序列达到最大值。

---

图片演示：

代码示例

//动态规划
void lengSquence2()
{
	int dp[10], res = 0;
	dp[1] = vec[1];
	for (int i = 2; i <= 6; i++)
	{
		if (dp[i - 1] <= 0)
		{
			dp[i] = vec[i];
		}
		else
		{
			dp[i] = vec[i] + dp[i - 1];
			res = max(res, dp[i]);
		}
	}
	cout << res << endl;
}

超简单写法：本质上也是动态规划的思想

//最大子序列和问题
void lengSquence1()
{
	int maxsum = 0, temp = 0;
	for (int i = 1; i <= 6; i++)
	{
		temp += vec[i];
		if (temp < 0)
		{
			temp = 0;
		}
		if (maxsum < temp)
		{
			maxsum = temp;
		}
	}
	cout << maxsum << endl;
}

---

二维最大连续子序列和、

例题：POJ1050
传送门：二维最大连续子序列和

我们需要得到一个二维的矩阵的最大的连续子矩阵和。

什么是最大连续子矩阵和？？

假设有这样一个矩阵：m=4 m*m

0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2

1. 在这个矩阵中，左下角的子矩阵的和是最大的，即9 2 … -4 1 … -1 8 这六个数字的和是最大的。
2. 因此 答案就是9 2 -4 1 -1 8，输出他们的答案为15

如果求二维矩阵的最大连续子矩阵的和呢？？？？

---

我们可以借助一维数组，将二维的问题转换为求解一维的问题

步骤：

1. 首先将二维矩阵的每一行，行高为1，进行求解一维最大子序列和：

2. 将二维矩阵的每两行合并，合并即两行对应的列数相加，合并为一行，行高为2，进行求解一维最大子序列和：

3. 将二维矩阵的每三行合并，行高为3，进行求解一维最大子序列和。
4. 将二维矩阵的每四行合并，行高为4，进行求解一维最大子序列和。

最后经过我们每一次合并后，我们每次都使用res记录最大值，便可以得到这一个连续的最大子矩阵的和。

代码示例

注意：时间复杂度O（N^3） 应该可以优化，在这里不在描述。

int n,m;
const int N=105;
int vec[N][N],dp[N],temp[N];
int res=0;
int get()
{
    /*
    一维数组求最大连续子序列
    */
    dp[1]=temp[1];
    int maxnum=0;
    for (int i=2;i<=n;i++)
    {
        if (dp[i-1]<=0)
        {
            dp[i]=temp[i];
        }
        else
        {
            dp[i]=dp[i-1]+temp[i];
            maxnum=max(maxnum,dp[i]);
        }
    }
    return maxnum;
}
int main()
{
	cin>>n;
    for (int i=1;i<=n;i++)
    {
        for (int j=1;j<=n;j++)
        {
            cin>>vec[i][j];
        }
    }
    for (int a=1;a<=n;a++)
    {
        //开始的行位置清零
        memset(temp,0,sizeof(temp));
        /*
        枚举一行的状态，二行的状态，三行的状态和四行的状态，每个状态利用temp数组转换为求一维的子序列和，求最大值
        */
        for (int i=a;i<=n;i++)
        {
            for (int j=1;j<=n;j++)
            {   
                temp[j]+=vec[i][j];
            }   
            res=max(res,get());
        }
    }
    
    cout<<res;
	return 0;
}