第八章数组

●前言

●一、数组是什么？

1.简要介绍

2.具体情况

●二、数组典型例题——一维&二维&三维

1.一维数组（校门外的树）

2.二维数组（彩票摇奖）

3.三维数组（工艺品制作）

●总结

前言

简单来说，数据结构是一种辅助程序设计并且进行优化的方法论，它不仅讨论数据的存储与处理的方法，同时也考虑到了数据彼此之间的关系与运算，从而极大程度的提高程序执行的效率，减少对内存空间的占用等。不同种类的数据结构适用于不同的程序应用，选择合适正确的数据结构，可以让算法发挥出更大的性能，给设计的程序带来更高效率的算法。

一、数组是什么？

1.简要介绍

数组类型是一种典型的静态数据结构，它使用了连续分配的内存空间去存储数据内容。静态数据结构是在编译时就给其变量分配好一定大小的内存空间。在建立静态数据结构的初期，必须事先去声明可能要占用多大的固定内存空间，因此这样可能造成一定的内存浪费或是经过后续操作出现数据溢出的现象。当对于简单的程序设计问题时，我们可以利用其下标，充分的对每一个位置上的数据进行修改、读取和使用，但是如果进行删除或插入数据的操作时将会移动大量的数据元素。

2.具体情况

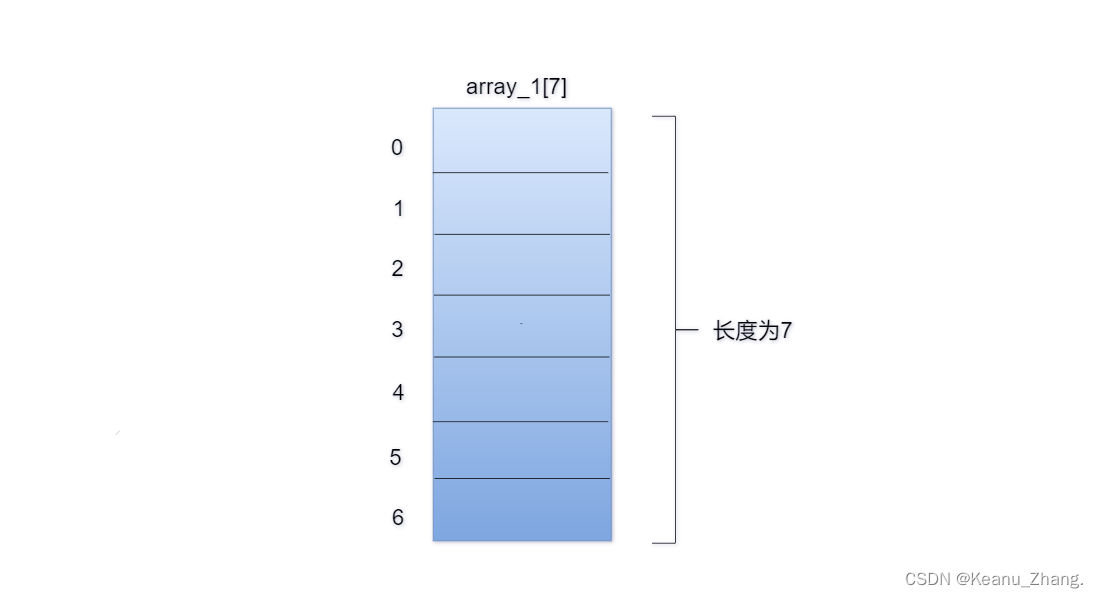
数组是具有相同和数据类型的变量的集合，它们在内存中占有一块连续的内存空间。数组可以分为一维数组、二维数组和多维数组，平时的学习中一维和二维是常用的，多维数组的话一般就会涉及到一些复杂的空间问题。在如下的图一中，是一个一维数组array_1[7],它是拥有6个相同数据类型的数组。

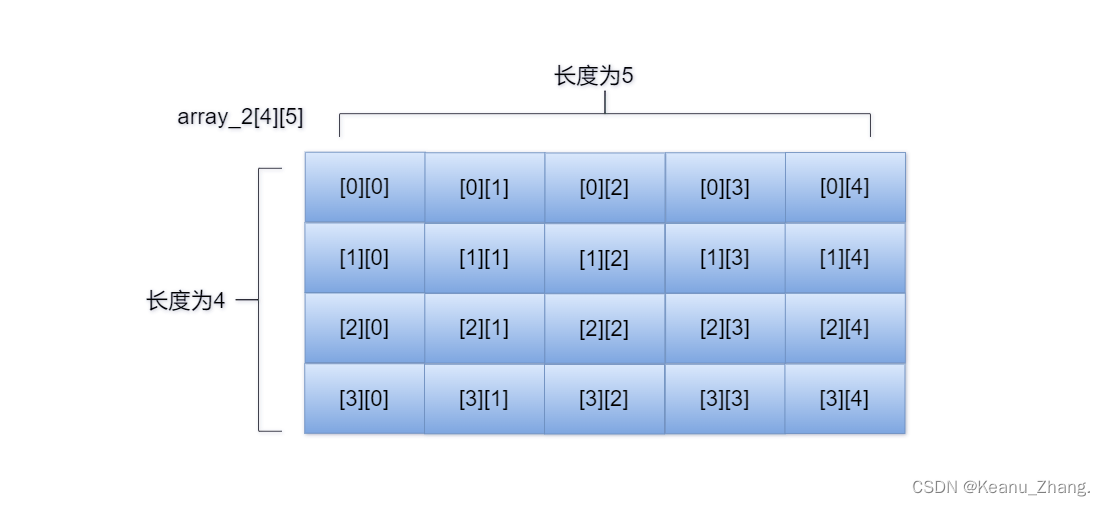
二维数组可以视为一维数组的扩展，它与一维数组差别只在于维数的声明。在如下的图二中，是一个二维数组array_2[4][5]在直观平面上的具体排列方式。

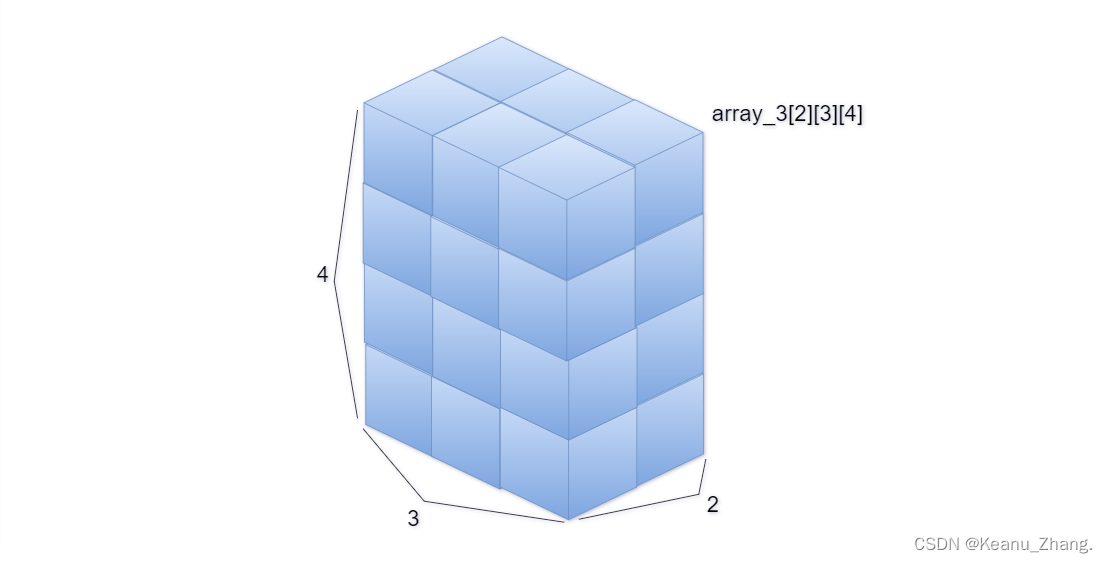
三维数组的表示法和二维数组一样，都可以视作一维数组的扩展。在如下的图三中，是一个三维数组array_3[2][3][4]将它想象成空间上的立方体的情况。

二、数组典型例题——一维&二维&三维

1.一维数组（校门外的树）

①例题：

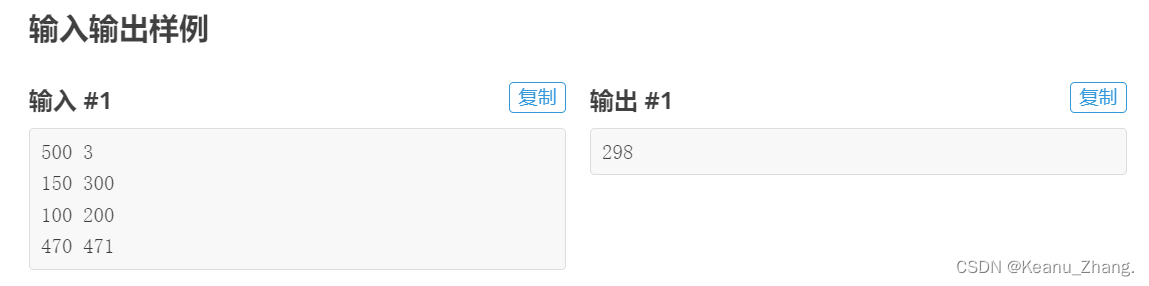
某校大门外长度为 l 的马路上有一排树，每两棵相邻的树之间的间隔都是 1 米。我们可以把马路看成一个数轴，马路的一端在数轴 0 的位置，另一端在 l 的位置；数轴上的每个整数点，即 0、1、2、...、l，都种有一棵树。
由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数，区域之间可能有重合的部分。现在要把这些区域中的树（包括区域端点处的两棵树）移走。你的任务是计算将这些树都移走后，马路上还有多少棵树。

输入要求：分析后可知需要输入马路的长度l，区域的数目m。m行的两个整数u和v，分别来表示一个区域的起点和终点坐标；

输出要求：输出一个整数，表示移走每个区域上的树后剩余的树的数目；

数据要求：1≤l≤10000、1≤m≤100、0≤u≤v≤l；

②代码展示：

#include<iostream>
using namespace std;
int tree_num[10001];
class tree {
public:
	int l,m;
	int u[101], v[101];
	void calculator()
	{
		for (int i = 0; i < m; i++)
		{
			for (int j = u[i]; j <= v[i]; j++)
			{
				tree_num[j] = 1;
			}
		}
		int count = 0;
		for (int k = 0; k <= l; k++)
		{
			if (tree_num[k] == 0)
				count++;
		}
		cout << "剩余" << count << "棵树" << endl;
	}
};
void text()
{
	tree t;
	cout << "请输入马路的长度:";
	cin >> t.l; 
	cout << "请输入区域的个数:";
	cin >> t.m;
	cout << "请开始分别输入" << t.m << "个区域的始点和终点坐标" << endl;
	for (int i = 0; i < t.m; i++)
	{
		cin >> t.u[i] >> t.v[i];
	}
	t.calculator();
}
int main()
{
	text();
}

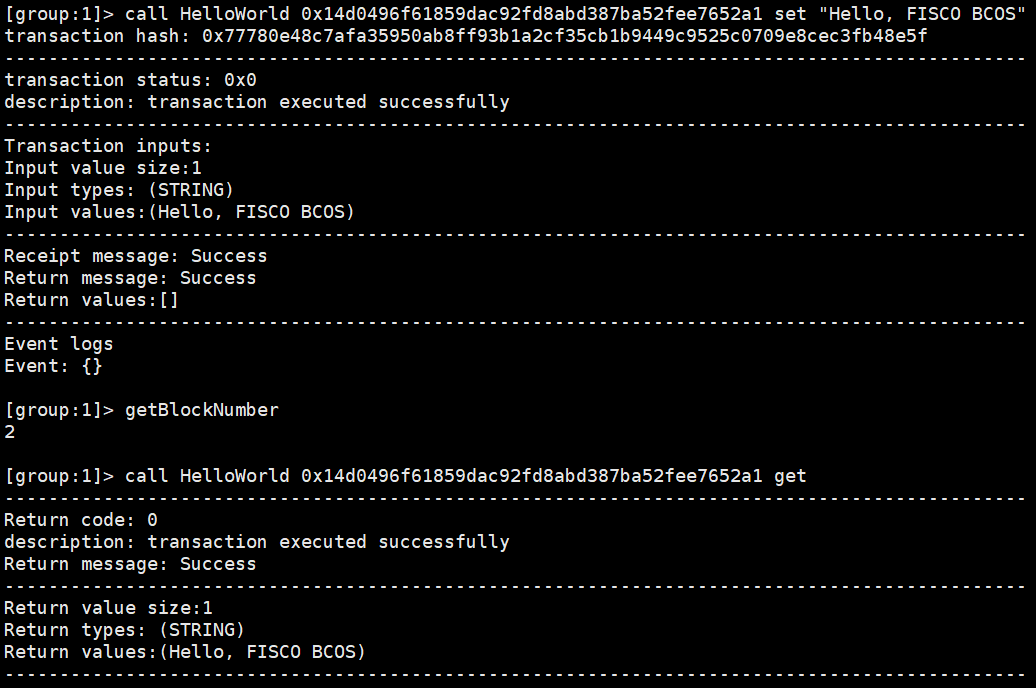
③代码结果展示：

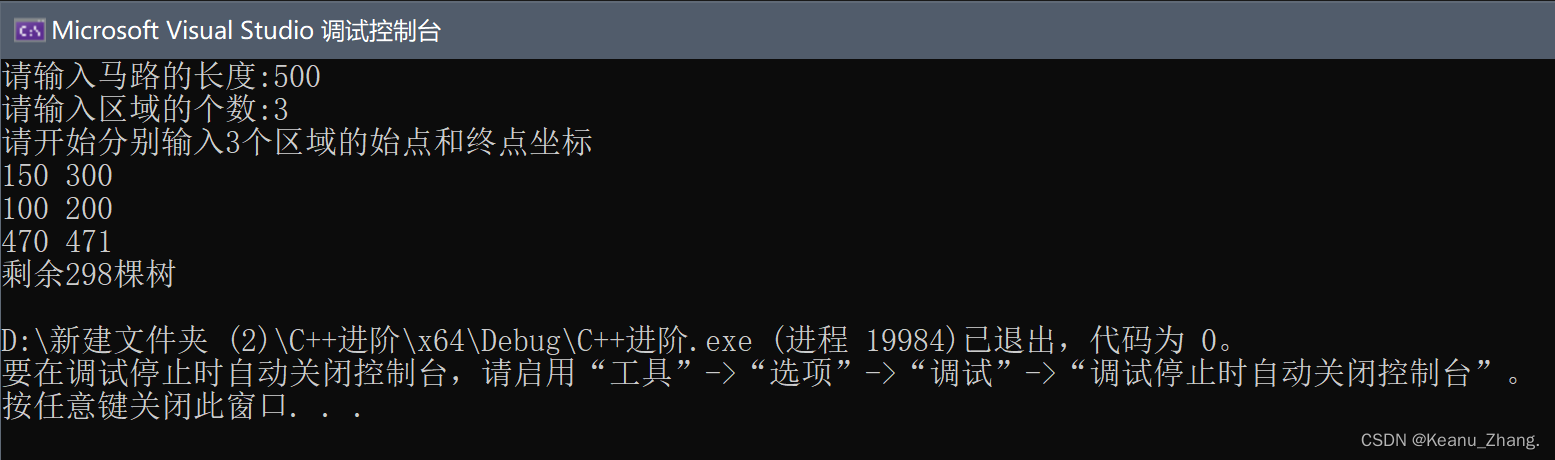
2.二维数组（彩票摇奖）

①例题：

为了丰富人民群众的生活、支持某些社会公益事业，北塔市设置了一项彩票。该彩票的规则是：

1. 每张彩票上印有 7 个各不相同的号码，且这些号码的取值范围为 1~33。
2. 每次在兑奖前都会公布一个由七个各不相同的号码构成的中奖号码。
3. 共设置 7 个奖项，特等奖和一等奖至六等奖。

兑奖规则如下：
        - 特等奖：要求彩票上 7 个号码都出现在中奖号码中。
        - 一等奖：要求彩票上有 6 个号码出现在中奖号码中。
        - 二等奖：要求彩票上有 5 个号码出现在中奖号码中。
        - 三等奖：要求彩票上有 4 个号码出现在中奖号码中。
        - 四等奖：要求彩票上有 3 个号码出现在中奖号码中。
        - 五等奖：要求彩票上有 2 个号码出现在中奖号码中。
        - 六等奖：要求彩票上有 1 个号码出现在中奖号码中。

注：兑奖时并不考虑彩票上的号码和中奖号码中的各个号码出现的位置。例如，中奖号码为 23、31、1、14、19、17、18，则彩票 12、8、9、23、1、16、7由于其中有两个号码（23和1）出现在中奖号码中，所以该彩票中了五等奖。现已知中奖号码和小明买的若干张彩票的号码，请你写一个程序帮助小明判断他买的彩票的中奖情况。

输入要求：输入的第一行只有一个自然数 n，表示小明买的彩票张数；第二行存放了 7 个介于 1 和 33 之间的自然数，表示中奖号码；在随后的 n 行中每行都有 7 个介于 1 和 33 之间的自然数，分别表示小明所买的 n 张彩票；

输出要求：依次输出小明所买的彩票的中奖情况（中奖的张数），首先输出特等奖的中奖张数，然后依次输出一等奖至六等奖的中奖张数。

数据要求：1≤n<1000

②代码展示：

#include<iostream>
using namespace std;
int number[1001];
class lottery {
public:
	int n;
	int arr_1[7];
	int arr_2[1001][7];
	void calculator_1()
	{
		for (int i = 0; i < n; i++)
		{
			int count = 0;
			int ans = 0;
			while (ans < 7)
			{
				for (int j = 0; j < 7; j++)
				{
					if (arr_2[i][j] == arr_1[ans])
						count++;
				}
				ans++;
			}
			number[i] = count;
		}
	}
	void calculator_2()
	{
		int a = 0, b = 0, c = 0, d = 0, e = 0, f = 0, g = 0;
		for (int i = 0; i < n; i++)
		{
			switch (number[i])
			{
			case 1:
				g++;
				break;
			case 2:
				f++;
				break;
			case 3:
				e++;
				break;
			case 4:
				d++;
				break;
			case 5:
				c++;
				break;
			case 6:
				b++;
				break;
			case 7:
				a++;
				break;
			}
		}
		cout << "分别对应中奖情况如下：(特等-一等-二等-三等-四等-五等-六等)" << endl;
		cout << a << " " << b << " " << c << " " << d << " " << e << " " << f << " " << g << endl;
	}
};
void text()
{
	lottery l;
	cout << "请输入购买彩票的张数：";
	cin >> l.n;
	cout << "请输入彩票的7位中奖号码：";
	for (int i = 0; i < 7; i++)
	{
		cin >> l.arr_1[i];
	}
	cout << "请输入购买彩票的号码：" << endl;
	for (int i = 0; i < l.n; i++)
	{
		for (int j = 0; j < 7; j++)
		{
			cin >> l.arr_2[i][j];
		}
	}
	l.calculator_1();
	l.calculator_2();
}
int main()
{
	text();
}

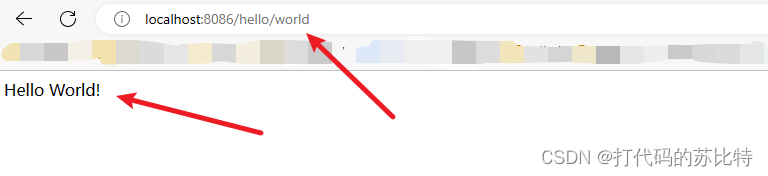
③代码结果展示：

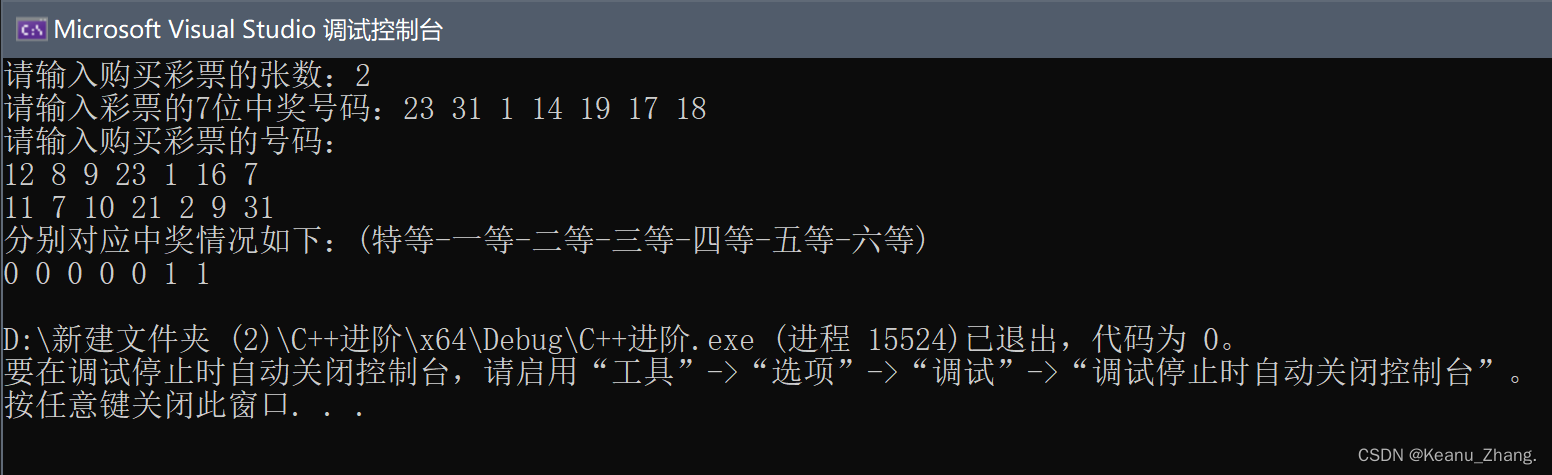
3.三维数组（工艺品制作）

①例题：

现有一个长宽高分别为 w,x,h 组成的实心玻璃立方体，可以认为是由 1✖1✖1 的数个小方块组成的，每个小方块都有一个坐标( i,j,k )。现在需要进行q次切割。每次切割给出 (x1,y1,z1),(x2,y2,z2)这6个参数，保证 x1<=x2,y1<=y2,z1<=z2；每次切割时，使用激光工具切出一个立方体空洞，空洞的壁平行于立方体的面，空洞的对角点就是给出的切割参数的两个点。

换句话说，所有满足 x1<=i<=x2 , y1<=j<=y2 , z1<=k<=z2 的小方块(i,j,k)的点都会被激光蒸发。例如有一个 4✖4✖4 的大方块，其体积为64；给出参数(1,1,1),(2,2,2)时，中间的8块小方块就会被蒸发，剩下56个小方块。现在想知道经过所有切割操作后，剩下的工艺品还剩下多少格小方块的体积。

输入要求：分别输入长宽高三个正整数w、x、h。一个整数q，然后在接下来的q行，每行6个整数（x1,y1,z1）,（x2,y2,z2）分别表示对角的两个顶点坐标；

输出要求：输出一个整数表示切割后还剩余多少个小立方体；

数据要求：1≤w,x,h≤20、1≤q≤100、1≤x1≤x2≤w、1≤y1≤y2≤x、1≤z1≤z2≤h；

②代码展示：

#include<iostream>
using namespace std;
#define max 21
int sq[max][max][max] = {0};
class art {
public:
	int w, x, h;
	int x1, y1, z1;
	int x2, y2, z2;
	void calculator_1()
	{
		for (int i = x1; i <= x2; i++)
			for (int j = y1; j <= y2; j++)
				for (int k = z1; k <= z2; k++)
					sq[i][j][k] = 1;
	}
	void calculator_2()
	{
		int count=0;
		for (int i = 1; i <= w; i++)
			for (int j = 1; j <= x; j++)
				for (int k = 1; k <= h; k++)
					if (sq[i][j][k] == 0)
						count++;
		cout << "剩余" << count << "个小方块" << endl;
	}
};
void text()
{
	art a;
	cout << "请输入长宽高：";
	cin >> a.w >> a.x >> a.h;
	cout << "请输入q的值:";
	int q; cin >> q;
	cout << "请分别输入两组对角点的坐标值" << endl;
	for (int num = 1; num <= q; num++)
	{
		 cin >> a.x1 >>a.y1 >> a.z1;
		 cin >> a.x2 >>a.y2>> a.z2;
		 a.calculator_1();
	}
	a.calculator_2();
}
int main()
{
	text();
}

③代码结果展示：