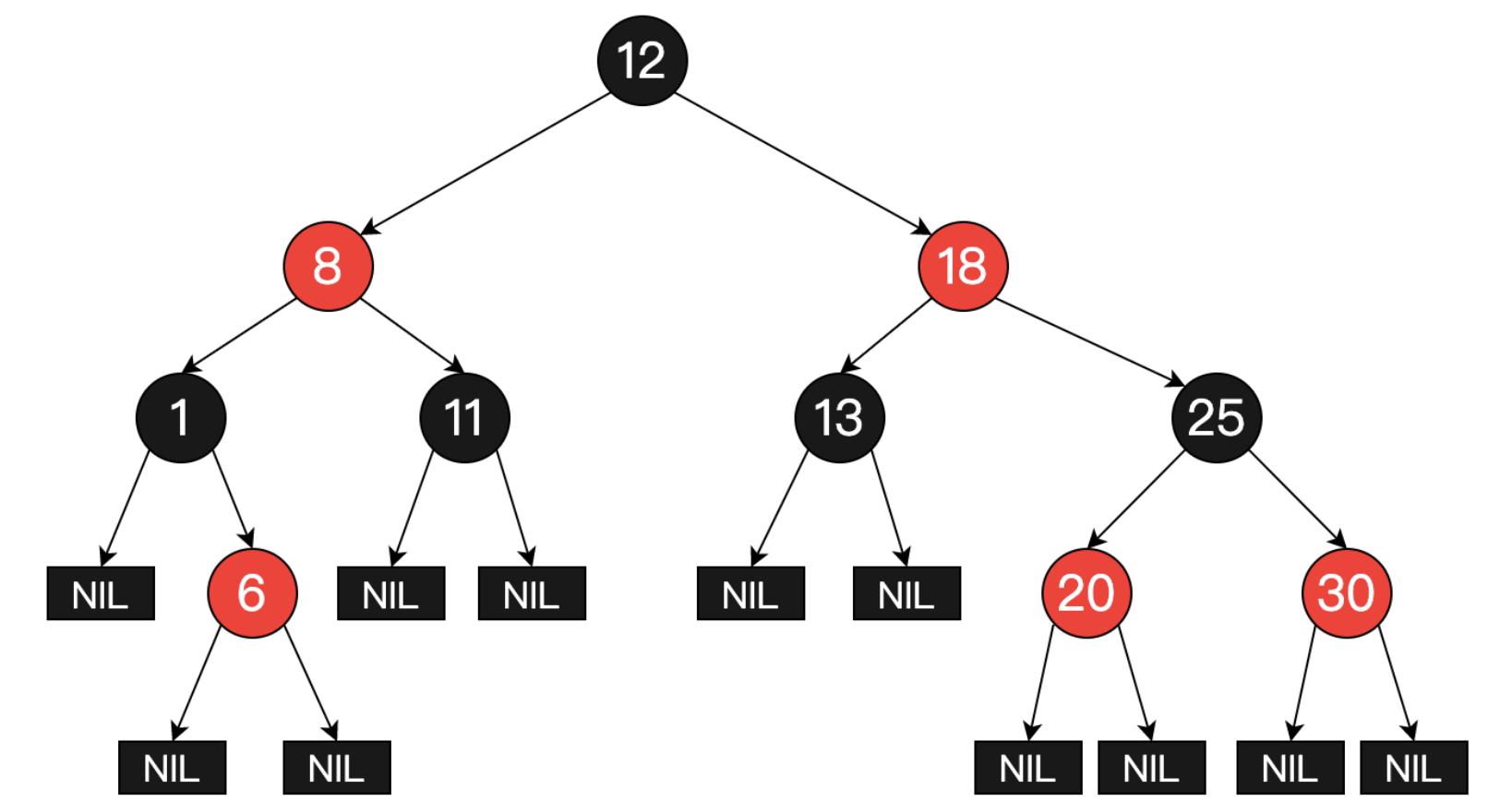
一.红黑树的定义
1.节点是红色或者黑色;
2.根节点和叶子节点是黑色,叶子节点为空节点;
3.每个红色节点的叶子节点都是黑色;
4.从任何节点到叶子节点的所有路径包含相同数目的黑色节点;
5.红黑树实现平衡和保持红黑特征的手段是:变色,左旋和右旋。
红黑树中从根节点到叶子节点的最长路径不多于最短路径的两倍长,所以红黑树大致平衡。
二.平衡二叉树
在二叉查找树的基础上,每个节点的左右子树高度差不超过1。频繁的插入和删除时需要多次旋转来维持平衡,牺牲大量时间。
三.区别
1.红黑树追求大致平衡,在和平衡二叉树查找时间复杂度相差不大的情况下,保证每次插入最多只用三次旋转就能达到平衡。
2.平衡二叉树追求绝对平衡,插入新节点时旋转的次数不能确定。