目录
连续信源的熵：
连续信源离散化后的概率空间：
连续信源离散化后的熵：
连续信源的绝对熵：
连续信源的相对熵：
连续信源的条件熵：
连续信源的相对条件熵：
连续信源相对熵的最大化：
峰值功率受限情况下的相对熵最大化条件：
均值受限情况下的相对熵最大化条件：
平均功率受限情况下的相对熵最大化条件：
加性高斯噪声信道的容量：
加性噪声信道的平均互信息：
加性高斯噪声(干扰)信道(AWGN)的信道容量：
香农公式：
信道容量和带宽的归一化分析：
归一化信道容量：单位时间单位频带内可达到的信息速率：
归一化信道带宽：单位信息速率所需要的最小带宽：
关于Eb/N0的归一化信道带宽：
例题：
连续信源的熵：
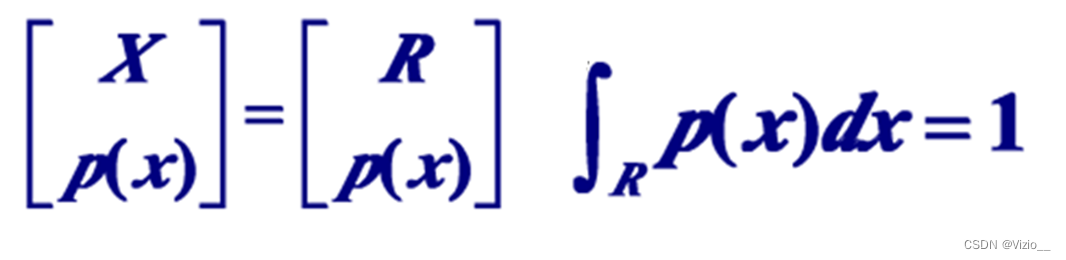
连续信源离散化后的概率空间：
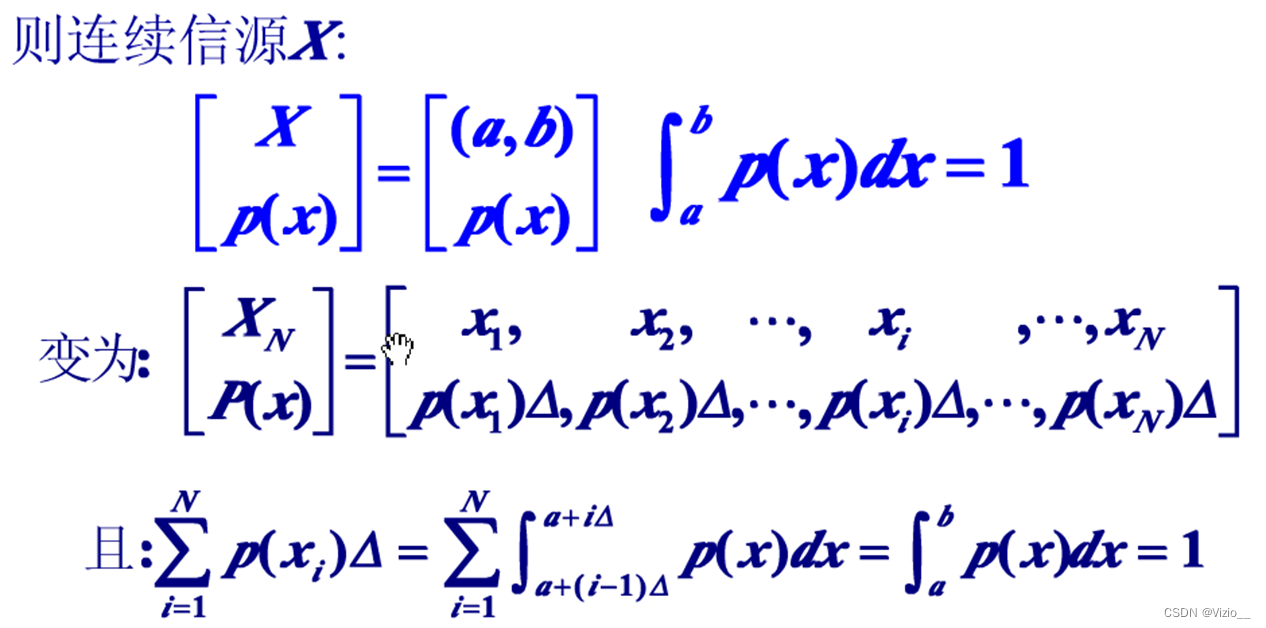
连续信源离散化后的熵：
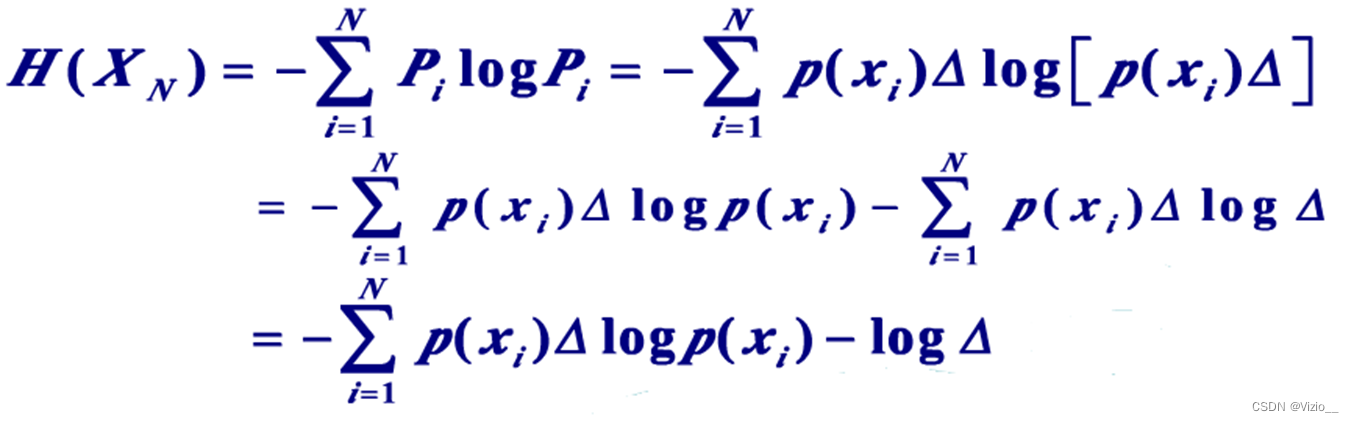
连续信源的绝对熵：
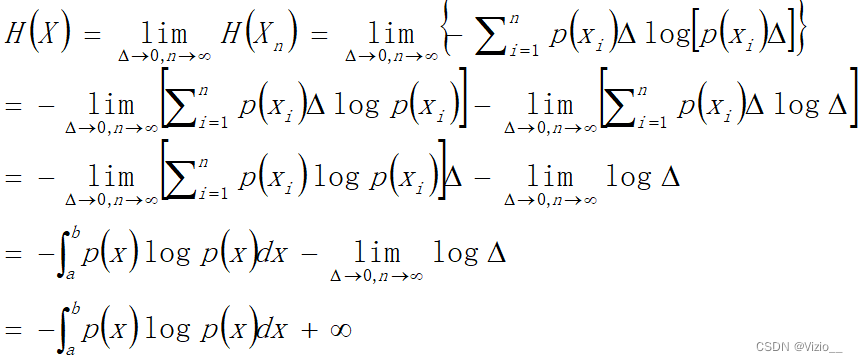
可见连续信源的熵无限大。该熵称为连续信源的绝对熵，无法确切地定义。
连续信源的相对熵：
连续信源的条件熵：
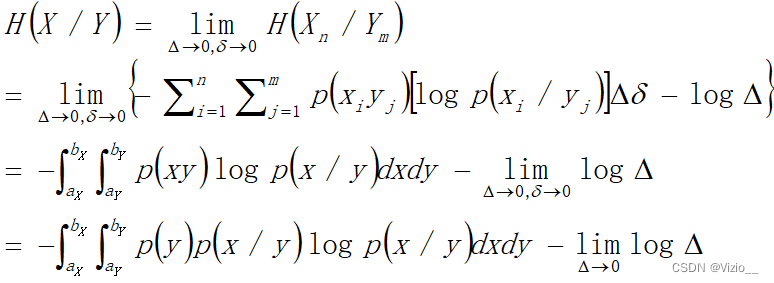
可见连续信源的条件熵取值无限大，同样无法确切定义；
要在一个容量有限的通信系统中传递连续信源的全部信息是不可能的；
连续信源的相对条件熵：
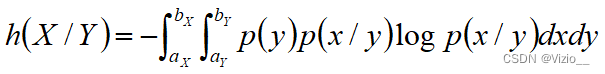
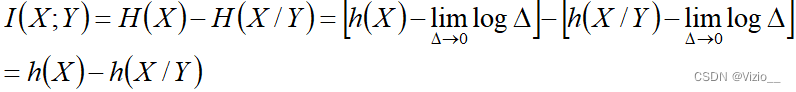
说明相对熵和相对条件熵的差值与普通的熵和条件熵的差值一样，仍然等于平均互信息量。
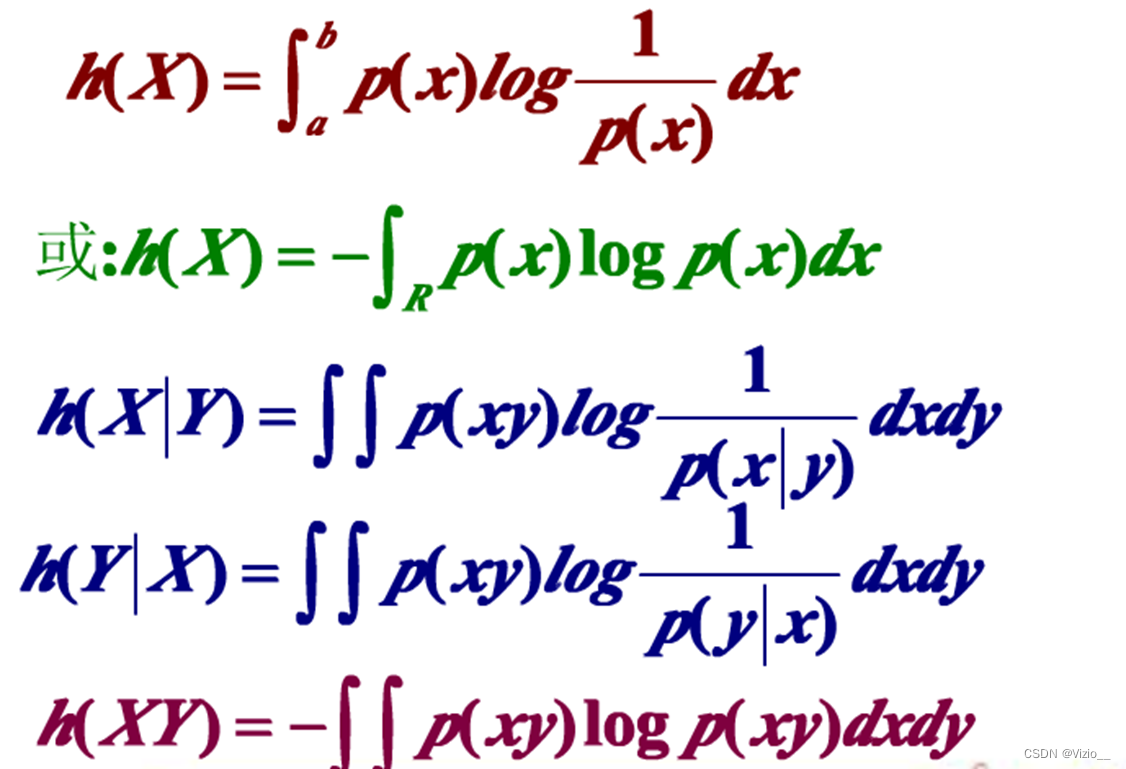
连续信源相对熵的最大化：
峰值功率受限情况下的相对熵最大化条件：
当连续信源的概率密度函数服从均匀分布时，该连续信源有最大的相对熵
均值受限情况下的相对熵最大化条件：
当连续信源的概率密度函数服从指数分布时，该连续信源有最大的相对熵
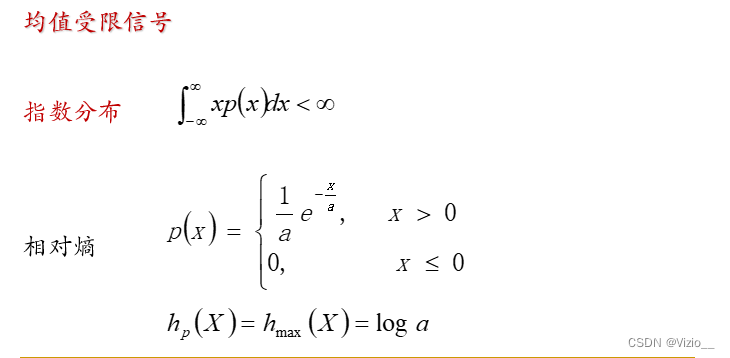
平均功率受限情况下的相对熵最大化条件：
当连续信源的概率密度函数服从高斯分布时，该连续信源有最大的相对熵
加性高斯噪声信道的容量：
加性高斯噪声(干扰)信道(AWGN)
信道输入：x 信道输出： y 加性高斯噪声：n
加性高斯噪声(干扰)的信道容量
已知通过信道后，从y可获得的关于x的平均互信息量
若已知信号x 的带宽为W , 对任意的这类信号则无失真无冗余的抽样频率应为：
(单位时间的样点数)单位时间内传输的信息量，即信息速率为
加性噪声信道的平均互信息：
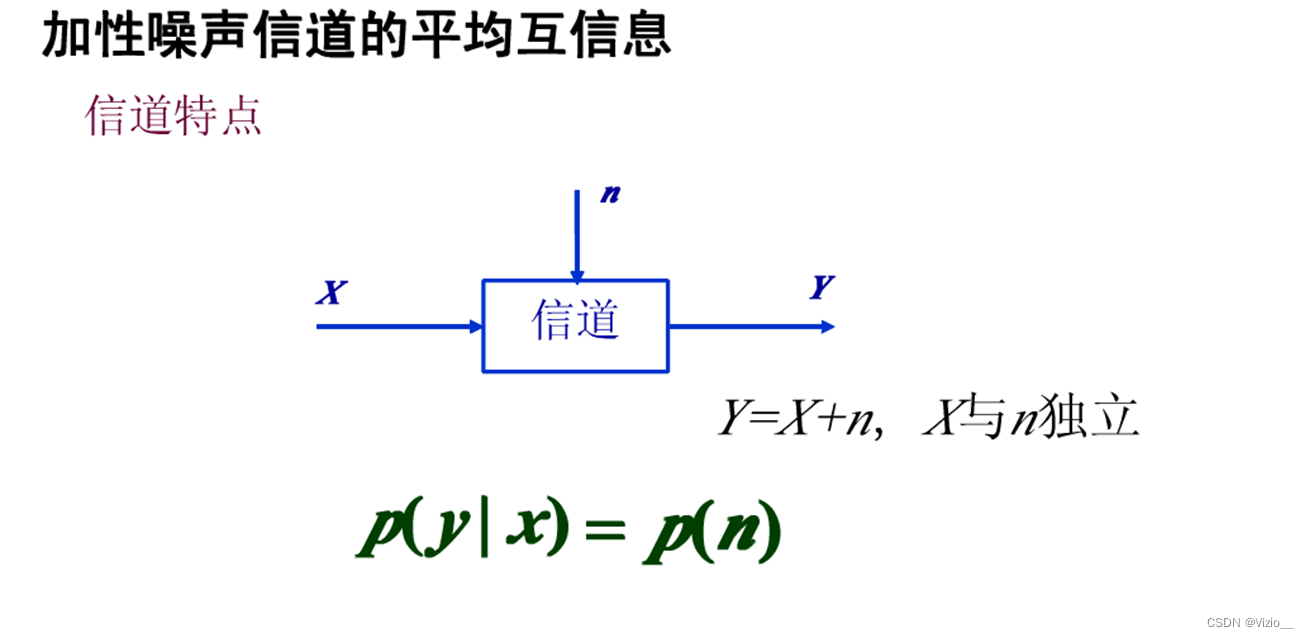
若已知信源x的统计特性，收到y后不可确定的部分为噪声的影响所导致。
根据雅可比行列式
加性高斯噪声(干扰)信道(AWGN)的信道容量：
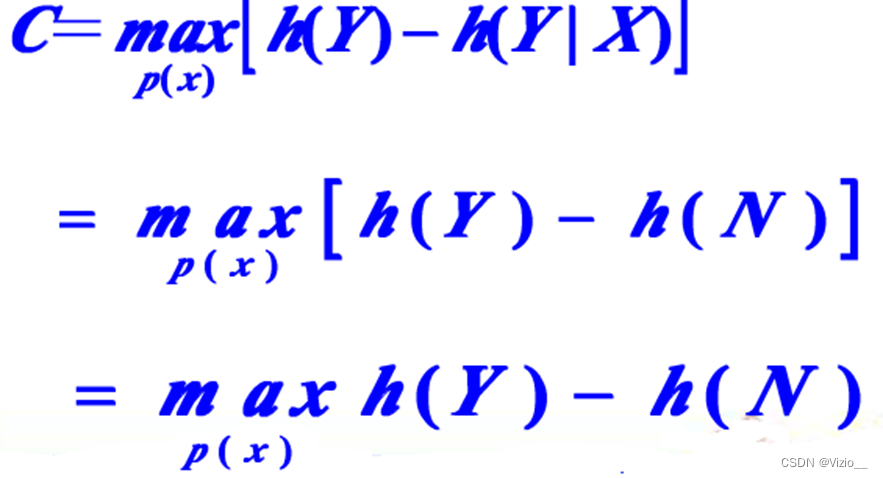
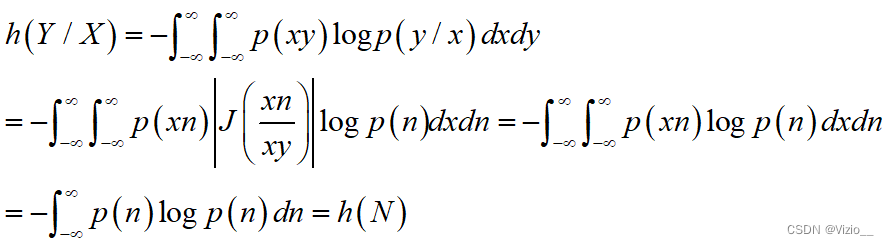
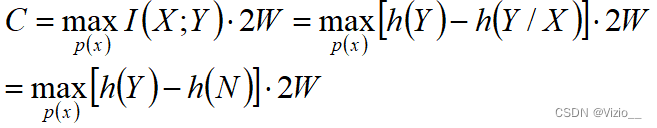
(1) 在均方受限的条件下，高斯分布的信源有最大的相对熵
(2) 两高斯分布的随机变量之和( y )仍为高斯随机变量
(3) 信号 x 与噪声 n 统计独立
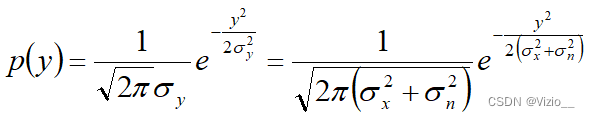
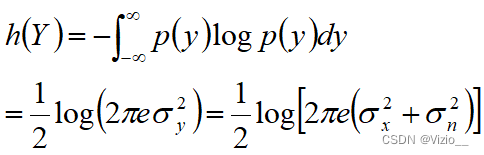
信道容量：
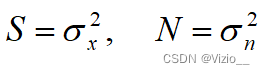
香农公式：
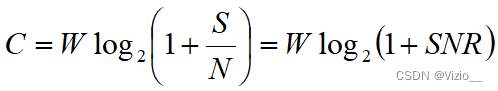
重要结论：
信道容量和带宽的归一化分析：
归一化信道容量：单位时间单位频带内可达到的信息速率：
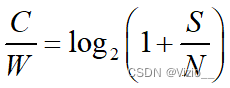
归一化信道带宽：单位信息速率所需要的最小带宽：
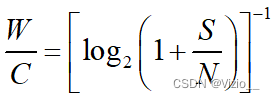
关于Eb/N0的归一化信道带宽：
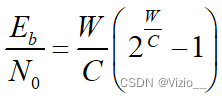
例题：
