MXNet的Faster R-CNN(基于区域提议网络的实时目标检测)《1》:论文源地址,克隆MXNet版本的源码,安装环境与测试,以及对下载的源码的每个目录做什么用的,做个解释。
MXNet的Faster R-CNN(基于区域提议网络的实时目标检测)《2》:对论文中的区域提议、平移不变锚、多尺度预测等概念的了解,对损失函数、边界框回归的公式的了解,以及共享特征的训练网络的方法。
MXNet的Faster R-CNN(基于区域提议网络的实时目标检测)《3》:加载模型参数,给目标加锚框可视化操作,对参数文件的了解,以及感兴趣区域ROI和泛洪填充的方法(FLOODFILL_FIXED_RANGE,FLOODFILL_MASK_ONLY)
MXNet的Faster R-CNN(基于区域提议网络的实时目标检测)《4》:下载与熟悉Pascal VOC2007,2012语义分割数据集,明白实例分割除了分类之外,还可以细分到像素级别的所属类别。
MXNet的Faster R-CNN(基于区域提议网络的实时目标检测)《5》:主要就是熟悉转置卷积与大家所熟知的卷积有什么区别,作用是什么,以及双线性插值等相关知识
MXNet的Faster R-CNN(基于区域提议网络的实时目标检测)《6》:主要讲解关于参数解析的安全执行(ast.literal_eval),ROI池化以及计算图的可视化的处理
MXNet的Faster R-CNN(基于区域提议网络的实时目标检测)《7》:打印内容(比如参数文件里的东西)的三种方式以及对奇异值分解(SVD,Singular Value Decomposition)的熟悉,了解SVD的作用和运用
MXNet的Faster R-CNN(基于区域提议网络的实时目标检测)《8》:主要是通过参数的设置进一步熟悉模型,以及对于符号式编程的复习,另外关于损失函数之类,这里用到了自定义评价函数,然后通过自带的mx.metric来做,有示例让大家熟悉。
从上面的文章一路看过来的伙伴们,应该对这个框架有一定的了解了,这里先概括下整体是怎么个大概流程,当然在前面的可视化当中也可以具体知道。
首先输入数据进入到多层卷积神经网络,通过Conv--relu--Pooling获取特征图,这些特征图是用来给后续的区域提议网络RPN(Region Proposal Networks)和全连接层(Fully Conneted Layers)使用的。
我们知道这个RPN是用来生成区域提议(region proposals)的,通过Softmax判断锚框是正类锚框还是负类锚框,然后利用边界框回归来修正锚框获得精确的提议。
在MXNet的Faster R-CNN(基于区域提议网络的实时目标检测)《6》 这节我们介绍了ROI池化,这层收集输入的特征图和proposals提议,通过这些信息提取提议特征图(proposal feature maps),最后输入到全连接层判定目标类别。
最后我们利用上面获取到的提议特征图计算proposal的类别,同时再次使用边界框回归(bounding box regression)获得检测框最终的精确位置。
这节我们从test.py测试模型来了解下有哪些相关知识点,由于配置低在训练的时候没法训练,在测试的时候也只能将test_net(sym, imdb, args)注释掉,但不影响我们接下来的学习,我们先来看下这个加载的测试数据方法TestLoader
测试命令:python test.py --dataset voc --network vgg16 --params model/vgg16-0010.params
# 加载测试数据
test_data = TestLoader(imdb.roidb, batch_size=1, short=args.img_short_side, max_size=args.img_long_side,
mean=args.img_pixel_means, std=args.img_pixel_stds)然后我们查看TestLoader,这个类class TestLoader(mx.io.DataIter)的参数是一个MXNet的迭代基类mx.io.DataIter
MXNet中的所有I/O都由该类的专门化处理。通过调用next来返回DataBatch,然后我们接着TestLoader往下看可以看到,它的属性、方法以及我们需要关注的next方法中的getdata方法,这个获取数据的方法出现im_tensor = mx.nd.array(tensor_vstack(im_tensor, pad=0))这个tensor_vstack方法。接下来会专门介绍它!
张量的垂直叠加
这个张量的垂直叠加,跟numpy中自带的np.vstack有区别,我们贴出源码:
def tensor_vstack(tensor_list, pad=0):
"""
通过添加一个新轴来垂直叠加张量
:tensor_list: 张量列表
:pad: 填充的值
:返回最大形状张量
"""
if len(tensor_list) == 1:
return tensor_list[0][np.newaxis, :]
ndim = len(tensor_list[0].shape)
dimensions = [len(tensor_list)] # first dim is batch size
for dim in range(ndim):
dimensions.append(max([tensor.shape[dim] for tensor in tensor_list]))
dtype = tensor_list[0].dtype
if pad == 0:
all_tensor = np.zeros(tuple(dimensions), dtype=dtype)
elif pad == 1:
all_tensor = np.ones(tuple(dimensions), dtype=dtype)
else:
all_tensor = np.full(tuple(dimensions), pad, dtype=dtype)
if ndim == 1:
for ind, tensor in enumerate(tensor_list):
all_tensor[ind, :tensor.shape[0]] = tensor
elif ndim == 2:
for ind, tensor in enumerate(tensor_list):
all_tensor[ind, :tensor.shape[0], :tensor.shape[1]] = tensor
elif ndim == 3:
for ind, tensor in enumerate(tensor_list):
all_tensor[ind, :tensor.shape[0], :tensor.shape[1], :tensor.shape[2]] = tensor
else:
raise Exception('Sorry, unimplemented.')
return all_tensor如果是在这个源码当中测试的话,也可以直接使用from symdata.image import tensor_vstack导入即可。从代码得知,按照最大形状来垂直叠加张量,一维变二维、二维变三维、三维变四维。
这里默认的填充是0,如果指定了其他值的话,填充的就是指定的值。我们来看几个示例:
a=np.array([[1,2,3,4],[7,8,9,10]])
b=np.array([[11,22,33,44],[77,88,99,1010],[333,444,555,666]])
np_vstack=np.vstack((a,b))
print(type(np_vstack),np_vstack.shape)#<class 'numpy.ndarray'> (5, 4)
print(np_vstack)
'''
[[ 1 2 3 4]
[ 7 8 9 10]
[ 11 22 33 44]
[ 77 88 99 1010]
[ 333 444 555 666]]
'''这个是np的张量的垂直堆叠,跟np.concatenate((a,b))效果一样。我们看到的形状是(5,4),二维的,维度是没有变化的!
接下来我们测试上面的函数tensor_vstack有什么不一样,从参数(tensor_list, pad=0)我们看出,是张量的列表,也就是说,列表里面的元素是由张量构成。
c=[]
c.append(a)
c.append(b)
print(c)
'''
[array([[ 1, 2, 3, 4],
[ 7, 8, 9, 10]]), array([[ 11, 22, 33, 44],
[ 77, 88, 99, 1010],
[ 333, 444, 555, 666]])]
'''
t_vstack=tensor_vstack(c)
print(type(t_vstack),t_vstack.shape)#<class 'numpy.ndarray'> (2, 3, 4)
print(t_vstack)
'''
[[[ 1 2 3 4]
[ 7 8 9 10]
[ 0 0 0 0]]
[[ 11 22 33 44]
[ 77 88 99 1010]
[ 333 444 555 666]]]
'''这里出来的是三维数组了,其中里面的张量的形状是一样的,都是(3,4),其中第一个只有两行,于是最后一行使用0填充。
我们再添加一个二维数组来看下有什么变化:
c.append(np.array([[4,2,1,6]]))
t_vstack=tensor_vstack(c)
print(type(t_vstack),t_vstack.shape)#<class 'numpy.ndarray'> (3, 3, 4)
print(t_vstack)
'''
[[[ 1 2 3 4]
[ 7 8 9 10]
[ 0 0 0 0]]
[[ 11 22 33 44]
[ 77 88 99 1010]
[ 333 444 555 666]]
[[ 4 2 1 6]
[ 0 0 0 0]
[ 0 0 0 0]]]
'''添加的这个1行4列,同样将变换成3行4列,其余两行都使用0填充。
回过来看,这个方法提供到了三维的数组是吧,然后我们看下三维生成四维的效果:
a=np.array([[[1,2,3,4],[7,8,9,10]]])#(1,2,4)
b=np.array([[[11,22,33,44],[77,88,99,1010],[333,444,555,666]]])#(1, 3, 4)
c=[]
c.append(a)
c.append(b)
c.append(np.array([[[4,2,1,6]]]))#再添加一个(1,1,4)
t_vstack=tensor_vstack(c)
print(type(t_vstack),t_vstack.shape)#<class 'numpy.ndarray'> (3, 1, 3, 4)
print(t_vstack)
'''
[[[[ 1 2 3 4]
[ 7 8 9 10]
[ 0 0 0 0]]]
[[[ 11 22 33 44]
[ 77 88 99 1010]
[ 333 444 555 666]]]
[[[ 4 2 1 6]
[ 0 0 0 0]
[ 0 0 0 0]]]]
'''三个三维的数组就这样愉快的垂直堆叠在了一起,变换成了四维的数组,形状为(3,1,3,4)的张量,其中不够的行列,就使用0填充了,如果使用其他值,比如用1来填充,只需指定pad参数即可:tensor_vstack(c,pad=1)
这样做的目的是使得不同样本数的输入,可以让它们变得形状一样(通过填充),然后垂直堆叠起来形成一个增加一个维度的张量,便于计算。
我们接着从上到下的顺序来看下每个文件都涉及到了哪些需要学习的知识点,symdata/anchor.py包含两个类AnchorGenerator和AnchorSampler。
AnchorGenerator:生成锚框,锚框数是按照len(anchor_scales) * len(anchor_ratios)【锚框尺度*锚框比例】,这里是3*3=9,也就是在特征图上面是按照这个尺度与比例来生成锚框的,由于特征图是原图抽取的,比如缩小了16倍,那我们需要扩大16倍以及做一些形状变换,得到所有的锚框数,当然具体的细节在最后一篇结束的文章里我将会把源码全部放到github以及有详细的注释,便于帮助大家更快的理解,当然由于水平有限,错误在所难免,欢迎大家指出。
AnchorSampler:锚框采样器,主要就是筛选的作用,保留大于交并比阈值(0.7)的前景锚框和小于交并比阈值0.3的背景锚框,找出最接近真实框的锚框。
交并比IoU的计算
锚框的筛选,需要用到交并比IoU这样一个很关键的方法,也就是衡量锚框跟真实框的交集,重叠部分越多,表示效果越好,越接近真实框,那这个交并比就是交集与并集的比值,另外这里需要注意的是这个坐标值的问题,跟数学中的坐标有区别,计算机里面一般都是从左上角开始的,也就是说往右和往下都是正的值,这点需要注意。
我们来看下symdata/bbox.py里面的交并比方法bbox_overlaps:
def bbox_overlaps(boxes, query_boxes):
"""
determine overlaps between boxes and query_boxes
:param boxes: n * 4 bounding boxes
:param query_boxes: k * 4 bounding boxes
:return: overlaps: n * k overlaps
"""
n_ = boxes.shape[0]
k_ = query_boxes.shape[0]
overlaps = np.zeros((n_, k_), dtype=np.float64)
for k in range(k_):
query_box_area = (query_boxes[k, 2] - query_boxes[k, 0] + 1) * (query_boxes[k, 3] - query_boxes[k, 1] + 1)
print(query_box_area)
for n in range(n_):
iw = min(boxes[n, 2], query_boxes[k, 2]) - max(boxes[n, 0], query_boxes[k, 0]) + 1
if iw > 0:
ih = min(boxes[n, 3], query_boxes[k, 3]) - max(boxes[n, 1], query_boxes[k, 1]) + 1
if ih > 0:
box_area = (boxes[n, 2] - boxes[n, 0] + 1) * (boxes[n, 3] - boxes[n, 1] + 1)
all_area = float(box_area + query_box_area - iw * ih)
overlaps[n, k] = iw * ih / all_area
return overlaps两个锚框的维度是2维,形状是(左上角坐标x1,y1,右下角坐标x2,y2),N*4的锚框。
我们来测试下这个2组锚框的交并比是怎么样的:
a=np.array([[0,0,100,100],[0,0,200,120]])
b=np.array([[10,10,110,110],[80,80,220,280]])
print(bbox_overlaps(a,b))
'''
[[0.68319446 0.0115745 ]
[0.41943177 0.10400201]]
'''交并比的个数就是a.shape[0]*b.shape[0]
大家如果稍微细心点,就会发现,query_boxes[k, 2] - query_boxes[k, 0] + 1等其他位置都有+1,这个表示的是边框线的像素。那如果是没有+1的话,计算结果如下,我们来看下结果:
a=np.array([[0,0,5,5]])
b=np.array([[1,1,6,6]])
print(bbox_overlaps(a,b))#[[0.47058824]]这个大家手动也可以验证下,没有问题。
我们通过画矩形框图来直观感受下,上面是两组锚框(a是生成的锚框,b是真实锚框),然后a中的锚框分别与b中的锚框做IoU
from PIL import ImageDraw,Image
img = Image.open("1.jpg")#为了让锚框显示更清晰,使用一张白色背景图片
draw = ImageDraw.Draw(img)
img_boxes = np.concatenate((a,b))
color = [(0,0,0),(255,255,0),(255,0,255),(255,0,0),(0,0,255)]
i=0
for box in img_boxes:
x1,y1,x2,y2 = box
if i==5:
i=0
draw.rectangle([x1,y1,x2,y2],outline=color[i],width=4)
i=i+1
img.show()如下图:
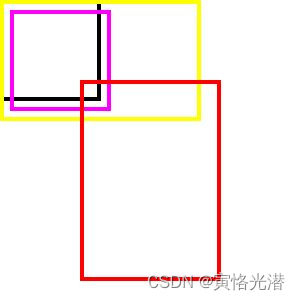
这里的a是黑色框和黄色框,b是粉色框与红色框,我们可以看到它们的交集(黑框与粉色、红色的交并比,黄框与粉色、红色的交并比)和对比上面输出的IoU的值,这样就很清晰明了了。
裁剪越界的锚框
生成的锚框会存在一些超出图片边界的锚框,这个时候我们做一个裁剪的操作,将超过了图片宽高边界的部分去掉!这里比较简单,直接看代码:
def clip_boxes(boxes, im_shape):
"""
裁剪掉超出图片边界的锚框部分
:param boxes: [N, 4* num_classes]
:param im_shape: 高宽元组
:return: [N, 4* num_classes]
"""
# x1 >= 0
boxes[:, 0::4] = np.maximum(np.minimum(boxes[:, 0::4], im_shape[1] - 1), 0)
# y1 >= 0
boxes[:, 1::4] = np.maximum(np.minimum(boxes[:, 1::4], im_shape[0] - 1), 0)
# x2 < im_shape[1]
boxes[:, 2::4] = np.maximum(np.minimum(boxes[:, 2::4], im_shape[1] - 1), 0)
# y2 < im_shape[0]
boxes[:, 3::4] = np.maximum(np.minimum(boxes[:, 3::4], im_shape[0] - 1), 0)
return boxes边界框回归
对于边界框回归我们在 MXNet的Faster R-CNN(基于区域提议网络的实时目标检测)《2》 这篇文章中有讲到这个边界框回归的公式,有兴趣的可以去看看,然后我们来看下实际的代码:
def bbox_transform(ex_rois, gt_rois, box_stds):
"""
计算从ex_rois到gt_rois的边界框回归目标(锚框到真实边界框的边界框回归)
:param ex_rois: [N, 4]
:param gt_rois: [N, 4]
:return: [N, 4]
"""
assert ex_rois.shape[0] == gt_rois.shape[0], 'inconsistent rois number'
# 预测锚框的宽高与中心位置
ex_widths = ex_rois[:, 2] - ex_rois[:, 0] + 1.0
ex_heights = ex_rois[:, 3] - ex_rois[:, 1] + 1.0
ex_ctr_x = ex_rois[:, 0] + 0.5 * (ex_widths - 1.0)
ex_ctr_y = ex_rois[:, 1] + 0.5 * (ex_heights - 1.0)
# 真实框的宽高与中心位置
gt_widths = gt_rois[:, 2] - gt_rois[:, 0] + 1.0
gt_heights = gt_rois[:, 3] - gt_rois[:, 1] + 1.0
gt_ctr_x = gt_rois[:, 0] + 0.5 * (gt_widths - 1.0)
gt_ctr_y = gt_rois[:, 1] + 0.5 * (gt_heights - 1.0)
targets_dx = (gt_ctr_x - ex_ctr_x) / (ex_widths + 1e-14) / box_stds[0] #平移量
targets_dy = (gt_ctr_y - ex_ctr_y) / (ex_heights + 1e-14) / box_stds[1] #平移量
targets_dw = np.log(gt_widths / ex_widths) / box_stds[2] #尺度因子
targets_dh = np.log(gt_heights / ex_heights) / box_stds[3] #尺度因子
targets = np.vstack((targets_dx, targets_dy, targets_dw, targets_dh)).transpose()
return targets当然我们从它的代码实践中可以看到,box_stds标准差都设置成了1.0,所以可以忽略,这样对比公式就更清晰了。相当于是从预测锚框先通过平移然后缩放来接近真实锚框,输出的就是(targets_dx, targets_dy, targets_dw, targets_dh)这样的平移量和尺度因子,这就对预测锚框进行了修正!
NMS非极大值抑制
非极大值抑制的目的是去掉很多重复(交并比比较大)的边界框,首先找出类别分数最大的(降序排序),然后跟其他的边界框进行交并比IoU的计算,如果其值大于设定的阈值就忽略掉,只保留交并比小于阈值的,这样一直循环直到将所有的边界框都比较全部完为止。
贴出代码来看下:
def nms(dets, thresh):
"""
greedily select boxes with high confidence and overlap with current maximum <= thresh
rule out overlap >= thresh
:param dets: [[x1, y1, x2, y2 score]]
:param thresh: retain overlap < thresh
:return: indexes to keep
"""
x1 = dets[:, 0]
y1 = dets[:, 1]
x2 = dets[:, 2]
y2 = dets[:, 3]
scores = dets[:, 4]# 最后一列的分数
areas = (x2 - x1 + 1) * (y2 - y1 + 1)
order = scores.argsort()[::-1]# 降序
keep = []
while order.size > 0:
i = order[0]
keep.append(i)
xx1 = np.maximum(x1[i], x1[order[1:]])
yy1 = np.maximum(y1[i], y1[order[1:]])
xx2 = np.minimum(x2[i], x2[order[1:]])
yy2 = np.minimum(y2[i], y2[order[1:]])
w = np.maximum(0.0, xx2 - xx1 + 1)
h = np.maximum(0.0, yy2 - yy1 + 1)
inter = w * h
ovr = inter / (areas[i] + areas[order[1:]] - inter)
inds = np.where(ovr <= thresh)[0]
order = order[inds + 1]
return keep然后我们示例4个边界框(带上类别分数)来测试下这个效果:
dets=np.array([[10, 10, 100, 100, 0.61],[5, 20, 100, 100, 0.88],[20, 80, 188, 180, 0.66],[150, 150, 200, 200, 0.55]])
print(nms(dets=dets,thresh=0.7))#[1, 2, 3]按照分数从大到小排序(0.88,0.66,0.61,0.55)对应的索引值是(2,0,1,3),0.88分数的框跟余下的框进行交并比计算。结果就只剩下了索引值为1,2,3的锚框了
因为第一个跟第二个锚框的重复度很高,大于了设置的阈值,所以去掉第一个,我们也可以使用上面的画图方法来更直观的看下:
from PIL import ImageDraw,Image
img = Image.open("1.jpg")#为了让锚框显示更清晰,使用一张白色背景图片
draw = ImageDraw.Draw(img)
img_boxes = dets[:,0:4]#去掉分数列
color = [(0,0,0),(255,255,0),(255,0,255),(255,0,0),(0,0,255)]
i=0
for box in img_boxes:
x1,y1,x2,y2 = box
if i==5:
i=0
draw.rectangle([x1,y1,x2,y2],outline=color[i],width=4)
i=i+1
img.show()如下图:
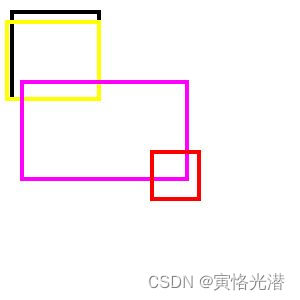
黑色框跟黄色框重叠部分很多,所以去掉黑色框,其余的粉红和红色框这些交并比很小,就属于其他类别的锚框了。
最后就是将这些方法一起运用到目标检测即可。新的一年祝大家有新的收获,由于本人水平有限,文章中有错误之处,还望指正!

![[Paper Reading] Towards Conversational Recommendation over Multi-Type Dialogs](https://cdn.jsdelivr.net/gh/xin007-kong/picture_new/img/20230122163613.png)