1247:河中跳房子
【题目描述】
每年奶牛们都要举办各种特殊版本的跳房子比赛,包括在河里从一个岩石跳到另一个岩石。这项激动人心的活动在一条长长的笔直河道中进行,在起点和离起点L远 (1 ≤ L≤ 1,000,000,000) 的终点处均有一个岩石。在起点和终点之间,有N (0 ≤ N ≤ 50,000) 个岩石,每个岩石与起点的距离分别为Di (0 < Di < L)。
在比赛过程中,奶牛轮流从起点出发,尝试到达终点,每一步只能从一个岩石跳到另一个岩石。当然,实力不济的奶牛是没有办法完成目标的。
农夫约翰为他的奶牛们感到自豪并且年年都观看了这项比赛。但随着时间的推移,看着其他农夫的胆小奶牛们在相距很近的岩石之间缓慢前行,他感到非常厌烦。他计划移走一些岩石,使得从起点到终点的过程中,最短的跳跃距离最长。他可以移走除起点和终点外的至多M (0 ≤ M ≤ N) 个岩石。
请帮助约翰确定移走这些岩石后,最长可能的最短跳跃距离是多少?
【输入】
第一行包含三个整数L, N, M,相邻两个整数之间用单个空格隔开。
接下来N行,每行一个整数,表示每个岩石与起点的距离。岩石按与起点距离从近到远给出,且不会有两个岩石出现在同一个位置。
【输出】
一个整数,最长可能的最短跳跃距离。
【输入样例】
25 5 2
2
11
14
17
21
【输出样例】
4
【提示】
在移除位于2和14的两个岩石之后,最短跳跃距离为4(从17到21或从21到25)。
思路
问题:将长度为L的线段中有N个点,移除M个点,留下N-M个点,将整条线段划分为N-M+1个线段。求所有可能的划分方案中,最短线段最长的那种方案下,最短线段的长度。
方案数有 种,N达到5 ∗ 10^ 4数量级,如果想枚举所有方案,求每种方案下的最短线段然后求最大值,显然不可行。
种,N达到5 ∗ 10^ 4数量级,如果想枚举所有方案,求每种方案下的最短线段然后求最大值,显然不可行。
逆向思考,如果给定点之间最小距离为x,即点之间的距离必须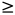 x。
x。
需要满足条件为:看移除M个点的多种方案中,是否存在一种方案其最短线段长度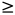 x
x
而要判断该条件是否成立,仍然比较困难。我们可以再逆向思考该命题,将其转化为:让每条线段长度都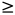 x,看最少需要移除多少个点。
x,看最少需要移除多少个点。
如果移除的点的数量小于等于M,则存在一种方案其最短线段长度
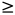 x,条件成立。
x,条件成立。
如果移除的点的数量大于M,则不存在这样的方案,条件不成立。
清楚要判断的条件后,这就是一个二分答案求满足某一条件最大值的问题
求中点:mid = (l + r)/2;
如果x满足条件,下一次x应该更大,取右半边,l = mid + 1;
如果x不满足条件,下一次x应该更小,取左半边,r = mid - 1;
最后得到的结果就是要求的各种方案中最短线段的最大值。
需要注意在进行当前枚举的最短距离判断时,不能直接用a[i] - a[i - 1]进行判断,因为a[i - 1]可能就已经被移走了,所以要用一个变量去保存上一块石头的距离,当某块石头没被移走,就更新下t作为新的距离值;

代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
int l,n,m,a[10000001];
bool check(int x)
{
int t = 0,num = 0;//t:当前观察的点的位置
for(int i = 1; i <= n; i++)
if(a[i] - t < x) num++;
else t = a[i];//如果点i到当前观察的位置的距离大于等于x则i的位置为当前观察的位置
if(l - t < x) num++;)//如果终点到观察点距离小于x则移除观察点
return num <= m;//看移除点的数量是否小于等于M
}
signed main()
{
cin>>l>>n>>m;
for(int i = 1; i <= n; i++) cin>>a[i];
int le = 0,ri = l,mid;
while(le + 1 < ri)
{
mid = (le + ri) / 2;
if(check(mid))
{
le = mid;
}
else
{
ri = mid;
}
}
cout<<le;
return 0;
}