详解动态规划01背包问题--JavaScript实现

对其他动态规划问题感兴趣的，也可以查看

详解动态规划最少硬币找零问题--JavaScript实现

详解动态规划最长公共子序列--JavaScript实现

一开始在接触动态规划的时候，可能会云里雾里，似乎能理解思路，但是又无法准确地表述或者把代码写出来。本篇将一步一步通过作图的方式帮助初次接触动态规划的同学来理解问题。这一篇将以经典的 01背包问题为例子来讲解，最后通过纯 JavaScript 来实现，在 Sublime 上运行演示。当然如果不会 JavaScript 也一点关系都没有，因为最重要的是理解整个推导过程。在语言实现的时候，也没有涉及什么语言特性，基本上懂个C语言就能看懂了。

问题

给定一个固定大小的背包，背包的容量为 capacity，有一组物品，存在对应的价值和重量，要求找出一个最佳的解决方案，使得装入背包的物品总重量不超过背包容量 capacity，而且总价值最大。本题中给出了3个物品，其价值和重量分别是 (3,2),(4,3),(5,4)。括号左边为价值，右边为重量，背包容量 capacity 为5。那么求出其搭配组合，使得背包内总价最大，且最大价值为多少？

分析

在开始计算之前，需要先对动态规划中的01背包问题有基本的理解：

物品无法拆成分数形式，如果能拆分，那就属于贪婪算法问题，在后面的文章我们也会介绍贪婪算法。

不一定恰好装满背包。

装满时总价值不一定最大。

每样物品各一件

常规情况下，在表格中，价格和重量一般都是从上到下递增的。我们填表分析的时候，其实是事先默认了这种递增的关系。

清楚了上面的原则之后，就可以开始进行分析了。

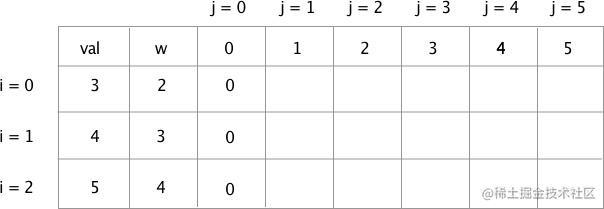
当一个新物品出现的时候，需要去决策如果选择了它，是否会让总价值最大化。我们根据问题，建立如下表格用于分析：

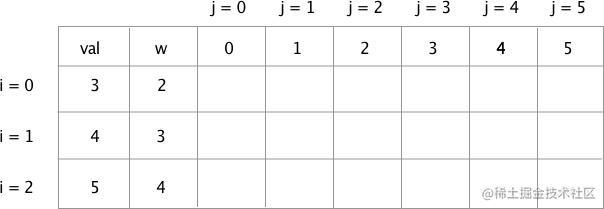
我们对这个表格做一下说明，左上角 val 和 w 分别是物品的价值和重量。即上面所描述的3个物品的价值与重量对应关系。

从第三列到最后一列，使用了变量 j，它表示背包总容量，最大值为5，也就是前面问题所说的 capacity 的值。

第二行到最后一行，使用 i 表示，下标从0开始，一共有3个物品，所以 i 的最大值为 2。即我们使用i表示物品，在下面介绍中将i=0称为物品0，i=1称为物品1，以此类推。

除了 j = 0 的情况以外，我们将从左到右，从上到下一步一步去填写这个表格，来找到最大的价值。

表格中未填写的空格，表示背包内物品总价值。我们后面将使用 T[i][j] 二维数组来表示它。

1. 总容量为0的情况

如果背包总容量为0，那么很显然地，任何物品都无法装进背包，那么背包内总价值必然是0。所以第一步先填满 j=0 的情况。

2. 第0行，i = 0 的空格分析

正如上面所说，我们接下来将从上到下，从左往右地填写这个表格。所以现在把注意力定位到 i =0, j = 1 的空格上。

在分析过程中，有一个重要原则：分析第i行时，它的物品组合仅能是小于等于i的情况。

怎么理解这个原则：比如分析i=0这一行,那么背包里只能装入物品0，不能装入其他物品。分析i=1这一行，物品组合可以是物品0和物品1

i=0 j=1 : 背包总容量为1，但是物品0 的重量为 2，无法装下去，所以这一格应该填 0。

i=0 j=2 : 背包总容量为2，刚好可以装下物品0 ，由于物品0 的价值为3，因此这一格填 3。

i=0 j=3 : 背包总容量为3，由于根据上面说明的物品组合原则，第0行，仅能放物品0，不需要考虑物品1 和物品2，所以这一格填 3。

i=0 j=4 : 同理，填 3 。

i=0 j=5 : 同理，填 3 。

这样我们可以完成第0行的填写，如下图：

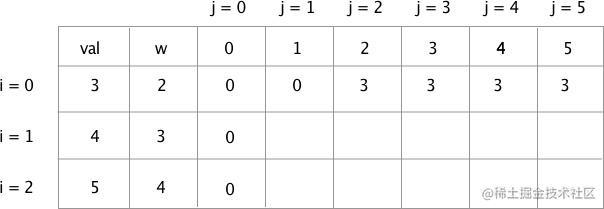
3. 第1行，i = 1 的空格分析

在这一行，可以由物品0 和物品1 进行自由组合，来装入背包。i=1 j=1 : 背包总容量为1，但是物品0 的重量为 2，物品1重量为3，背包无法装下任何物品，所以填 0。

i=1 j=2 : 背包总容量为2，只能装下物品0，所以填 3。

i=1 j=3 : 背包总容量为3，这时候可以装下一个物品1，或者一个物品0，仅仅从人工填表的方式，很容易理解要选择物品1，但是我们该如何以一个确切的逻辑来表达，让计算机明白呢？基于上面说说明的价值和重量在表格中从上到下递增原则，可以确认物品1的价值是大于物品0的，所以默认情况下优先考虑物品1，当选择了物品1之后，把背包剩余的容量和物品1之前的物品重量对比（也就是和物品0的重量对比，如果剩余重量能装下前面的物品，那么就继续装）。所以这里选择物品1，填 4

i=1 j=4 : 选择了物品1之后，物品1 的重量为3，背包容量为4，减去物品1的重量后，剩余容量为1，无法装下物品0，所以这里填 4

i=1 j=5 选择了物品1之后，剩余的容量为2，刚好可以装下物品0，所以一格背包装了物品1，和物品 0，总价值为7，把 7 填入表格。

这样我们就完成了第二行的填写，如下图：

3. 第2行，i = 2 的空格分析

i=2 j=1 : 填 0 。

i=2 j=2 : 填写这一行时，3种物品都有机会被装入背包。总容量为2时，只能装物品0，所以填 3。

i=2 j=3 : 物品2的重量为4，大于容量j，所以这里可以参考 T[i-1][j]的值，也就是 i=1 j=3那一格的值，填 4。

i=2 j=4 : 可以装下物品2，价值为5。也可以装下物品1。这一空格需要谨慎一点。我们将使用更严谨的方式来分析。在i=1 j=5 中出现了物品组合一起装入背包的情况，这一空将延续这种分析方式。我们选择了物品2，剩余的容量表达式应为 j-w[i] 即 4 - 4 = 0，剩余的容量用于上一行的搜索，由于上一行我们是填写完的，所以可以很轻易地得到这个值。表达式可以写成 val[i] + T[i-1][j-w[i]] ，可以根据这个表达式得出一个值。但是这并不是最终结果，还需要和上一行同一列数值对比，即 T[i-1][j]，对比，取最大值。最后这里填 5。

i=2 j=5 : 根据上面计算原理，这里如果选择了物品2，那么最大价值只能5，参照上一行，同一列，价值为7，取最大值。所以放弃物品2，选择将物品0和物品1装入背包，填写7。

完成后的表格如下：

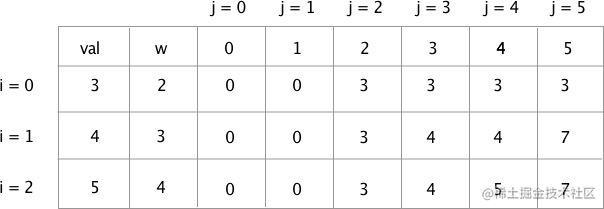
伪代码表达

理解了上面整个填表过程，我们要把逻辑抽取出来，在具体代码实现之前，先用伪代码表达出来。

if(j < w[i]){ //容量小于重量，hold不住
	T[i][j] = T[i-1][j]; //所以值等于上一行，同一列。如果i=0,没有上一行，则T[i][j] 取0
}else{
	T[i][j] = max(val[i] + T[i-1][j-w[i]] , T[i-1][j]);  //参照上面 i=2 j=4 和 i=2 j=5 时的填表分析
}
复制代码

以上这简短的伪代码就是解决问题的核心思路，可以应用于任何你熟悉的编程语言上。

说到这里，这篇文章应该是要基本告一段落了。

JavaScript 实现

如果你已经理解了上面的填表分析和伪代码表达，那么就可以尝试着自己去用代码实现了。最后放出在使用 JavaScript的一种实现方式供大家参考，不再针对针对代码做太多说明，重要区域会有注释。如果 Sublime 支持纯 JavaScript，可以直接复制黏贴，command+b 运行看结果。

function knapSack(w,val,capacity,n){
    var T = []

    for(let i = 0;i < n;i++){
        T[i] = [];
        for(let j=0;j <= capacity;j++){
            if(j === 0){ //容量为0
                T[i][j] = 0;
                continue;
            }    
            if(j < w[i]){ //容量小于物品重量，本行hold不住
                if(i === 0){
                    T[i][j] = 0; // i = 0时，不存在i-1，所以T[i][j]取0

                }else{
                    T[i][j] = T[i-1][j]; //容量小于物品重量，参照上一行

                }
                continue;
            }
            if(i === 0){
                T[i][j] = val[i]; //第0行，不存在 i-1, 最多只能放这一行的那一个物品
            }else{
                T[i][j] = Math.max(val[i] + T[i-1][j-w[i]],T[i-1][j]);

            }
        }

    }

    findValue(w,val,capacity,n,T);


    return T;
}


//找到需要的物品
function findValue(w,val,capacity,n,T){

    var i = n-1, j = capacity;
    while ( i > 0 && j > 0 ){

        if(T[i][j] != T[i-1][j]){

            console.log(i,j,'选择物品'+i+',重量：'+ w[i] +',价值：' + values[i]);
            j = j- w[i];
            i--;
        }else{
            i--;  //如果相等，那么就到 i-1 行
        }
    }
    if(i == 0 ){
        if(T[i][j] != 0){ //那么第一行的物品也可以取
            console.log(i,j,'选择物品'+i+',重量：'+ w[i] +',价值：' + values[i]);

        }
    }
}

// w = [2,3,4].  val = [3,4,5] , n = 3 , capacity = 5
//function knapSack([2,3,4],[3,4,5],5,3);
// 
var values = [3,4,5],
    weights = [2,3,4],
    capacity = 5,
    n = values.length;

console.log(JSON.stringify(knapSack(weights,values,capacity,n)));

结果：

D:\program\nodejs\node.exe .\src\test_math.js
1 5 选择物品1,重量：3,价值：4
src/test_math.js:45
0 2 选择物品0,重量：2,价值：3
src/test_math.js:54
[[0,0,3,3,3,3],[0,0,3,4,4,7],[0,0,3,4,5,7]]

改进方便理解：

function doDynamic(values,weights,capacity){
    let row = values.length;
    let arr = [];

    for (let i = 0; i < row; i++){
        arr[i] = [];
        for (let j = 0; j <= capacity; j++){
            if (j === 0){
                arr[i][j] = 0;
            }else{
                if (j < weights[i]){
                    if (i === 0){
                        arr[i][j] = 0;
                    }else {
                        arr[i][j] = arr[i-1][j]; 
                    }
                }else{
                    if (i === 0){
                        arr[i][j] = values[i];
                    }else{
                        arr[i][j] = Math.max(values[i] + arr[i-1][j-weights[i]],arr[i-1][j] );
                    }
                }
            }
        }
    }
    return arr;
}


let values = [3,4,5];
let weights = [2,3,4];
let capacity = 5;
let arr = doDynamic(values,weights,capacity);
console.log('v','w',JSON.stringify([0,1,2,3,4,5]));
arr.forEach((v,i)=>{
    console.log(values[i],weights[i],JSON.stringify(v));
})

结果：

v w [0,1,2,3,4,5]
3 2 [0,0,3,3,3,3]
4 3 [0,0,3,4,4,7]
5 4 [0,0,3,4,5,7]

参考：https://juejin.cn/post/6844903607855251463