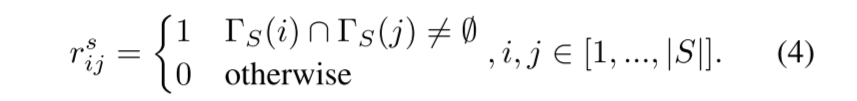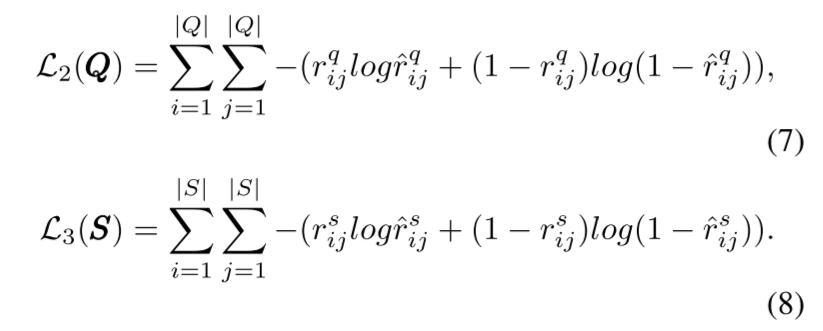摘要
知识追踪 (KT) 定义了根据学生的历史反应预测他们是否能正确回答问题的任务。尽管许多研究致力于利用问题信息,但问题和技能中的大量高级信息尚未被很好地提取,这使得以前的工作难以充分执行。在本文中,我们证明了通过在丰富的边信息上为每个问题预训练嵌入,然后在获得的嵌入上训练深度 KT 模型,可以实现 KT 的巨大收益。具体而言,边信息包括问题难度和问题与技能二分图中包含的三种关系。为了预训练问题嵌入,我们建议使用基于产品的神经网络来恢复边信息。因此,在现有深度 KT 模型中采用预训练嵌入在三个常见的 KT 数据集上都显然优于最先进的基线。
介绍
计算机辅助教育 (CAE) 系统正在寻求使用先进的基于计算机的技术来提高学生的学习能力和教师的教学效率。知识追踪 (KT) 是 CAE 系统中的一项基本任务,旨在根据学生的学习历史评估学生的知识状态。具体来说,KT的目标是根据之前的所有回答记录,预测学生能否正确回答下一题。
为了解决 KT 问题,已经提出了各种方法包括贝叶斯知识追踪 (BKT) ,因子分析模型和深度模型。在本文中,我们主要关注深度 KT 模型,它利用深度学习的最新进展并在 KT 方面取得了巨大成功。一般来说,大多数深度 KT 模型估计学生对技能的掌握程度,而不是直接预测她正确回答特定问题的能力。两种代表性方法是 DKT 和 DKVMN 。
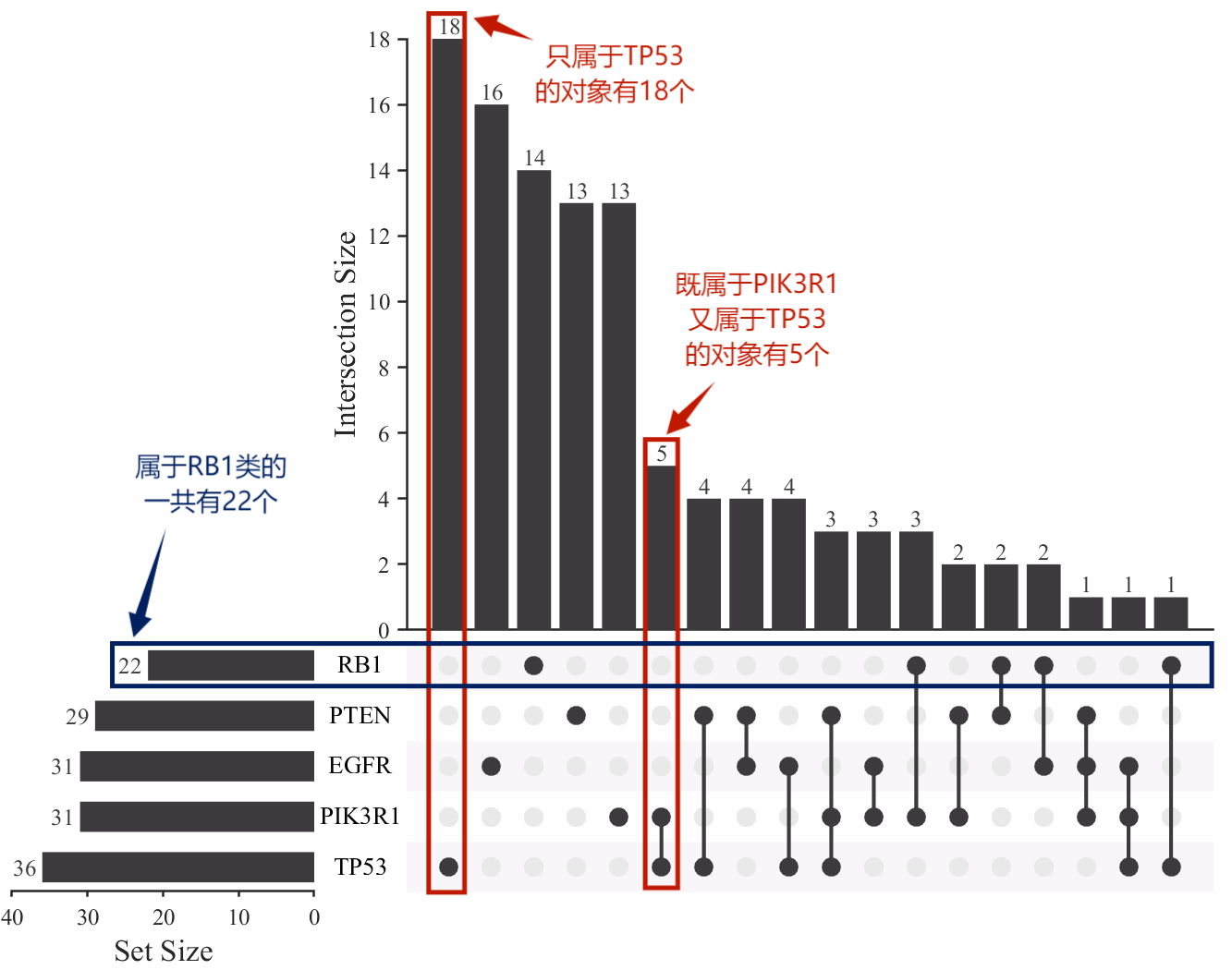
虽然这些深度 KT 模型可以很好地预测技能水平的掌握程度,但存在一个主要限制,即没有考虑特定问题的信息 。如图1所示,共享相同技能的问题可能有不同的难度,因此技能水平预测不能准确反映学生对特定问题的知识状态。尽管利用特定问题的信息在更细粒度的层面上解决 KT 是非常必要的,但存在一个主要问题,即学生与问题之间的交互极其稀疏,如果直接使用问题作为网络会导致灾难性的失败输入。为了解决稀疏性问题,提出了一些工作来使用问题信息作为补充 。然而,这些作品只考虑了问题的困难或问题与技能的关系。
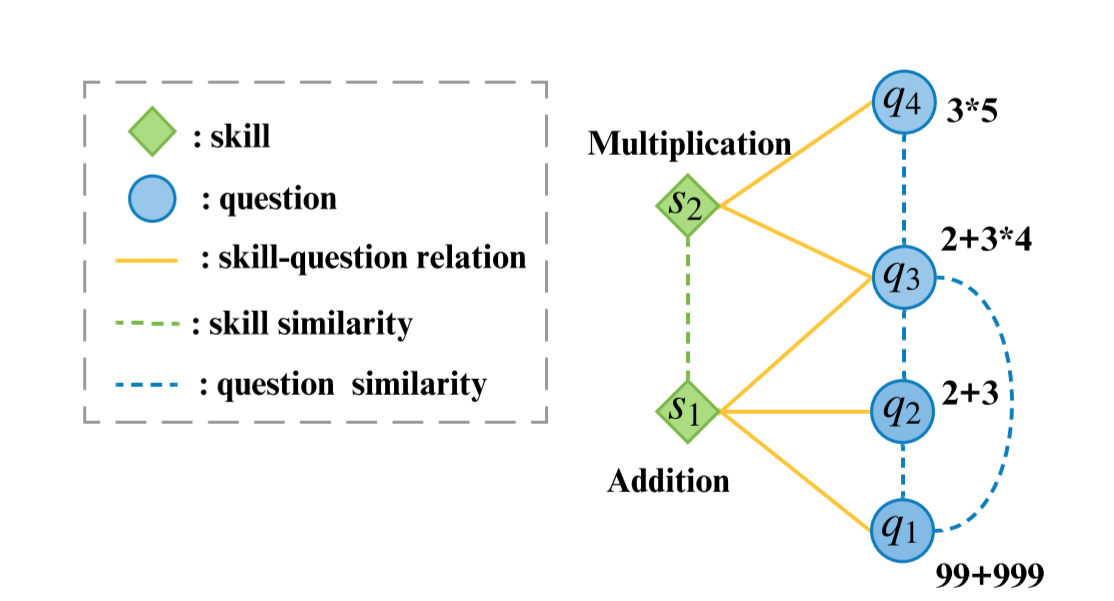
在本文中,我们朝着最大限度地提取和利用问题和技能之间的大量基础信息来解决稀疏性问题迈进了一步。考虑到通常一个技能包含很多问题,一个问题也与多个技能相关联,我们可以将它们表示为一个二分图,顶点分别是技能和问题。通常,二分图包括两种关系:显式关系(即观察到的链接)和隐式关系(即未观察到但可传递的链接)。在图 1 所示的 KT 场景中,除了明确的问题-技能关系外,我们还考虑了隐含的技能相似性和问题相似性,这在以前的工作中没有得到很好的利用。
考虑到所有因素,在本文中,我们提出了一种预训练方法,称为通过二分图 (PEBG) 进行的预训练嵌入,以使用所有有用的边信息为每个问题学习低维嵌入。具体来说,边信息包括问题难度和三种关系:显式的问题-技能关系、隐式的问题相似性和技能相似性。为了有效地提取边信息中包含的知识,我们采用产品层来融合问题顶点特征、技能顶点特征和属性特征以产生我们最终的问题嵌入。这样,学习到的问题嵌入将保留问题难度信息以及问题和技能之间的关系。 本文的贡献总结如下:
- 就我们最好的情况而言,我们是第一个使用问题-技能关系的二分图来获取问题嵌入的人,它提供了丰富的关系信息。
- 我们提出了一种称为PEBG的预训练方法,该方法引入了一个产品层来融合所有输入特征,以获得最终的问题嵌入。
- PEBG获得的问题嵌入可以合并到现有的深度KT模型中。在三个真实数据集上的实验结果表明,使用PEBG可以优于最先进的模型, AUC 平均提高 8.6%。
相关工作
以前的 KT 方法可以大致分为三种类型:贝叶斯知识追踪 (BKT)、因子分析 KT 模型和深度 KT 模型。 提出了贝叶斯知识追踪 (BKT) 模型,该模型是一个隐马尔可夫模型,将学生的知识状态假设为一组二元变量。 BKT 分别对每个技能状态建模,使其无法捕捉技能之间的关系。 KT方法的另一条路线是因素分析,它考虑影响学生状态的因素,包括问题的难度,学生的能力,对某题的正确答案的比例。因子分析模型包括项目反应理论(IRT)、加性因子模型(AFM)、绩效因子分析(PFA) , 知识追踪机 (KTM)。这些模型只考虑了每个问题或技能的历史交互,也没有捕捉到问题和技能之间的关系。随着深度学习的兴起,许多深度模型被提出来解决 KT,其中大多数初步工作使用技能作为网络输入。例如,Piech提出了深度知识追踪 (DKT) 模型,该模型使用递归神经网络 (RNN) 对学生的学习过程进行建模。Zhang提出的动态键值记忆网络 (DKVMN) 使用键值记忆网络自动发现练习与其基础概念之间的关系,并跟踪每个概念状态。 PDKT-C 模型 手动标记技能之间的先决条件关系,但不适用于大规模数据。 GKT 模型随机构建技能相似图,并自动学习图的边权重以帮助预测。由于技能水平预测不能完全反映特定问题的知识状态,一些工作提出使用问题信息作为补充。例如,Huang将问题的文本描述编码为问题嵌入以捕获问题特征,但文本描述在实践中并不容易获取。 Minn计算错误答案的百分比作为问题难度来区分不同的问题。 DHKT 使用问题和技能之间的关系作为约束来训练问题嵌入,这些问题嵌入与技能嵌入一起用作 DKT 的输入。在本文中,我们主要关注如何为每个问题预训练一个低维嵌入,它可以直接用作网络输入。
问题表述
在知识追踪中,给定学生过去的问题交互 X = {(q1, c1), …, (qt−1, ct−1)}, 其中 ci 是学生在时间步骤 i 时对问题 qi 的回答的正确性,目标是预测学生正确回答新问题的概率,即 P(ct = 1|qt, X)。
Q = {qi}|Q| i=1 是所有不同 |Q| 的问题集合, S = {sj}|S| j=1 是所有不同 |S| 的技能集合。通常,一项技能包含许多问题,一个问题与多项技能相关。所以问题-技能关系可以自然地表示为二分图 G = (Q,S,R) , 其中 R = [rij] ∈ {0, 1}|Q|×|S|是二元邻接矩阵。如果问题qi和技能sj之间存在一条边,则rij = 1, 否则 rij = 0。这里我们介绍我们将用于在我们的模型中训练嵌入的信息,包括图中的信息和难度信息。
- 显式的问题-技能关系
给定问题-技能二部图,技能顶点和问题顶点之间的关系是显式关系,取决于rij是否=1。 - 隐式的问题相似性和技能相似性
给定问题-技能二分图,具有共同问题顶点的邻居的两个技能顶点之间的关系被定义为技能相似性。类似地,问题相似性是指有共同技能顶点的邻居的两个问题顶点之间的关系。 - 问题难度
一个问题 qi 的问题难度 di 被定义为从训练数据集中计算出的正确回答的比率。所有的问题难度形成一个矢量 d = [di] ∈ R|Q|。
方法
在本节中,我们将详细介绍我们的 PEBG 框架,图 2 给出了其中的概述架构。PEBG使用四个损失函数对问题嵌入进行预训练,分别针对侧面信息设计:显式的技能-问题关系、隐式的问题相似性和技能相似性以及问题难度。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8UJGT76o-1674369196464)(D:\Photos\markdown\image-20230121144326071.png)]](https://img-blog.csdnimg.cn/a98b939e742b4ea7ae0a8c37715bacda.png)
输入特征
为了预训练问题嵌入,我们使用以下三种特征。需要注意的是,顶点特征是随机初始化的,会在预训练阶段进行更新,相当于学习从one-hot encodings到连续特征的线性映射。
- 技能顶点特征用特征矩阵表示 S ∈ R(|S|×dv) ,其中 dv 是特征的维度。对于一个技能si,顶点特征表示为si,它是矩阵S的第i行。
- 问题顶点特征由特征矩阵 Q∈R(|Q|×dv) 表示,其维度dv与技能顶点特征。对于一个问题qj,顶点特征表示为qj,即矩阵Q的第j行。
- 属性特征是与问题难度相关的特征,例如平均响应时间、问题类型等。对于问题 qi,我们将特征连接为 fi = [fi1; … ;fim], m是特征的数量。如果第 j 个特征是分类的 (例如,问题类型),则 fij 是一个
one-hot向量。如果第 j 个特征是数值的(例如,平均响应时间),则 fij 是一个标量值。
二分图约束
技能和问题顶点特征通过二分图约束更新。由于图中存在不同的关系,我们设计了不同类型的约束,以便顶点特征可以保留这些关系。
显式的问题-技能关系
在问题-技能二分图中,边存在于问题顶点和技能顶点之间,表示一个显式信号。类似于 LINE 中的一阶邻近度建模,我们通过考虑技能和问题顶点之间的局部邻近度来建模显式关系。具体来说,我们使用内积来估计嵌入空间中问题和技能顶点之间的局部接近度
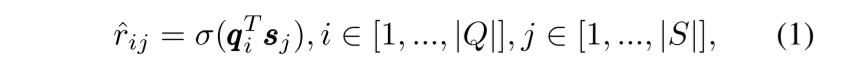
其中 σ(x) = 1/(1 + e^−x) 是 sigmoid 函数,它将关系值转换为概率。
为了保持显式关系,局部邻近性通过(最小化)交叉熵损失函数来接近二分图中的技能-问题关系:
已经计算出 ^rij 通过最小化L1(Q, S)的值, 从而确定 rij 的值, 即问题-技能矩阵
隐式相似性
PEBG 中使用的隐式相似性表示二分图中邻域之间的相似性。具体来说,存在两种相似性:技能相似性和问题相似性。我们希望同时使用隐式相似性来更新顶点特征。我们将问题qi的邻居集定义为ΓQ(i) = {sj|rij = 1},技能 sj 的邻居集为 ΓS(j) = {qi|rij = 1}。则问题相似性矩阵 RQ = [rq ij] ∈ {0, 1} ^ (|Q|×|Q|) 可以正式定义为:
类似地,我们定义技能相似性矩阵 RS = [rs ij]∈{0, 1}|S|×|S|为:
我们还使用内积来估计顶点特征空间中问题和技能各自的隐式关系:
问题难度约束
问题的难度信息在KT预测中很重要,但是二分图中却不包含。因此,我们希望最终的问题嵌入能够恢复难度信息。Vie 和 Kashima使用分解机对辅助信息进行编码并探索学生建模的特征交互。在本文中,我们使用与顶点特征交互的属性特征来学习高质量的嵌入。特别受PNN的启发 (一个用于学习高阶特征交互产品层)。
对于一个问题q (为清楚起见省略其下标),我们有它的问题顶点特征 q 和它的属性特征 f。为了通过产品图将属性特征与顶点特征进行交互,我们首先使用由 wa 参数化的线性层将属性特征 f 映射到低维特征表示,表示为a∈Rdv。假设与 q 相关的技能集是 C = {sj}^|C| j=1,我们用C中所有技能顶点特征的平均值表示作为 q 的相关技能特征,记为s’。在数学上有:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ciOtTLgu-1674369196470)(D:\Photos\markdown\image-20230121151629093.png)]](https://img-blog.csdnimg.cn/e8c113a91fde44299de3ca269ab9b0c1.png)
我们使用顶点特征q、平均技能特征s’, 和属性特征a生成问题q的线性信息Z和二次信息P。具体说来:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-z8MjvQDU-1674369196470)(D:\Photos\markdown\image-20230121153005349.png)]](https://img-blog.csdnimg.cn/34fdeeb26bf6433396b4db3b3877e38a.png)
其中 pij = g(zi, zj) 定义了成对特征交互。g 有不同的实现。在本文中,我们将 g 定义为向量内积:g(zi, zj) =<zi, zj>。然后我们介绍一个产品层,它可以转换这两个信息矩阵为信号向量lz和lp,如图2所示。变换方程为遵循:
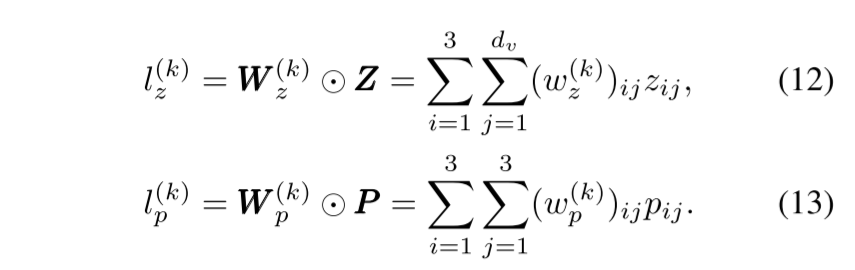
k ∈ [1, …d]。⊙表示首先对两个矩阵进行逐元素乘法运算,然后将乘法结果相加为一个标量。d 是 lz 和 lp 的变换维度。 W(k) z 和 W(k) p是产品层的权重。
根据P的定义和向量内积中的交换律,P和W(k) p应该是对称的,因此我们可以使用矩阵分解来降低复杂性。通过引入W(k) p = θ(k)θ(k)T 和 θ(k) ∈ R3 的假设,我们可以将 l(k) p 的表述简化为:
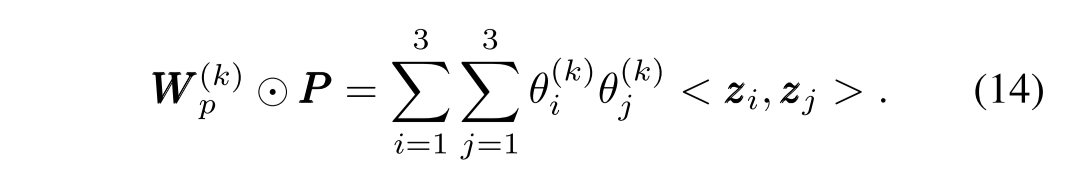
然后,我们可以计算问题 q 的嵌入,表示为 e:
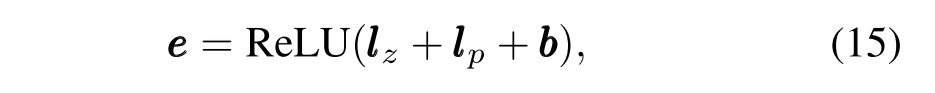
其中 lz, lp 和偏置矢量 b ∈ Rd,lz = [ l(1) z, l(2) z , …l(d) z],lp = [ l(1) p,l(2) p, … l(d) p]。激活函数是整流线性单位 (ReLU),定义为 ReLU(x) = max(0, x)。为了有效地保存难度信息,对于一个问题qi,我们使用线性层将激活ei映射到难度近似^di = (wd)T ei + bd,其中wd和bd是网络参数。我们以问题难度di为辅助目标,设计了以下损失函数L4来测量难度逼近误差:
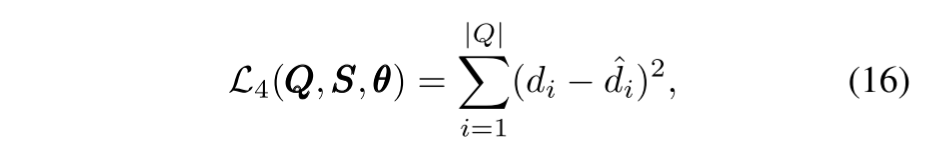
其中 θ 表示网络中的所有参数,即 θ = {wa, wz, wp, wd, b, bd}。
联合优化
为了生成同时保留显式关系、隐式相似性和问题难度信息的问题嵌入,我们将所有损失函数组合在一起形成一个联合优化框架,即求解:
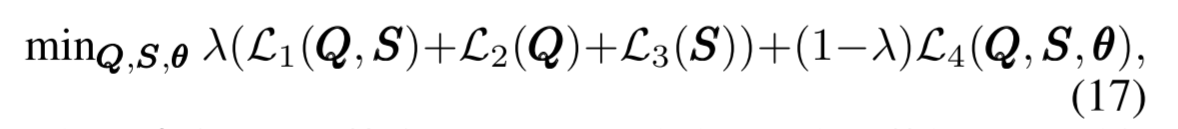
其中 λ 是控制二分图约束和难度约束之间权衡的系数。联合优化完成后,我们可以得到问题嵌入e,它可以作为现有深度 KT 模型的输入,例如 DKT 和 DKVMN。
结论
在本文中,我们提出了一种新的预训练模型PEBG,该模型首先将问题-技能关系表述为二分图,并引入产品层来学习用于知识追踪的低维问题嵌入。在真实数据集上的实验表明,PEBG显着提高了现有深度KT模型的性能。此外,可视化研究表明PEBG捕获问题嵌入的有效性,这为其高性能提供了直观的解释。
练模型PEBG,该模型首先将问题-技能关系表述为二分图,并引入产品层来学习用于知识追踪的低维问题嵌入。在真实数据集上的实验表明,PEBG显着提高了现有深度KT模型的性能。此外,可视化研究表明PEBG捕获问题嵌入的有效性,这为其高性能提供了直观的解释。
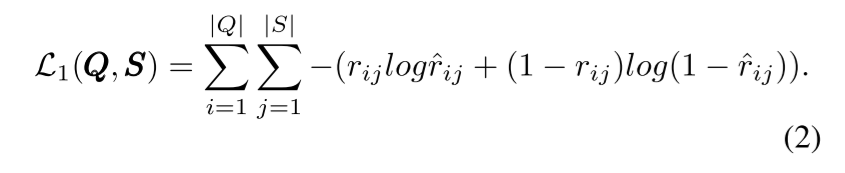
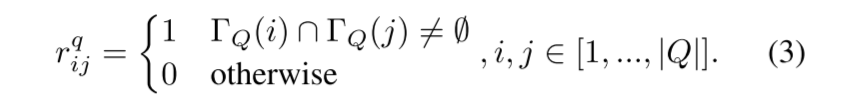
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tyGORe26-1674369196466)(D:\Photos\markdown\image-20230121143244829.png)]](https://img-blog.csdnimg.cn/00d7aeae15c846caae84e42d787ccee0.png)