各位CSDN的uu们你们好呀,欢迎来到小雅兰的课堂,今天我们的内容是复习之前的内容,并把之前的内容的一些习题一起来做一做,现在,就让我们进入二分查找的世界吧
首先,我们介绍的题目就是二分查找,也叫折半查找
我们定义了一个整型数组,为1 2 3 4 5 6 7 8 9 10,这个数组所有元素的下标为0 1 2 3 4 5 6 7 8 9,然后定义下标为0的元素为left,定义下标为9的元素为right,中间元素为mid

我们先假设要查找的元素就是7,那么就可以写出这样一个式子:mid=(left+right)/2;然后再进行二分查找,由下图可知,用二分查找的方式找到7这个元素最多只需要查找4次,这样的效率远比遍历的方法的效率要高

下面,我们来用代码来实现一下此功能吧
#include<stdio.h>
int main()
{
int arr[]={1,2,3,4,5,6,7,8,9,10};
//0,1,2,3,4,5,6,7,8,9
int k=7;//k是要查找的数字
int sz=sizeof(arr)/sizeof(arr[0]);
//折半查找(二分查找),前提是数组有序
int left=0;
int right=sz-1;
int flag=0;//一个标记变量
while(left<=right)
{
int mid=(left+right)/2;
if(arr[mid]<k)
{
left=mid+1;
}
else if(arr[mid]>k)
{
right=mid-1;
}
else
{
printf("找到了,下标是:%d\n",mid);
flag=1;
break;
}
}
if(flag==0)
{
printf("找不到\n");
}
return 0;
}然后,我们来运行一些此代码

写到这里,我们不禁会想起一个问题:如果这个数组非常非常大怎么办?
如果这个数组非常非常大,left和right非常大,left没有超出整型范围的最大值,right也没有超过整型范围的最大值,但left+right的和超出了整形范围的最大值,就会造成溢出现象,溢出之后的数据再除以2,就不是平均值了,所以mid=(left+right)/2这样的写法还是存在潜在风险
我们可以这样写:mid=left+(right-left)/2;
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int main()
{
int arr[] = { 1,2,3,4,5,6,7,8,9,10 };
//0,1,2,3,4,5,6,7,8,9
int k = 7;//k是要查找的数字
scanf("%d", &k);
int sz = sizeof(arr) / sizeof(arr[0]);
//折半查找(二分查找),前提是数组有序
int left = 0;
int right = sz - 1;
int flag = 0;//一个标记变量
while (left <= right)
{
int mid = left+(right-left) / 2;
if (arr[mid] < k)
{
left = mid + 1;
}
else if (arr[mid] > k)
{
right = mid - 1;
}
else
{
printf("找到了,下标是:%d\n", mid);
flag = 1;
break;
}
}
if (flag == 0)
{
printf("找不到\n");
}
return 0;
}最后的结果也是非常正确的

我们再来研究研究,前段时间我们学习了“函数”这一知识点,那我们也是可以封装一个函数来实现此代码的,那好吧,一起来实操一下
#include<stdio.h>
int binary_search(int arr[],int k,int sz)
{
int left=0;
int right=sz-1;
while(left<=right)
{
int mid=left+(right-left)/2;
if(arr[mid]>k)
{
right=mid-1;
}
else if(arr[mid]<k)
{
left=mid+1;
}
else
{
return mid;
}
}
return -1;
}
int main()
{
int arr[]={1,2,3,4,5,6,7,8,9,10};
int k=0;
scanf("%d",&k);
int sz=sizeof(arr)/sizeof(arr[0]);
//找到了就返回下标,找不到就返回-1
int ret=binary_search(arr,k,sz);
if(ret==-1)
{
printf("找不到\n");
}
else
{
printf("找到了,下标是:%d\n",ret);
}
return 0;
}好啦,用封装函数的方法也实现啦

那么,可能又会有人突发奇想,说:“可不可以把sz放在函数内部来求呢?”这个答案当然是否定的
它的代码是这个样子
#include<stdio.h>
int binary_search(int arr[], int k)
{
int left = 0;
int sz = sizeof(arr) / sizeof(arr[0]);
int right = sz - 1;
while (left <= right)
{
int mid = left + (right - left) / 2;
if (arr[mid] > k)
{
right = mid - 1;
}
else if (arr[mid] < k)
{
left = mid + 1;
}
else
{
return mid;
}
}
return -1;
}
int main()
{
int arr[] = { 1,2,3,4,5,6,7,8,9,10 };
int k = 0;
scanf("%d", &k);
//找到了就返回下标,找不到就返回-1
int ret = binary_search(arr, k);
if (ret == -1)
{
printf("找不到\n");
}
else
{
printf("找到了,下标是:%d\n", ret);
}
return 0;
}你运行起来,会发现,无论输入2之后的任意数字,输出的结果都是找不到

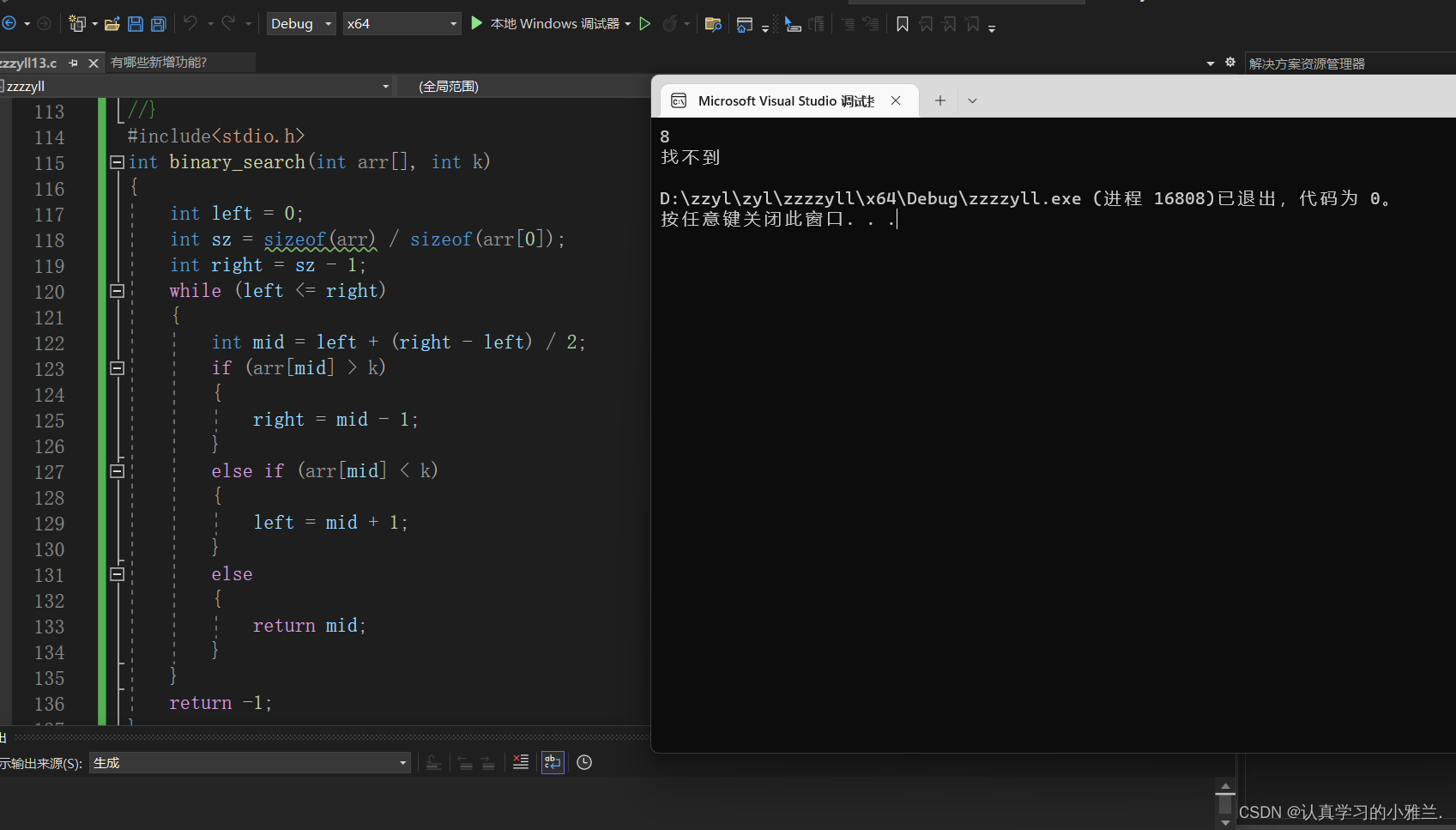
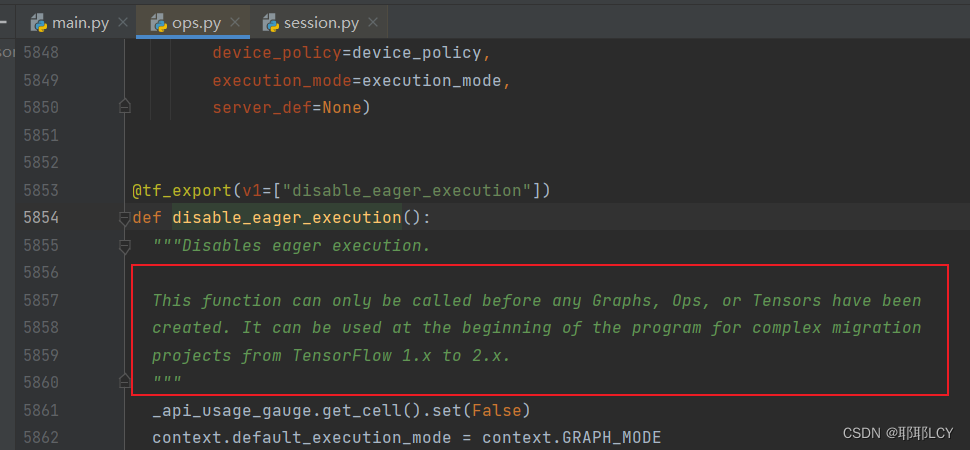
因为:arr是数组名,进行函数传参的时候,传进来的是首元素的地址,在binary_search()函数的形参中,arr实质上是一个指针,sizeof(arr)只是算出来这个首元素的地址所占空间大小,sizeof(arr[0])是这个元素占的空间大小,两者相除必为1.
而在主函数中求sz,sizeod(数组名) 计算的是整个数组的大小
sizeof内部单独放一个数组名,数组名表示整个数组
好啦,小雅兰今天的内容就到这里啦,今天的内容可能比较简单,也很少,但是小雅兰有认真在学噢!!!uu们加油呀



![[Linux]进程优先级 Linux中的环境变量](https://img-blog.csdnimg.cn/469c812073324c35bba0bfeb599d7f9c.png)