操纵运动学

在这里插入图片描述
ISAAC教程合集地址

文章目录

操纵运动学
- 应用架构
- 实施细节
- - 正向运动学
  - 逆运动学
- 小码

为了控制机器人手臂的运动，需要数学表示法来计算执行器输入并为轨迹规划器表示障碍物。为实现这一点，操纵运动学 GEM 将铰接式机器人系统表示为连接的刚体，并在配置空间和笛卡尔空间之间转换机器人状态。

应用架构

机器人手臂被建模为一棵链接树，每个链接都由一个字符串名称标识。每个链接都可以有一个“马达”来描述它的框架和它的子框架之间的转换。这种变换可以是恒定的（对于非关节链接和固定关节）或参数化用于可移动关节，如旋转关节。

注意

链接目前没有用于碰撞建模的关联几何体（网格）。

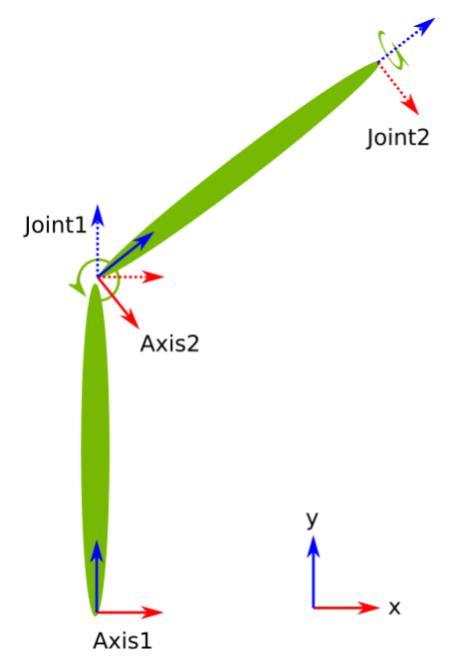
运动树的自由度是运动链中所有电机的自由度之和。下面的示例显示了具有四个链接的运动链。连杆“Axis1”和“Axis2”（实线框所示）具有恒定电机，连杆“Joint1”和“Joint2”（虚线框所示）具有参数化电机，旋转轴沿（001）和 (010)（在它们自己的帧中）分别。

实施细节

操纵运动学 GEM 位于 //engine/gems/kinematic_tree: kinematic_tree。所有计算都作为双四元数执行，以表示 3D 空间中的位移：有关更多详细信息，请参阅 //engine/core/math/dual_quaternion.hpp 组件。运动学状态的验证目前仅考虑关节限制；目前没有其他自碰撞检查。

正向运动学

为了从每个关节的位置找到末端执行器的位置，应用程序提取从根部到末端执行器的链接链，沿途乘以每个链接的对偶四元数。最终的对偶四元数将表示当前的 3D 位移并且可以转换为 Pose3d。

逆运动学

为了找到将末端执行器带到给定目标的关节配置，该应用程序使用雅可比转置实现了梯度下降法。对于过度指定的系统（即具有六个以上关节的系统），此解决方案提供与提供给求解器的初始状态最接近的配置。当目标状态和当前状态在配置步骤中连接和关闭时，以及当前状态作为初始猜测提供给求解器时，这是有效的。

小码

Manipulation Kinematics GEM 使用 KinematicTree codelet 加载运动学树文件，该文件的命名结构为“<name>.kinematic.json”。以下是文件格式的示例：

{
  "links": [
    {
      "name": "base",
      "motor": {
        "type": "constant",
        "properties": {
          "pose": {
            "translation": [0.0, 0.0, 0.0],
            "rotation": {
              "axis": [0.0, 0.0, 1.0],
              "angle_radians": 0.0
            }
          }
        }
      }
    },
    {
      "name" : "axis1",
      "parent": "base",
      "motor": {
        "type": "constant",
        "properties": {
          "pose": {
            "translation": [0.0, 0.0, 0.1373],
            "rotation": {
              "axis": [0.7071, 0.7071, 0.0],
              "angle_degrees": 180.0
            }
          }
        }
      }
    },
    {
      "name" : "joint1",
      "parent": "axis1",
      "motor": {
        "type": "revolute",
        "properties": {
          "axis": [0, 0, 1]
        }
      }
    }
  ]
}