一、本周周赛总结

• 大年初一，和昨晚一样出脑筋急转弯找规律，被自己笨哭。
• T1 模拟。
• T2 调库。
• T3 找规律。
• T4 序列DP。
  

二、 [Easy] 6296. 交替数字和

链接: 6296. 交替数字和

1. 题目描述

2. 思路分析

按题意模拟即可。

3. 代码实现

class Solution:
    def alternateDigitSum(self, n: int) -> int:
        ans = 0
        i = 1
        for c in str(n):
            ans += int(c)*i
            i *= -1
        return ans

三、[Medium] 6297. 根据第 K 场考试的分数排序

链接: 6297. 根据第 K 场考试的分数排序

1. 题目描述

2. 思路分析

题目这么长，但简单到不敢理解。

• 读完题犹豫半天才敢写。
• 写完犹豫半天才敢提交。

3. 代码实现

class Solution:
    def sortTheStudents(self, score: List[List[int]], k: int) -> List[List[int]]:
        score.sort(key=lambda x:x[k],reverse=True)
        return score

四、[Medium] 6298. 执行逐位运算使字符串相等

链接: 6298. 执行逐位运算使字符串相等

1. 题目描述

2. 思路分析

• 智商差距在这种题上就能体现，我wa一发之后不能理解暴wa的case于是去做T4了 ，回来再做T3。
• 手玩一下，由于i,j没有顺序，因此我们讨论任意两个数，可能的情况只有00,01,10,11,其中01和10可以看作一种。
• 按照规则：
  • 00只能变成00.
  • 11可以变10(01)
  • 01（10）可以变成11。
• 发现，s中只要有一个1，s就可以变成任意有1的情况。即只要s和target都有1，则一定可以变过去。如果任意一个有1，另一个没1，则变不过去。
• 如果没有1，只有0，那要求双方都是0。可以提前特判 s==target。

3. 代码实现

class Solution:
    def makeStringsEqual(self, s: str, target: str) -> bool:
        if s == target :
            return True 
        return '1' in s and '1' in target

五、[Hard] 6299. 拆分数组的最小代价

链接: 6299. 拆分数组的最小代价

1. 题目描述

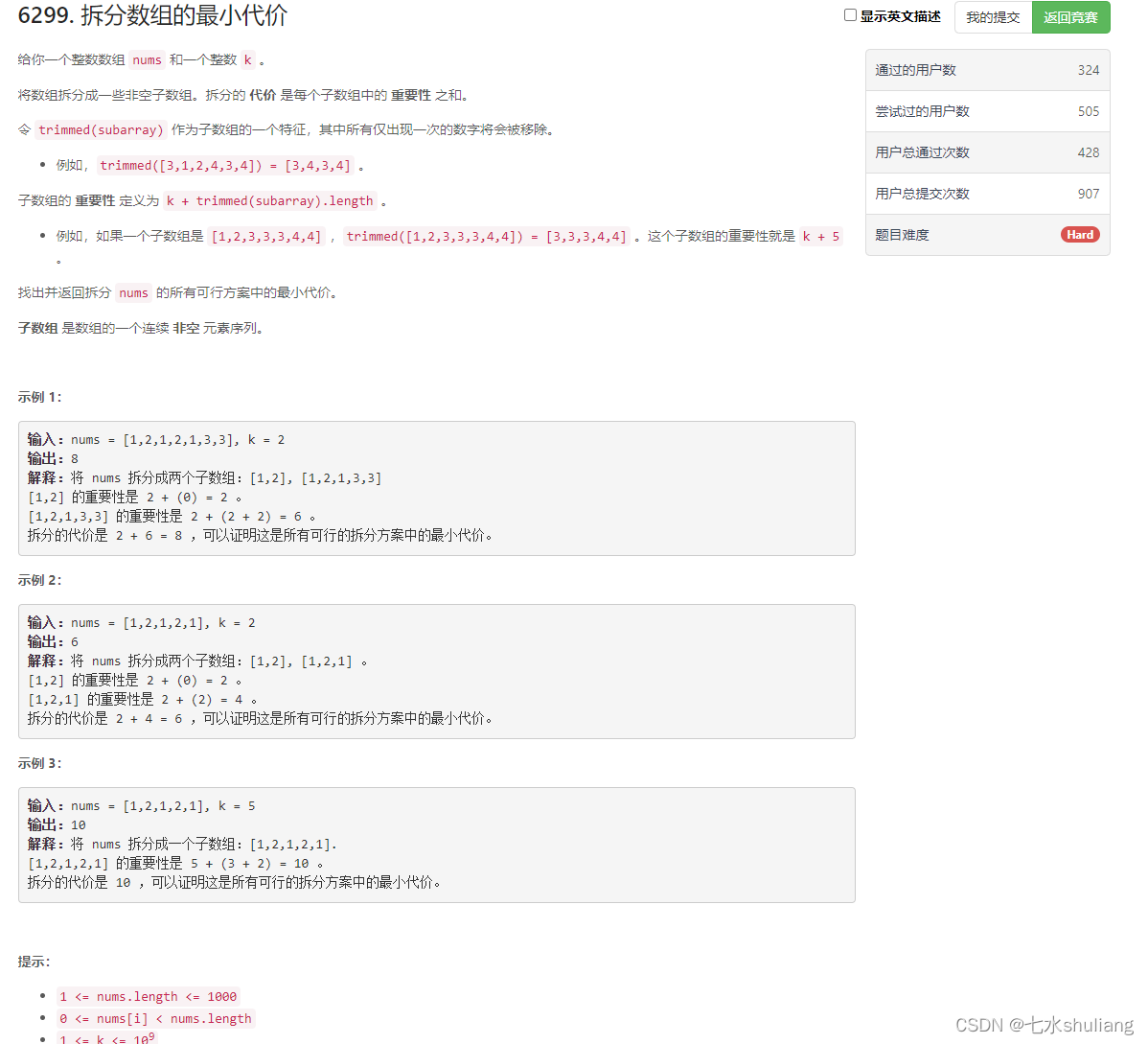
2. 思路分析

• 序列DP。
• 看到分割子数组，就要想到DP，讨论最后一个元素所在组的大小，不断往前延伸枚举答案。
• 看了下数据范围，正好是N方的，直接莽。
• 定义: f[i]为nums前缀i个数的最小代价.
• 初始: 显然一个数代价是k，分一组即可。f[0]=k。
• 转移: 讨论第i个数所在组的大小：
  • 自己一组: f[i] = f[i-1]+k
  • 和前边到j之前的一组:f[i] = f[j-1] + cost(a[j:i+1])
  • 取min即可。复杂度n方。
• 答案: f[-1]
• 实现时，把f向右偏移一位避免讨论下标0。可以理解为f[i]定义为前i个数的代价，f[i]=0。
• 转移时，需要计数每个数字，如果计数是1不增加代价，计数是2才开始增加。由于nums[i]<n可以用数组代替Counter，实测优化不多(py)。

3. 代码实现

class Solution:
    def minCost(self, nums: List[int], k: int) -> int:
        n = len(nums)
        f = [0] + [inf]*n       
        for i in range(n):
            f[i+1] = f[i]+k
            cnt = [0]*n
            cnt[nums[i]] += 1
            s = 0
            for j in range(i-1,-1,-1):
                v = nums[j]
                cnt[v] += 1
                if cnt[v] == 2:
                    s += 2
                elif cnt[v] > 2:
                    s += 1
                x = f[j]+k+s 
                if x < f[i+1]:
                    f[i+1] = x
        return f[-1]       

六、参考链接