史上最详细的AVL树的实现(万字+动图讲解旋转)

news2024/9/27 17:27:59

       🔥🔥 欢迎来到小林的博客！！
      🛰️博客主页：✈️小林爱敲代码
      🛰️文章专栏：✈️小林的C++之路
      🛰️欢迎关注：👍点赞🙌收藏✍️留言
首页图片

      AVL树是一个平衡二叉搜索，相比于红黑树，它更平衡。但是相比于插入删除的操作，红黑树更优。因为旋转有消耗，而红黑树的旋转明显要比AVL树少的多。所以这篇文章给大家带来了平衡二叉树的插入和查找操作，全程动图讲解！千万不要错过！至于删除操以后有机会为大家更新。


         每日一句: 即使道路坎坷不平，车轮也要前进；即使江河波涛汹涌，船只也航行。

目录

  • AVL树的概念
  • AVL树的节点创建
  • AVL类创建
  • AVL树的插入
  • 检查AVL树是否正常
  • 查找值
  • 总结🥳：

AVL树的概念

AVL是一颗平衡二叉搜索树，相比于二叉搜索树。AVL它能始终保持平衡，因为二叉搜索树的缺陷太大。当有序插入数据时，整颗树就会变成一个单链表。因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均
搜索长度。

AVL树需要满足以下两点性质:
1.它的左右子树都是AVL树。
2.每颗子树的高度差(平衡因子)不超过1或者小于-1。

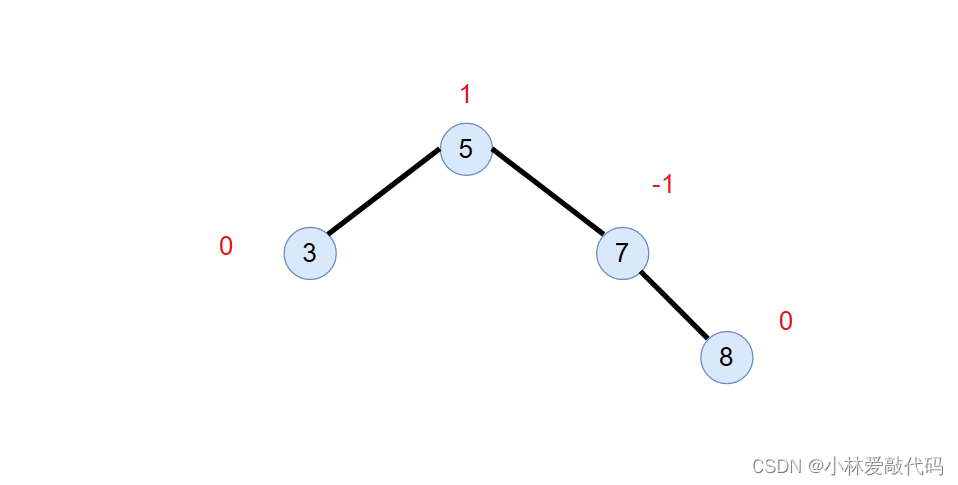
那我们来看看一颗典型的AVL树
在这里插入图片描述

我们可以发现，左边高，它的高度差就是 -1，右边高，高度差就是1。两边一样高，那么高度差就是 0 。所以我们可以用平衡因子，来确定它的一个高度差。这样可以更好的控制它的高度。

AVL树的节点创建

为了更好的控制，我们决定使用三叉链。也就是新增一个parent节点指向自己的父亲，根节点的父亲为空指针。而我们还要一个平衡因子变量，来记录它子树的高度差。left和right指针指向左右两个孩子。这里我们采取key,value模型，所以用pair结构体，作为节点的值。

节点结构体代码：

template<class K,class V>
struct AVLNode
{
	AVLNode<K, V>* _left;
	AVLNode<K, V>* _right;
	AVLNode<K, V>* _parent;
	int _bf; //平衡因子，记录高度差
	pair<K, V> _kv; //存储的一对数据
	//构造函数
	AVLNode(const pair<K,V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_bf(0) //新增节点肯定是叶子节点，所以高度默认0
		,_kv(kv){}
};

AVL类创建

只需要一个成员变量 root 来指向整颗树的根即可。构造函数就把root初始化为空。

	template <class K, class V>
	class AVLTree
	{
		typedef AVLNode<K, V> Node;
	public:
		AVLTree() :_root(nullptr){}
	private:
		Node* _root;//AVL树的根
	};

AVL树的插入

AVL树的插入，我们要先找到可以插入的位置，然后插入。插入之后我们树的高度可能会发生变化，因此我们需要向上去更新平衡因子。所以我们插入后分多种情况，那就是插入后平衡因子为 0, 1/-1 ，2/-2的情况

插入后平衡因子为0的情况：
插入后平衡因子为0，那么说明在插入之前，这颗树的平衡因子是 -1 或者1，所以在插入之后这棵树的平衡因子变成了0，那么就意味着这棵树已经平衡了，这种情况就不需要做什么事情了。
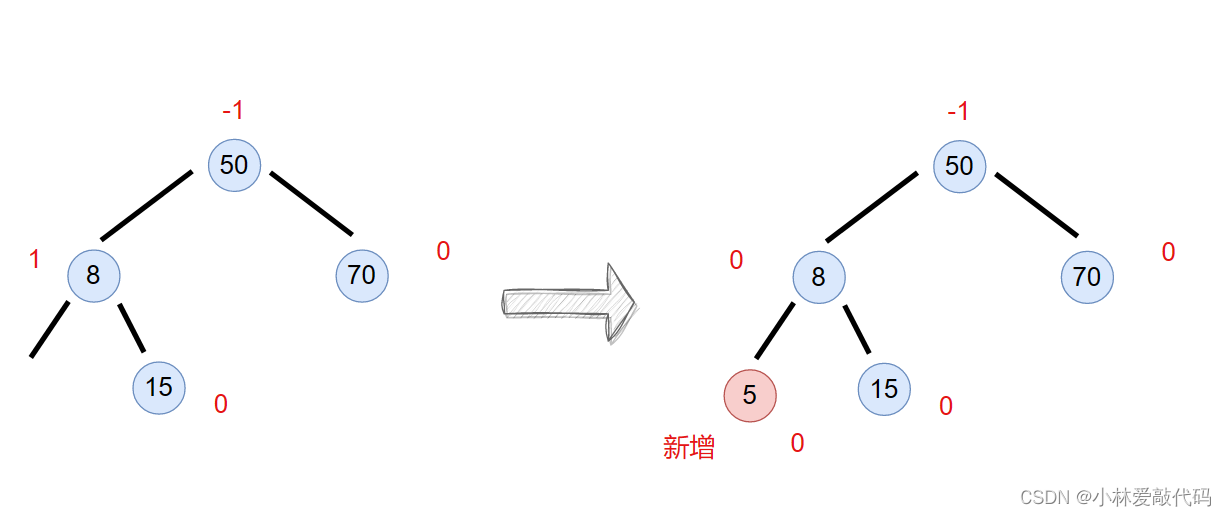
在这里插入图片描述


插入后平衡因子为1/-1的情况：
如果插入和平衡因子为1或者-1，说明在插入之前这棵树的平衡因子是0。也就是说插入之前这颗树是平衡的，而插入之后，引发了高度变化。所以可能会造成不平衡的情况，这种情况我们需要一种往上更新平衡因子。在更新的过程可能会遇到平衡因子变成 2 或者 -2的情况，这时候就需要发生旋转。

在这里插入图片描述


平衡因子为2/-2的情况：
在插入的过程中，平衡因子可能会出现为2/-2的情况。当平衡因子为1/-1的时候，会一直往上更新，而在更新的过程中就会发生平衡因子为 2/-2的情况，这种情况我们就需要发生旋转。

在这里插入图片描述

假设我们插入一个10，那么10插入的位置应该在 8的右边。
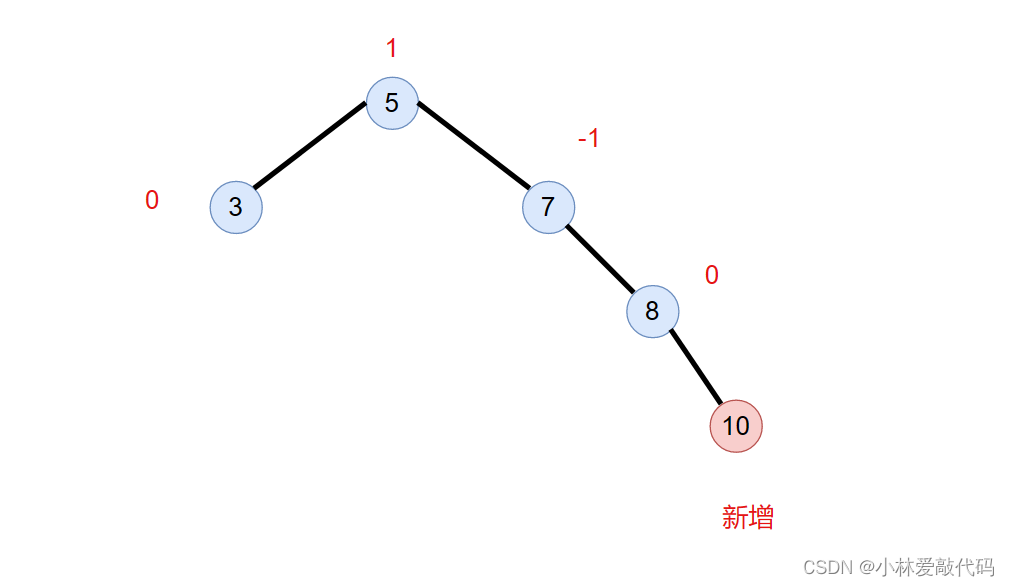
在这里插入图片描述
那么此时 8 的左右子树高度发生了变化，因为插入了一个新节点。如果新增节点在右边，则 平衡因子自减，如果新增节点在右边，则平衡因子自增。所以新增后，平衡因子的变化是。
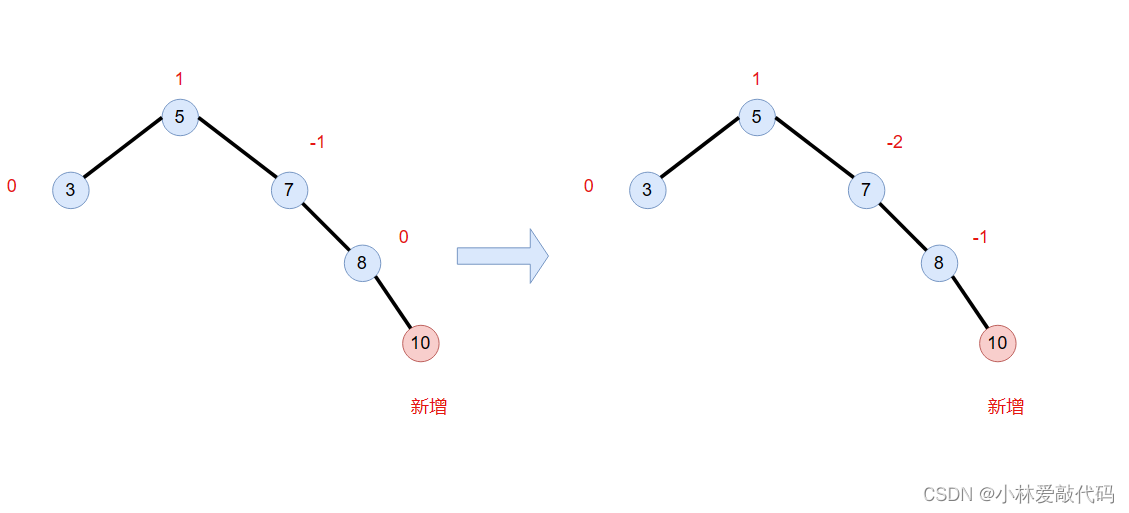
在这里插入图片描述
也就是，7所在的节点的子树不平衡了，因为它的平衡因子 > 1了。所以此时我们要发生旋转。而旋转有四种情况。


第一种情况，右边一边高

就如上图的情况，7所在节点的右子树右边一边高，所以这时候我们需要左旋转。那么我们假设7节点为parent。7的右节点8为subR，8的左节点为subRL，而7的父节点为parentparent
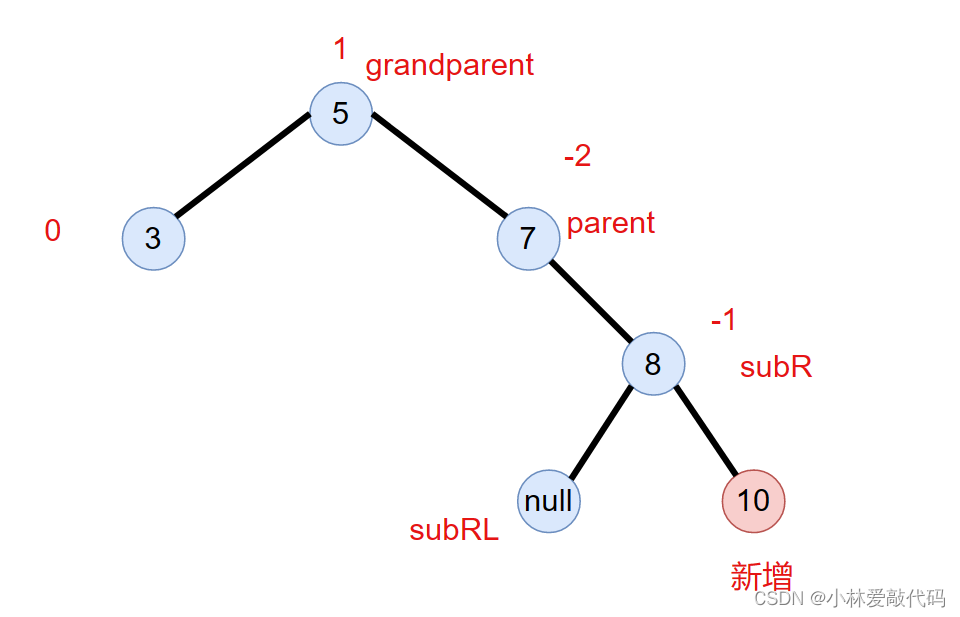
在这里插入图片描述

左单旋的步骤:
1.让parent的右节点连接subRL
2.subRL的父节点连接parent，如果为空则不连接
3.subR的左节点连接parent
4.parent的父节点连接subR
5.grandparent与subR连接

旋转流程图
在这里插入图片描述
最后，我们会发现parent和subR的平衡因子都变了0。也就意味着这颗子树达到了平衡。
左旋转代码：

		// 左单旋
		void RotateL(Node* parent)
		{
			Node* grandparent = parent->_parent;
			Node* subR = parent->_right;
			Node* subRL = subR->_left;
			//父亲连接subRL
			parent->_right = subRL;
			if (subRL)
				subRL->_parent = parent;

			//subR的左边连接parent
			subR->_left = parent;
			parent->_parent = subR;
			//grandparent连接subR
			if (grandparent == nullptr)
			{
				//grandparent为空，说明parent一开始是根节点
				_root = subR;
				subR->_parent = nullptr;
			}
			else
			{
				//如果parent一开是grandparent的左子树，则grandparent的左子树连接subR
				if (parent == grandparent->_left)
					grandparent->_left = subR;
				else
					grandparent->_right = subR;
				subR->_parent = grandparent;
			}
			//更新平衡因子
			parent->_bf = subR->_bf = 0;
		}




第二种情况：左边一边高
左边一边高和右边一边高的思路完全一样。只不过方向反过来。。下面这棵树就是左边一边高，所以我们用右单旋进行调整。
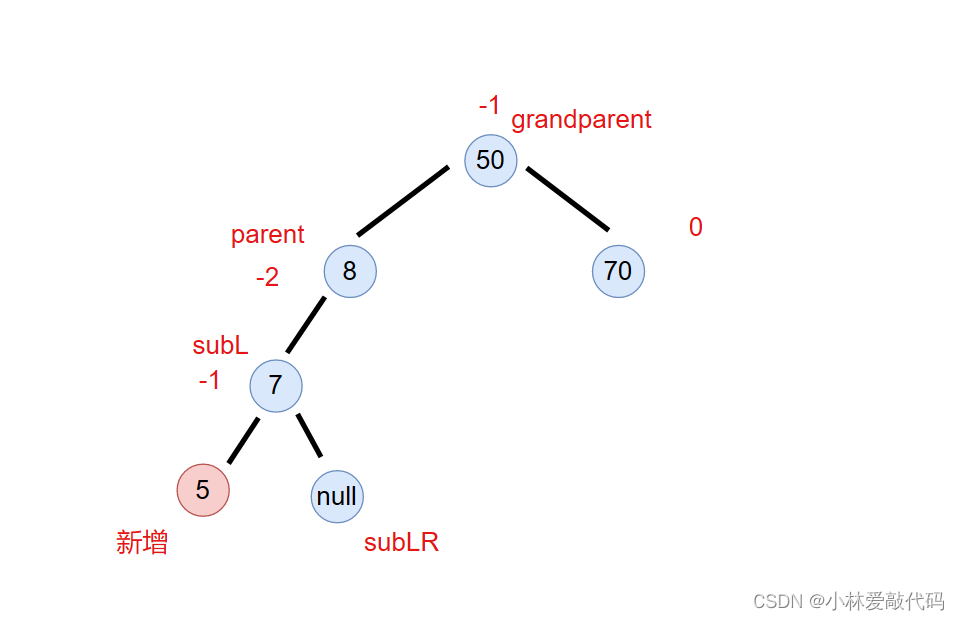
在这里插入图片描述

右单旋的步骤:
1.让parent的左节点连接subLR
2.subLR的父节点连接parent，如果为空则不连接
3.subL的右节点连接parent
4.parent的父节点连接subL
5.grandparent与subL连接

右单旋旋转动图:
在这里插入图片描述
右单旋代码：

		//右单旋
		void RotateR(Node* parent)
		{
			Node* subL = parent->_left;
			Node* subLR = subL->_right;
			Node* grandpraent = parent->_parent;
			parent->_left = subLR;
			if (subLR)
				subLR->_parent = parent;

			subL->_right = parent;
			parent->_parent = subL;
			if (grandpraent == nullptr)
			{
				_root = subL;
				subL->_parent = nullptr;
			}
			else
			{
				if (grandpraent->_left == parent)
					grandpraent->_left = subL;
				else
					grandpraent->_right = subL;
				subL->_parent = grandpraent;
			}
			subL->_bf = parent->_bf = 0;
		}

第三种情况：新节点插入较高左子树的右侧—左右
一边高是直线，曲线就是整棵树是左边高，但是它的孩子却在和它相反的一边。这就意味着这棵树是曲线的，所以单纯的左右旋转无法使它达到平衡。而旋转完后，我们还需要控制平衡因子，控制平衡因子又有三种情况。

情况1.当subL右节点的平衡因子为0时(也就是新增)
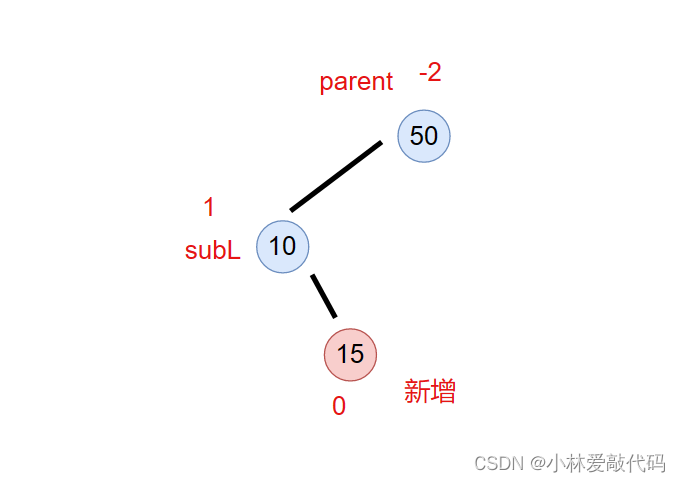
在这里插入图片描述

把subL左旋转后
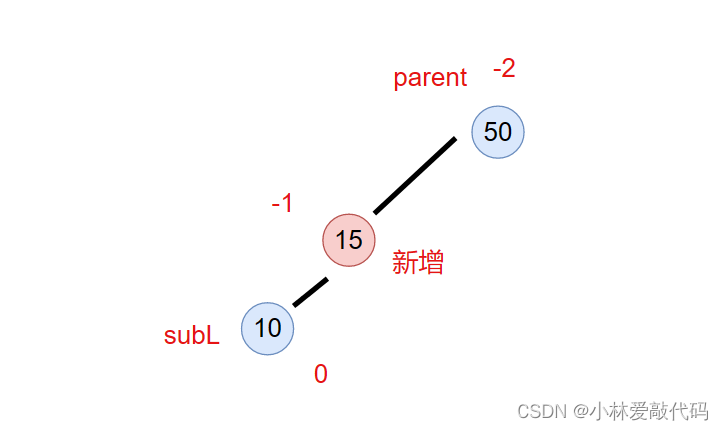
在这里插入图片描述

随后这颗树就变成了左边一边高，我们在把parent右旋转。
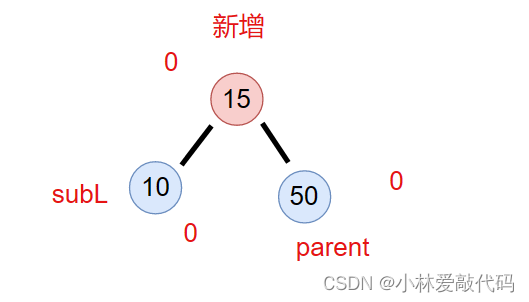
在这里插入图片描述

这种情况下，新增节点，subL，parent的平衡因子都变成了0。


情况2.subL的右节点平衡因子为-1时

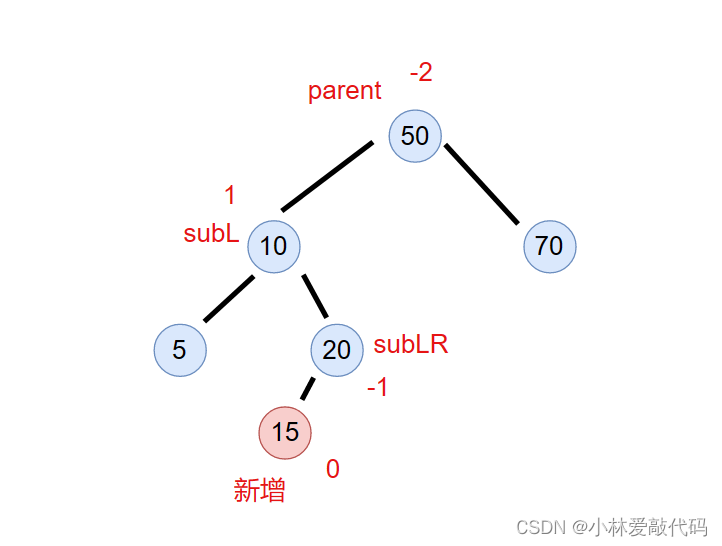
在这里插入图片描述

和之前一样，先把subL左旋转
在这里插入图片描述

再把parent右旋转
在这里插入图片描述

旋转后
subL的平衡因子为0
subLR的平衡因子为0
parent的平衡因子为1

情况3.subL的右节点平衡因子为1时
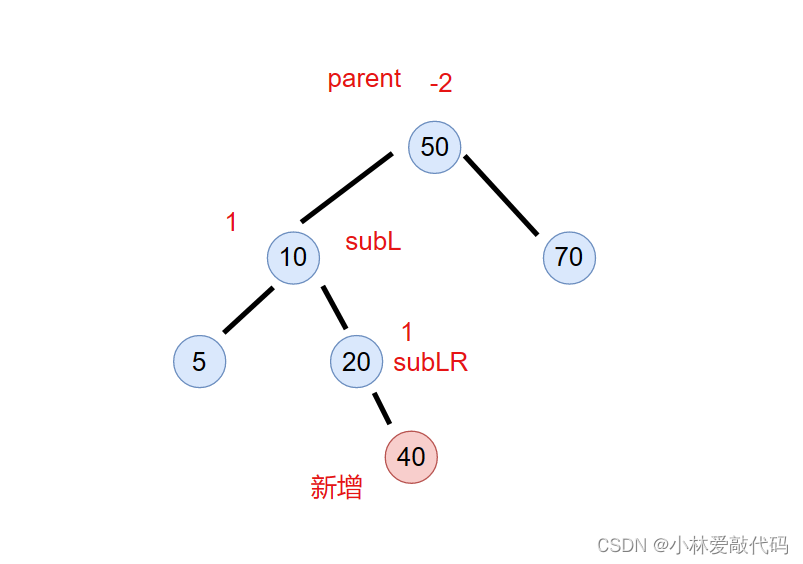
在这里插入图片描述

老规矩，把subL进行左单旋

在这里插入图片描述

再把parent右单旋
在这里插入图片描述

旋转后
subL的平衡因子为-1
subLR的平衡因子为0
parent的平衡因子为0

左右双旋代码:

	void RotateLR(Node* parent)
		{
			Node* subL = parent->_left;
			Node* subLR = subL->_right;
			int lrbf = subLR->_bf;

			//先左旋subL
			RotateL(subL);
			//右旋parent
			RotateR(parent);
			//保存LR的平衡因子
			if (lrbf == 0)
			{
				parent->_bf = subL->_bf = subLR->_bf = 0;
			}
			else if (lrbf == -1)
			{
				subL->_bf = subLR->_bf = 0;
				parent->_bf = 1;
			}
			else if (lrbf == 1)
			{
				subL->_bf = -1;
				subLR->_bf = parent->_bf = 0;
			}
			else
				assert(false);
		}

第四种情况：新节点插入较高左子树的左侧—右左
这种情况和第三种情况相反，但也另外分了三种情况。

情况1.subRL就是新增节点
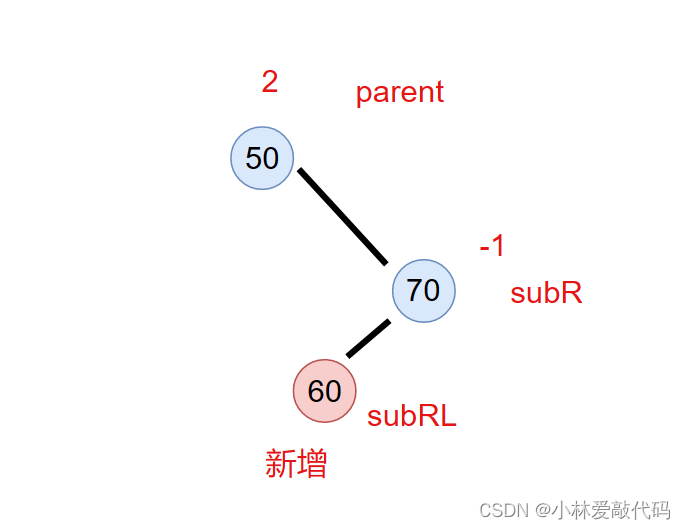
在这里插入图片描述

先右旋转subR
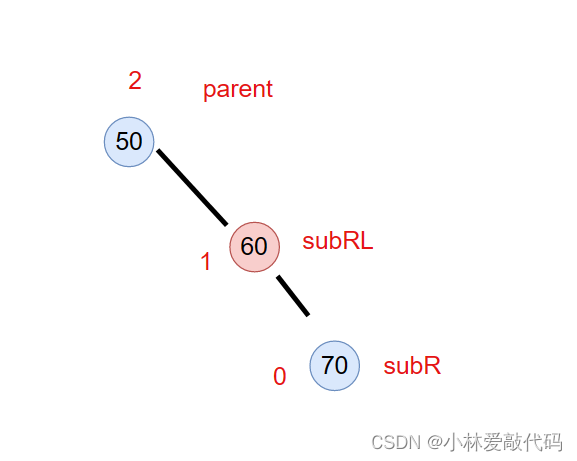
在这里插入图片描述
再左旋转parent
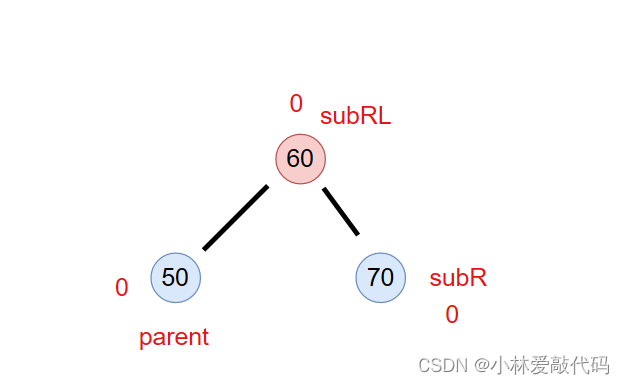
在这里插入图片描述
旋转完后，subRL和subR还有parent的平衡因子都为0。

情况2.当在subRL的平衡因子为-1时
在这里插入图片描述
先右单旋subR
在这里插入图片描述
再左单旋parent

在这里插入图片描述
最后的平衡因子分别为:
subRL 0
parent 0
subR 1

情况3.当在subRL的平衡因子为1时
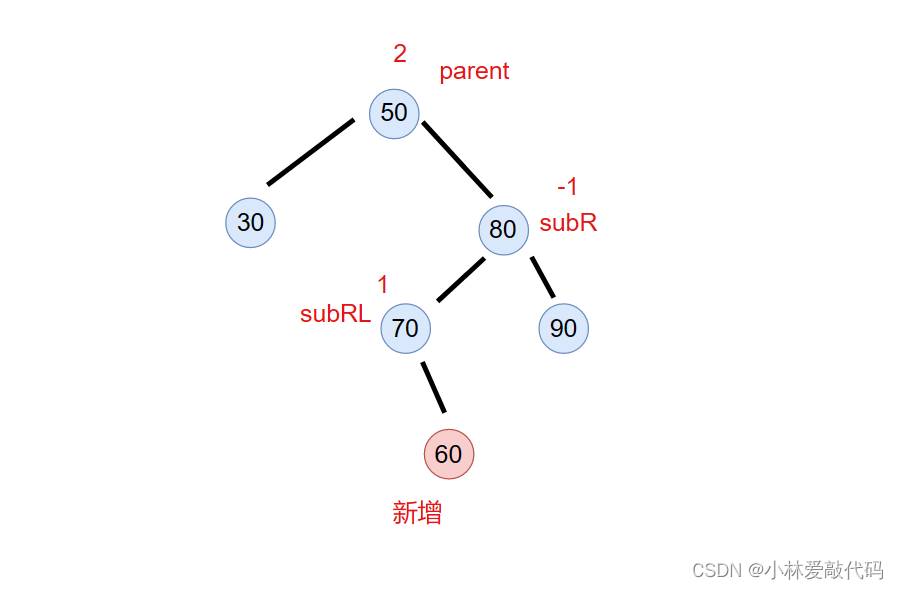
在这里插入图片描述
老规矩，先右旋 subR
在这里插入图片描述

然后左旋转parent
在这里插入图片描述
最后的平衡因子分别是：
parent -1
subRL 0
subR 0

右左双旋代码：

	//右左双旋
		void RotateRL(Node* parent)
		{
			Node* subR = parent->_right;
			Node* subRL = subR->_left;
			int rlbf = subRL->_bf;
			RotateR(subR);
			RotateL(parent);
			if (rlbf == 0)
			{
				subR->_bf = subRL->_bf = parent->_bf = 0;
			}
			else if (rlbf == -1)
			{
				subRL->_bf = parent->_bf = 0;
				subR->_bf = 1;
			}
			else if (rlbf == 1)
			{
				parent->_bf = -1;
				subR->_bf = subRL->_bf = 0;
			}
			else
				assert(false);
		}

检查AVL树是否正常

	bool IsBalance()
		{
			return _IsBalance(_root);
		}

		bool _IsBalance(Node* root)
		{
			if (root == nullptr)
				return true;

			int LeftHeight = _Height(root->_left);
			int RightHeight = _Height(root->_right);
			if (root->_bf != RightHeight - LeftHeight)
			{
				cout << root->_kv._first <<"现在是平衡因子是:" << root->_bf << endl;
				cout << root->_kv._first <<"平衡因子应该是:" << RightHeight - LeftHeight << endl;
			}
			return abs(LeftHeight - RightHeight) < 2;
		}

		int _Height(Node* root)
		{
			if (root == nullptr)
				return 0;
			
			int leftHeight = _Height(root->_left);
			int rightHeight = _Height(root->_right);
			return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
		}

查找值

直接查找即可

		//查找
		bool Find(const K& k)
		{
			if (_root == nullptr)
				return false;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_kv.first > k)
					cur = cur->_left;
				else if (cur->_kv.first < k)
					cur = cur->_right;
				else
					return true;
			}
			return false;
		}

全部代码：


template<class K, class V>
	struct AVLNode
	{
		AVLNode<K, V>* _left;
		AVLNode<K, V>* _right;
		AVLNode<K, V>* _parent;
		int _bf; //平衡因子，记录高度差
		pair<K, V> _kv; //存储的一对数据
		//构造函数
		AVLNode(const pair<K, V>& kv)
			:_left(nullptr)
			, _right(nullptr)
			, _parent(nullptr)
			, _bf(0) //新增节点肯定是叶子节点，所以高度默认0
			, _kv(kv) {}
	};



	template <class K, class V>
	class AVLTree
	{
		typedef AVLNode<K, V> Node;
	public:
		AVLTree() :_root(nullptr){}

		bool insert(const pair<K,V>& kv)
		{
			//如果是第一次插入
			if (_root == nullptr)
			{
				_root = new Node(kv);
				return true;
			}
			Node* cur = _root; //新增节点的插入位置
			Node* parent = nullptr; //插入位置的父亲节点
			while (cur)
			{
				parent = cur;
				if (cur->_kv.first > kv.first)//新插节点的值比当前节点小，往左子树找
					cur = cur->_left;
				else if (cur->_kv.first < kv.first)
					cur = cur->_right;
				else
					return false; //不允许插入重复值的节点
			}
			cur = new Node(kv); //创建新节点
			cur->_parent = parent; //连接父亲
			if (cur->_kv.first > parent->_kv.first)
				parent->_right = cur;
			else
				parent->_left = cur;

			//节点插入成功，控制平衡因子,父亲为空，则说明调整到根节点了
			while (parent)
			{
				if (cur == parent->_right) //插入节点在父亲节点的右边
					parent->_bf++; //在右边++，在左边--
				else
					parent->_bf--;

				if (parent->_bf == 0)
				{
					//平衡因子为0，说明这棵树之前的平衡因子是-1或者1，也就是说插入新节点后变平衡了
					break;
				}
				else if (parent->_bf == 1 || parent->_bf == -1)
				{
					//父亲的平衡因子是1或者-1，说明插入之前是0，也就是说插入之前是平衡的
					//插入之后高度发生了变化，所以需要继续往上更新平衡因子
					cur = parent;
					parent = parent->_parent;
				}
				else if (parent->_bf == 2 || parent->_bf == -2)
				{
					//平衡因子为2或者-2，说明这颗树或者子树不平衡了，那么调整这颗树
					if (parent->_bf == 2 && cur->_bf == 1)//右边一边高
						RotateL(parent);
					else if (parent->_bf == -2 && cur->_bf == -1)//左边一边高
						RotateR(parent);
					else if (parent->_bf == -2 && cur->_bf == 1)
						RotateLR(parent);
					else if (parent->_bf == 2 && cur->_bf == -1)
						RotateRL (parent);

						break;
				}
				else
					assert(false);
			}
		}
		// 左单旋
		void RotateL(Node* parent)
		{
			Node* grandparent = parent->_parent;
			Node* subR = parent->_right;
			Node* subRL = subR->_left;
			//父亲连接subRL
			parent->_right = subRL;
			if (subRL)
				subRL->_parent = parent;

			//subR的左边连接parent
			subR->_left = parent;
			parent->_parent = subR;
			//grandparent连接subR
			if (grandparent == nullptr)
			{
				//grandparent为空，说明parent一开始是根节点
				_root = subR;
				subR->_parent = nullptr;
			}
			else
			{
				//如果parent一开是grandparent的左子树，则grandparent的左子树连接subR
				if (parent == grandparent->_left)
					grandparent->_left = subR;
				else
					grandparent->_right = subR;
				subR->_parent = grandparent;
			}
			//更新平衡因子
			parent->_bf = subR->_bf = 0;
		}

		//右单旋
		void RotateR(Node* parent)
		{
			Node* subL = parent->_left;
			Node* subLR = subL->_right;
			Node* grandpraent = parent->_parent;
			parent->_left = subLR;
			if (subLR)
				subLR->_parent = parent;

			subL->_right = parent;
			parent->_parent = subL;
			if (grandpraent == nullptr)
			{
				_root = subL;
				subL->_parent = nullptr;
			}
			else
			{
				if (grandpraent->_left == parent)
					grandpraent->_left = subL;
				else
					grandpraent->_right = subL;
				subL->_parent = grandpraent;
			}
			subL->_bf = parent->_bf = 0;
		}
		//左右双旋
		void RotateLR(Node* parent)
		{
			Node* subL = parent->_left;
			Node* subLR = subL->_right;
			int lrbf = subLR->_bf;

			//先左旋subL
			RotateL(subL);
			//右旋parent
			RotateR(parent);
			//保存LR的平衡因子
			if (lrbf == 0)
			{
				parent->_bf = subL->_bf = subLR->_bf = 0;
			}
			else if (lrbf == -1)
			{
				subL->_bf = subLR->_bf = 0;
				parent->_bf = 1;
			}
			else if (lrbf == 1)
			{
				subL->_bf = -1;
				subLR->_bf = parent->_bf = 0;
			}
			else
				assert(false);
		}
		//右左双旋
		void RotateRL(Node* parent)
		{
			Node* subR = parent->_right;
			Node* subRL = subR->_left;
			int rlbf = subRL->_bf;
			RotateR(subR);
			RotateL(parent);
			if (rlbf == 0)
			{
				subR->_bf = subRL->_bf = parent->_bf = 0;
			}
			else if (rlbf == -1)
			{
				subRL->_bf = parent->_bf = 0;
				subR->_bf = 1;
			}
			else if (rlbf == 1)
			{
				parent->_bf = -1;
				subR->_bf = subRL->_bf = 0;
			}
			else
				assert(false);
		}

		//查找
		bool Find(const K& k)
		{
			if (_root == nullptr)
				return false;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_kv.first > k)
					cur = cur->_left;
				else if (cur->_kv.first < k)
					cur = cur->_right;
				else
					return true;
			}
			return false;
		}

		bool IsBalance()
		{
			return _IsBalance(_root);
		}

		bool _IsBalance(Node* root)
		{
			if (root == nullptr)
				return true;

			int LeftHeight = _Height(root->_left);
			int RightHeight = _Height(root->_right);
			if (root->_bf != RightHeight - LeftHeight)
			{
				cout << root->_kv.first << "现在是平衡因子是:" << root->_bf << endl;
				cout << root->_kv.first << "平衡因子应该是:" << RightHeight - LeftHeight << endl;
			}
			return abs(LeftHeight - RightHeight) < 2;
		}

		int _Height(Node* root)
		{
			if (root == nullptr)
				return 0;

			int leftHeight = _Height(root->_left);
			int rightHeight = _Height(root->_right);
			return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
		}

	private:
		Node* _root;//AVL树的根
	};

总结🥳：

💦💦关于AVL的删除，以后有机会会为大家更新。如果有写的不好或者有错误的地方，欢迎大家指出。后序会持续为大家更新红黑树，C/C++，数据结构以及linux操作系统相关的知识，如果不嫌弃可以点个收藏加关注。谢谢大佬们了！

🔥🔥你们的支持是我最大的动力，希望在往后的日子里，我们大家一起进步！！！🔥🔥

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/175366.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

[Python从零到壹] 六十三.图像识别及经典案例篇之图像漫水填充分割应用

[Python从零到壹] 六十三.图像识别及经典案例篇之图像漫水填充分割应用

祝大家新年快乐&#xff0c;阖家幸福&#xff0c;健康快乐&#xff01; 欢迎大家来到“Python从零到壹”&#xff0c;在这里我将分享约200篇Python系列文章&#xff0c;带大家一起去学习和玩耍&#xff0c;看看Python这个有趣的世界。所有文章都将结合案例、代码和作者的经验讲…
阅读更多...
创建者模式-原型模式

创建者模式-原型模式

1.概述 用一个已经创建的实例作为原型&#xff0c;通过复制该原型对象来创建一个和原型对象相同的新对象 2.结构 原型模式包含如下角色&#xff1a; 抽象原型类&#xff1a;规定了具体原型对象必须实现的的 clone() 方法。具体原型类&#xff1a;实现抽象原型类的 clone() …
阅读更多...
Spring AOP与Spring 事务

Spring AOP与Spring 事务

一、AOP讲解 创建普通对象UserService Component public class UserService{Autowiredprivate OrderService orderService;public void test(){System.out.println(orderService);}}创建代理对象UserServiceProxy&#xff0c;对test&#xff08;&#xff09;方法进行切面编程…
阅读更多...
SSM项目 - 博客系统

SSM项目 - 博客系统

1.SSM 版本的博客系统相较于 Servlet 版本的升级1. 框架升级 : SSM (SpringBoot Spring MVC MyBatis) MySQL Redis jQuery.2. 密码升级: 明文存储/md5存储 -> 加盐处理.3. 用户登录状态持久化升级: session 持久化到内存 - > session 持久化到 Redis. (后期有空实现…
阅读更多...
cmake 03 一个可用的 cmake 工程应当是什么样的

cmake 03 一个可用的 cmake 工程应当是什么样的

cmake 学习笔记 代码地址: https://gitcode.net/u014254963/cmake-study/-/tree/master/hello_cmake_project https://gitcode.net/u014254963/cmake-study/-/tree/master/hello_cmake_project_vs 本文目标 多目录构建引用自己写的动态库关于单元测试的一些实践使用 python 脚…
阅读更多...
Pandas-DataFrame基础知识点总结

Pandas-DataFrame基础知识点总结

1、DataFrame的创建 DataFrame是一种表格型数据结构&#xff0c;它含有一组有序的列&#xff0c;每列可以是不同的值。DataFrame既有行索引&#xff0c;也有列索引&#xff0c;它可以看作是由Series组成的字典&#xff0c;不过这些Series公用一个索引。 DataFrame的创建有多种…
阅读更多...
JavaEE-多线程初阶4

JavaEE-多线程初阶4

✏️作者&#xff1a;银河罐头 &#x1f4cb;系列专栏&#xff1a;JavaEE &#x1f332;“种一棵树最好的时间是十年前&#xff0c;其次是现在” 目录多线程案例阻塞队列阻塞队列是什么生产者消费者模型标准库中的阻塞队列阻塞队列实现定时器定时器是什么标准库中的定时器实现定…
阅读更多...
(第107篇)C规范编辑笔记(十三)

(第107篇)C规范编辑笔记(十三)

往期文章&#xff1a; C规范编辑笔记(一) C规范编辑笔记(二) C规范编辑笔记(三) C规范编辑笔记(四) C规范编辑笔记(五) C规范编辑笔记(六) C规范编辑笔记(七) C规范编辑笔记(八) C规范编辑笔记(九) C规则编辑笔记(十) C规范编辑笔记(十一) C规范编辑笔记(十二) 正文&#xff…
阅读更多...
行人属性识别研究综述（二）

行人属性识别研究综述（二）

文章目录6 PAR&#xff08;行人属性识别&#xff09;算法综述6.1全局基于图像的模型6.1.1 ACN (iccvw-2015)6.1.2 DeepSAR and DeepMAR (ACPR-2015) [6]6.1.3 MTCNN (TMM-2015) [7]6.2 基于部件的模型6.2.1 Poselets (ICCV-2011)6.2.2 rad (iccv-2013)6.2.3 PANDA (cvp -2014) …
阅读更多...
Java-IO知识详解（一）

Java-IO知识详解（一）

分类分类&#xff08;传输&#xff0c;操作&#xff09;IO理解分类 - 从传输方式上字节流字符流字节流和字符流的区别IO理解分类 - 从数据操作上文件(file)数组([])管道操作基本数据类型缓冲操作打印对象序列化反序列化转换装饰者模式分类&#xff08;传输&#xff0c;操作&…
阅读更多...
迈百瑞冲刺创业板上市：关联收入占比较高，房健民为加拿大籍

迈百瑞冲刺创业板上市：关联收入占比较高，房健民为加拿大籍

撰稿|汤汤 来源|贝多财经 近日&#xff0c;烟台迈百瑞国际生物医药股份有限公司&#xff08;下称”迈百瑞“&#xff09;在深圳证券交易所提交更新后的招股书&#xff08;申报稿&#xff09;。据贝多财经了解&#xff0c;迈百瑞于2022年9月在递交IPO申请材料&#xff0c;准备…
阅读更多...
指定不同版本的pcl

指定不同版本的pcl

18.04里面安装了两个版本的pcl&#xff0c;一个是安装ros的时候安装的pcl1.8&#xff0c;另一个是安装的源码pcl1.12版本。一直相安无事&#xff0c;今天在我编译lego-loam的时候&#xff0c;突然就冲突了。卡了我两个小时&#xff0c;到处找原因&#xff0c;网上基本上没有相似…
阅读更多...
RSD高分卫星数据处理能力提升——日正射处理数千景高分数据集

RSD高分卫星数据处理能力提升——日正射处理数千景高分数据集

李国春 通常认为&#xff0c;能够单日处理几百景高分辨率对地观测卫星数据的系统就已经是非常优秀的卫星数据处理系统了。RSD此次优化将其处理能力提升超过了一个数量级&#xff0c;达到了单日正射处理数千景高分辨率卫星数据集的水平。 不仅如此&#xff0c;RSD达到如此高的…
阅读更多...
SpringBoot+Vue项目（学生信息管理系统）搭建运行

SpringBoot+Vue项目（学生信息管理系统）搭建运行

项目地址&#xff1a;学生信息管理系统 前端部分&#xff08;Vue&#xff09; 首先以管理员身份运行终端 不然运行命令时有些会报错 1.首先下载node.js 2.打开并安装node.js 3.安装完成&#xff0c;打开控制台&#xff0c;输入node -v查看是否安装完成&#xff0c;如果显示…
阅读更多...
MongoDB学习笔记【part2】数据库、文档、集合与常用命令

MongoDB学习笔记【part2】数据库、文档、集合与常用命令

一、MongoDB 概念 Mongo 与 SQL 的术语区别如下&#xff1a; SQL术语/概念MongoDB术语/概念解释/说明databasedatabase数据库tablecollection数据表 – 集合rowdocument记录 – 文档columnfield字段 – 域indexindex索引table joins表连接&#xff0c;MongoDB不支持primary k…
阅读更多...
分享121个PHP源码，总有一款适合您

分享121个PHP源码，总有一款适合您

PHP源码 分享121个PHP源码&#xff0c;总有一款适合您 下面是文件的名字&#xff0c;我放了一些图片&#xff0c;文章里不是所有的图主要是放不下...&#xff0c; 121个PHP源码下载链接&#xff1a;https://pan.baidu.com/s/1--fhiwI0gwB1a2ouivPw7g?pwdd61x 提取码&#x…
阅读更多...
监控指标解读和JVM 分析调优

监控指标解读和JVM 分析调优

1、中间件指标  当前正在运行的线程数不能超过设定的最大值。一般情况下系统性能较好的情况下&#xff0c;线 程数最小值设置 50 和最大值设置 200 比较合适。  当前运行的 JDBC 连接数不能超过设定的最大值。一般情况下系统性能较好的情况下&#xff0c; JDBC 最小值设置 …
阅读更多...
Transformers学习笔记4

Transformers学习笔记4

Tokenizernlp任务的输入都是raw text&#xff0c;model的输入需要是inputs id&#xff0c;所以tokenzier将句子转换成inputs id&#xff0c;怎么转换呢&#xff0c;有3种方式&#xff1a;word-basedsplit the text&#xff1a;按照空格来区分按照标点来区分我们会得到一个非常大…
阅读更多...
Element-UI的dialog对话组件内的tinymce弹窗被遮挡的解决办法及其它相关注意事项

Element-UI的dialog对话组件内的tinymce弹窗被遮挡的解决办法及其它相关注意事项

问题一&#xff1a;tinymce的弹窗被遮挡 问题截图 解决办法 修改层级 注意要写在 <style></style> 中&#xff0c;我当时没注意&#xff0c;写在了 <style scoped></style> 中&#xff0c;死活没反应。 <style> /* 在el-dialog中tinymce z-ind…
阅读更多...
C进阶_指针和数组试题解析

C进阶_指针和数组试题解析

农历新年即将到来&#xff0c;我在这里给大家拜年了&#xff01;祝大家新的一年心想事成&#xff0c;皆得所愿。新的一年&#xff0c;新的征程&#xff0c;愿各位继续怀揣梦想和远方&#xff0c;奔赴每一场山海。我们一起砥砺前行&#xff0c;“卯定乾坤”&#xff01; 老老少…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023