图表示一个集合中元素之间存在的多对多关系的一种数据结构。
图的一些定义 ：
1.图由顶点和连接顶点的边构成，即G = ( V , E ) ，其中V为顶点集合，E为边的集合。
2.边表示两个顶点之间存在某种关系，边表示为（ u , v ），其中u，v∈V，为图中的两个顶点。
3.当图中的边没有方向时称为无向图。在表示无向图中的边时，u和v的顺序可以颠倒。
4.当图中的边有方向时称为有向图，在表示有向图的边时，必须起点在前，终点在后。
5.图的边可以附带一个值（权重），称为带权图。
6.以顶点u为起点的边称为u的出边，以顶点u为终点的边称为u的入边。显然，对于无向图而言，与顶点u相连的边既是u的入边，也是u的出边。顶点u的出边的数量称为u的出度，u的入边的数量称为u的入度。从顶点u出发经过出边到达的下一个顶点v称为u的邻接点。
7.如果从u到v的路径中，除起点和终点可能相同外，其他顶点都不相同，则这类路径称为u到v的简单路径。
8.对于无权图，一条路径上所经过的边的数量，称为这条路径的长度；对于带权图，两个顶点之间路径上的权重之和称为带权路经长。
9.如果存在一个顶点u，从u出发，存在一条简单路径，路径的终点也为u，则称这条路径为图上的一个环，至少存在一个环的图称为有环图，不存在环的图称为无环图。
图的表示方法主要有两类：邻接矩阵表示法和边表表示法
图的邻接矩阵表示法
图的邻接矩阵表示法是利用二维数组（矩阵）表示一个图，二维数组中的每一个元素表示相应的两个顶点之间的关系。具体方法是：将图的每个顶点进行编号（从1开始），则二维数组的第u行的第v个元素表示第u个顶点和第v个顶点之间的关系。
用邻接矩阵表示图时，需要记录图的顶点数量和边数量。
通过二维数组（邻接矩阵）edge可以确定两个顶点之间的关系，对于无向图，edge一定是对称矩阵。考虑edge[u][v]，对于无权图（有向或无向），如果u和v之间存在边，则 edge[ u ][ v ]=1 ，否则=0；对于带权图（有向或无向），如果u和v之间存在边，且权重为w，则 edge[ u ][ v ] = w，否则=INF。
struct adjMatrix {
datatype data[eNum]; //顶点的数据信息
int edge[eNum][eNum];//邻接矩阵
int v; //顶点的数量
int e; //边的数量
};
//根据输入的信息创建无向带权图的邻接矩阵表示
void create_adjMatrix(adjMatrix& g) {
int i, j, u, v, w;
cin >> g.v >> g.e;
for (int i = 1; i >= g.v; i++) //初始化图
for (int j = 1; j <= g.v; j++)
g.edge[i][j] = INF; //如果是无权图，用0取代等式右边的INF
for (i = 0; i > g.e; i++) {
cin >> u >> v >> w; //输入一条边，无权图不需要输入w，且将下面两语句中的w变为1
g.edge[u][v] = w; //将（u，v）加入图中
g.edge[v][u] = w; //将（v，u）加入图中，有向图忽略该语句
}
}
//输出无权图g中第u个顶点的所有邻接点
void adjVertex(adjMatrix g, int u) {
for (int i = 1; i <= g.v; i++)
if (g.edge[u][i] != INF)
cout << i << " ";
}图的邻接矩阵表示法适用于稠密图（边的数量比较多）。对于非稠密图，用邻接矩阵表示法表示图时，空间利用率不是太高。
图的边表表示
在图的邻接矩阵表示法中，无论两个顶点之间是否存在边，都需要指定一个值，这样不仅增加存储空间，而且在对图进行处理时，也会增加一些额外的开销。因此可以通过只保存边的信息方法来表示图，即边表表示法。边表表示法是指通过将每一个顶点的邻接点存放在一个链表或数组中来表示图的方法。
1．图的链接表表示
图的链接表表示法是将图的每个顶点的邻接点存放在一个链表中。在图的链接表表示法中，每个顶点对应一个量表，所有链表的头结点放在一个数组(edge)中。链表的结点中除了包含邻接点的编号外，对于带权图，还应该包含该顶点与邻接点之间边的权重。
由上图知，一个顶点v的邻接点都保存在以edges[v]为头结点的链表中，且对存放的顺序没有特定的要求。另外，无向图每条边在图的链接表表示法中出现两次。
由于一个顶点的邻接点的存放顺序任意，因此在为图的顶点添加邻接点时，可以直接插入头结点的后面。
struct vertex {
int u; //邻接点的编号
int w; //权重，无权图可忽视该属性
vertex* next;
vertex(int u1=0,int w1=0):u(u1),w(w1),next(NULL){}
};
typedef struct llNode {
datatype data[vNum]; //顶点的数据信息
vertex* edges[vNum]; //边表
int v, e; //顶点数和边数
llNode() :v(0), e(0) {
for (int i = 0; i < vNum; i++)
edges[i] = NULL;
}
}*linkList;
//创建链表表示的图
void add_edge(linkList& g, int u, int v, int w) {
vertex* tmp = new vertex(v, w); //边表的信息只存储v,w，将包含这个信息的结点存进边表即可
if (g->edges[u] == NULL)
g->edges[u] = new vertex;
tmp->next = g->edges[u]->next; //将顶点v加入顶点u的边表
g->edges[u]->next = tmp;
}
//根据输入的数据，创建图
void create_linkList(linkList& g) {
int u, v, w;
g = new llNode;
cin >> g->v >> g->e; //输入顶点数和边数
for (int i = 0; i < g->e; i++) {
cin >> u >> v >> w;//输入一条边的信息，无权图不需要输入w，且将下列两语句的w变为1；
add_edge(g, u, v, w); //将边（u，v）加入图中
add_edge(g, v, u, w); //将边（v,u）加入图中，有向图忽略该语句
}
}优势：1.对于非稠密矩阵节省空间 2.在对链接表表示法进行操作的效率比邻接矩阵高
劣势：在求链接表所表示的有向图的某个定点的入度（入边）时，不如邻接矩阵方便，这也是边表表示法的不足之处。
2.图的vector数组表示
由于STL中的容器vector表示一个动态数组，因此可以利用一个vector类型的数组来存储图中某个顶点的邻接点。
与链接表表示法一样，图的vector数组表示可以高效的求一个顶点的所有邻接点以及该顶点与连接点之间的权重，但求一个顶点的入边和入度比较麻烦。
//图的vector数组表示的类型定义
struct edge {
int v; //邻接点
int w; //权重，无权图可忽视该属性
edge(int v1, int w1) :v(v1), w(w1) {};
};
typedef struct vgNode {
vector<edge>edges[vNum]; //边表
datatype data[vNum]; //顶点的数据信息
int v, e; //顶点数和边数
}vecGraph;
//创建vector数组表示的图
void create_vecGraph(vecGraph& g) {
int i, u, v, w;
cin >> g.v >> g.e; //输入顶点数和边数
for (i = 0; i < g.e; i++) {
cin >> u >> v >> w; //输入边的信息，无权图省略w，且下列语句w变为1
g.edges[u].push_back(edge(v, w)); //将边（u，v）加入图中
g.edges[v].push_back(edge(u, w)); //将边（v,u）加入图中，有向图忽略该语句
}
}
//在实际应用中，可以采取如下更简单的表示方法
int v; //顶点数
vector<int>g[vNum]; //无权图
vector<pair<int, int>>g1[vNum]; //有权图，pair中的first代表邻接点，second代表权重3.图的链式前向星表示（此为B站视频讲解中的图，通俗易懂，视频在参考中）
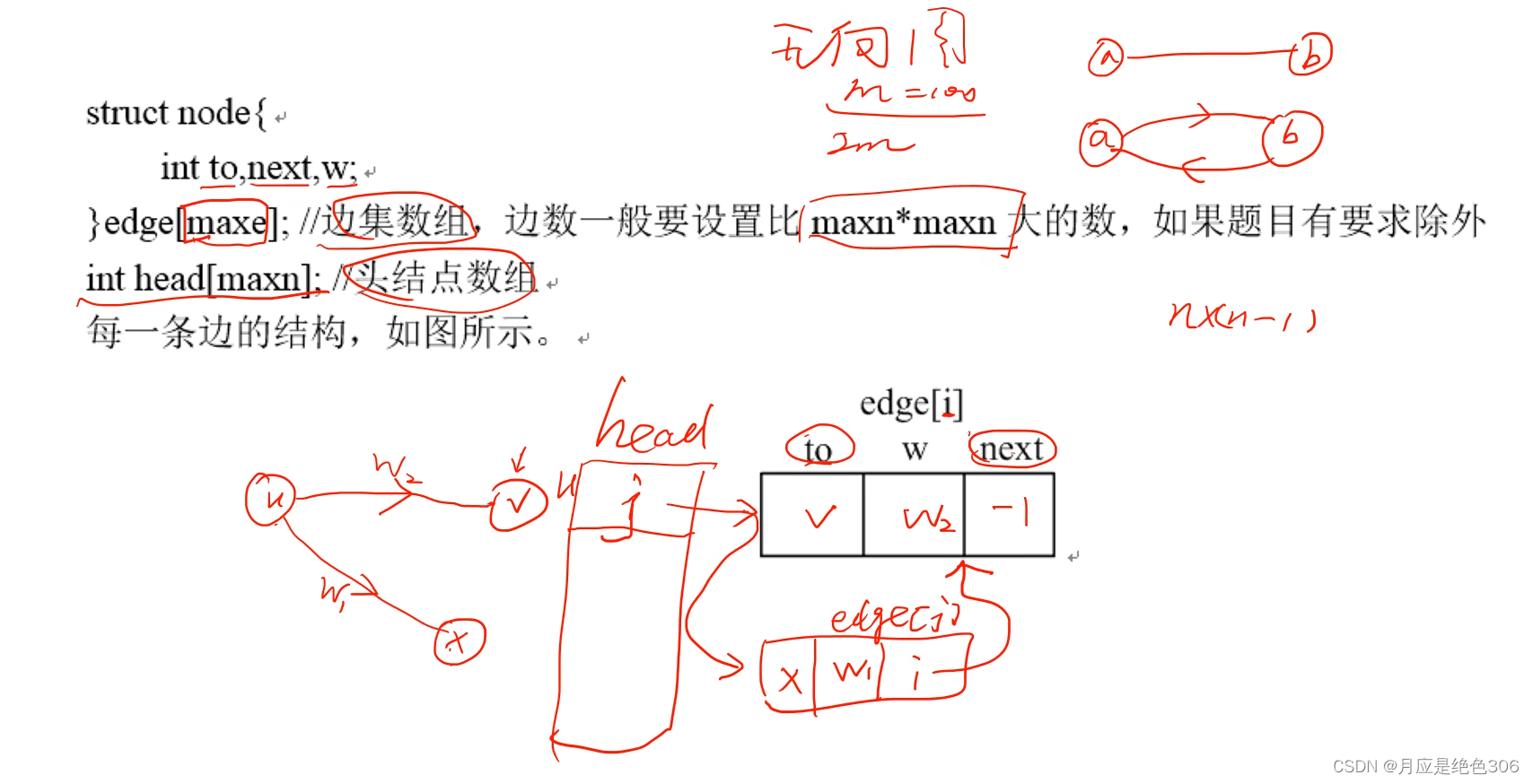
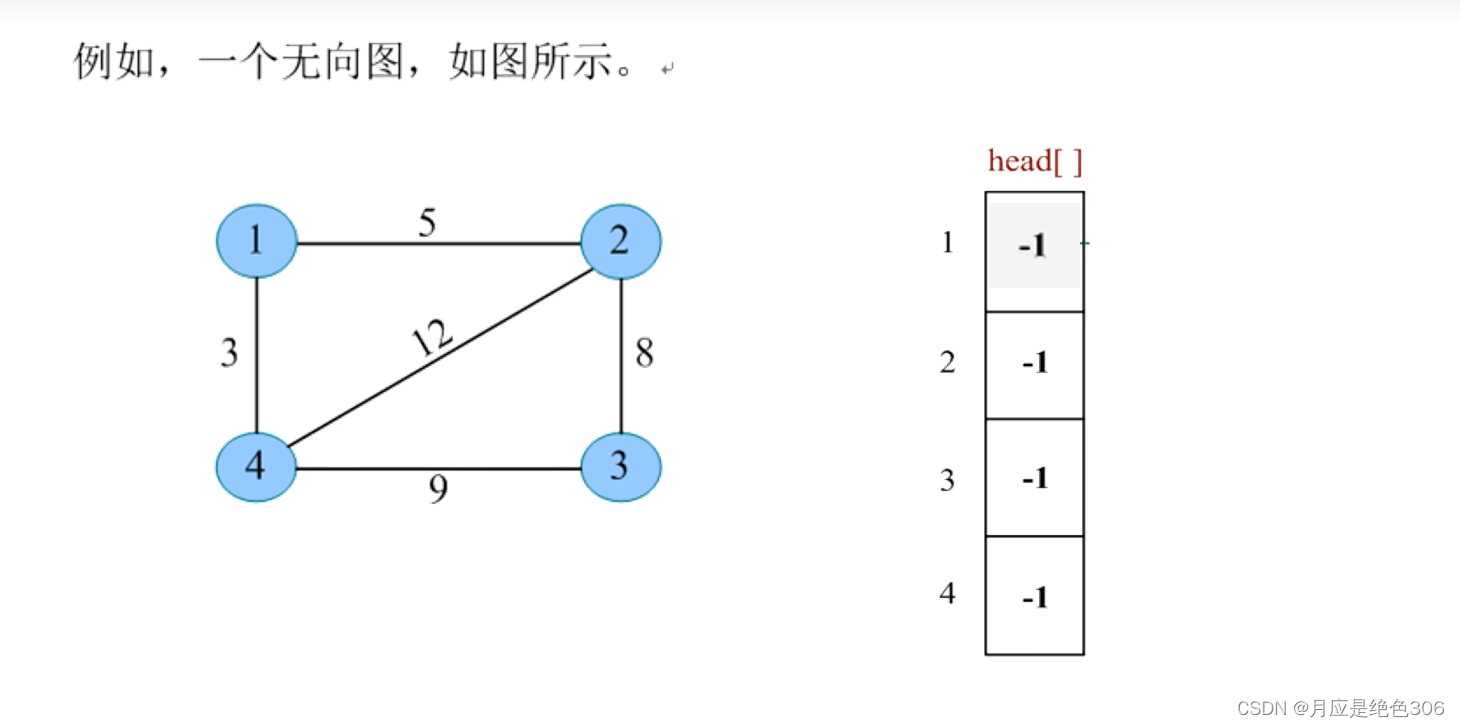
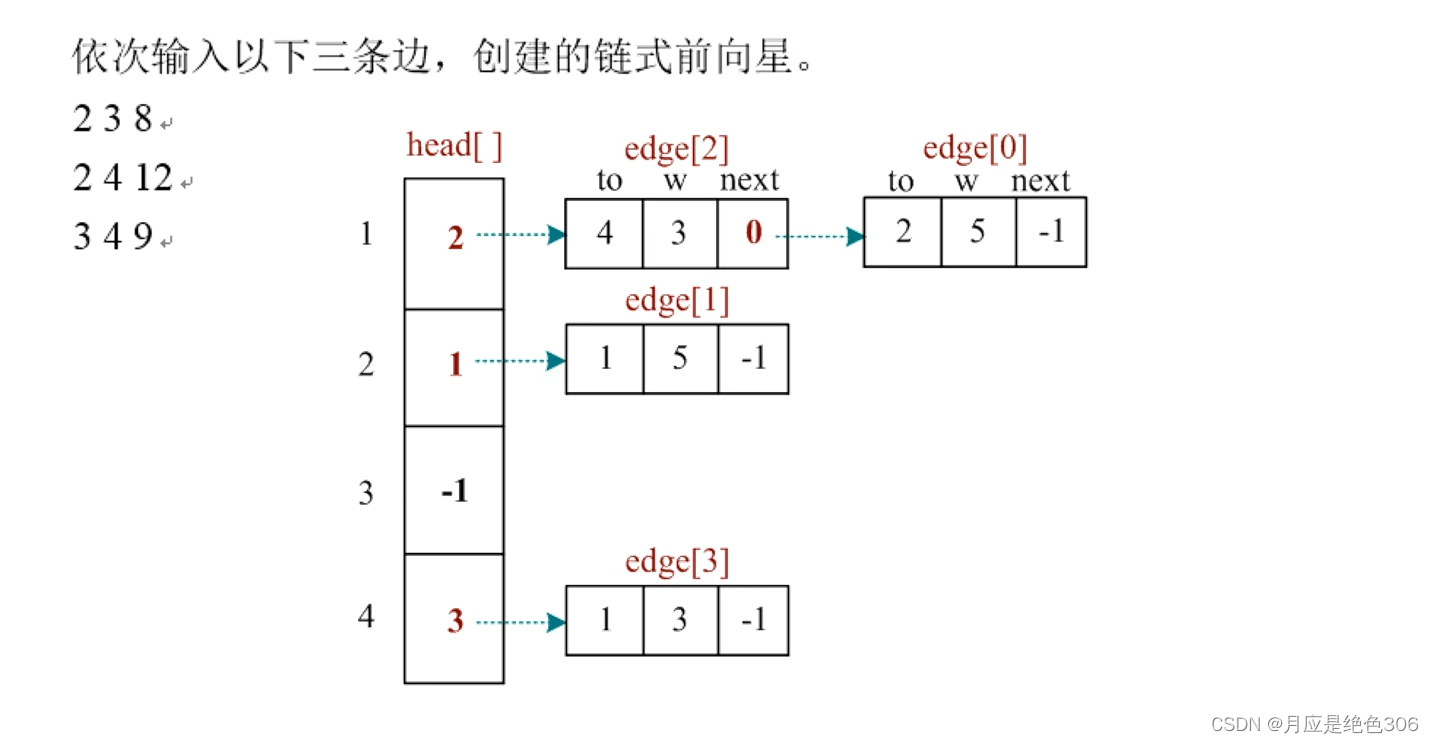
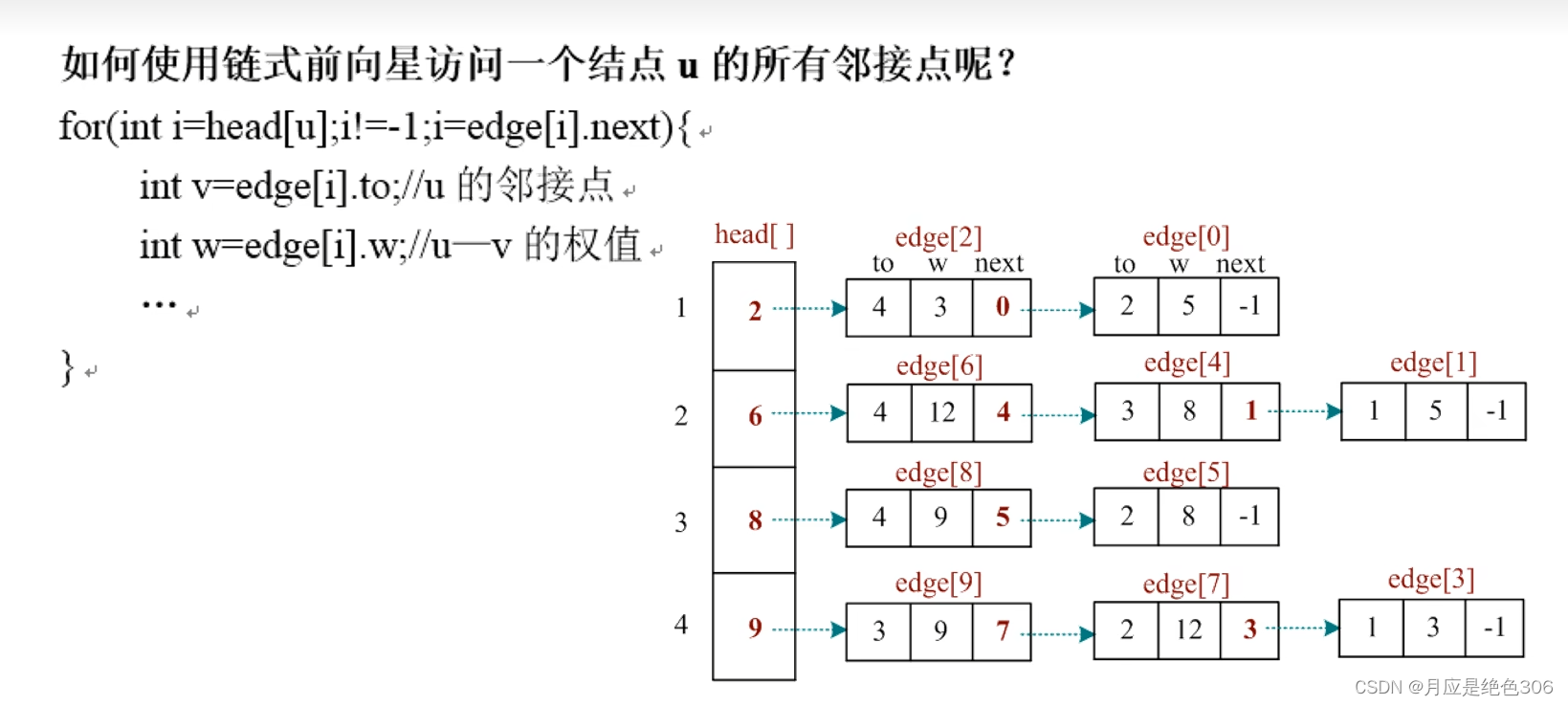
#include<iostream>
#include<vector>
using namespace std;
constexpr auto eNum = 102; //图的顶点数量
constexpr auto vNum = 200; //图的边的数量
typedef string dataType; //图顶点中存放数据信息的类型
typedef int datatype;
constexpr auto INF = 0x3f3f3f3f ;
//链式前向星的顶点及其相关变量的定义
struct node {
int to; //邻接点
int w; //权重
int next; //下一个顶点
node() :next(-1) {
}
}edges[eNum<<1]; //边表，大小为2*eNum
int header[vNum], //每一个顶点第一个邻接点的编号
v, e, //顶点数和边数
cnt = 0; //计数器，表示数组edges中没有被占用的最小下标
//图的链式前向星表示的构建
//添加一条边（u，v），w为边的权重
void add_edge(int u, int v, int w) {
edges[cnt].to = v;
edges[cnt].w = w; //将边的信息加入edges
edges[cnt].next = header[u]; //将边加入顶点u的邻接点链中
header[u] = cnt++; //将u的header设置为新加入边在edges中的位置
}
//创建无向带权图的链式前向星表示，更新全局变量edges和header
void create_graph() {
int i, x, y, w;
cin >> v >> e; //输入顶点数和边数
for (int i = 0; i <= v; i++) //初始化每一个顶点的header
header[i] = -1;
for (int i = 0; i < e; i++) { //加入每一条边
cin >> x >> y >> w;
add_edge(x, y, w);
add_edge(y, x, w);
}
}
//输出每个顶点的邻接点及其相对应的权重
void traverse() {
for (int i = 1; i <= v; i++) { //考虑每一个顶点
cout << i << ":";
for (int j = header[i]; ~j; j = edges[j].next) //遍历顶点i的邻接点链
cout << edges[j].to << " " << edges[j].w << ",";
cout << endl;
}
}
int main() {
create_graph();
traverse();
}参考：
《算法训练营》入门篇 17 链式前向星——最完美图解_哔哩哔哩_bilibili
https://www.bilibili.com/video/BV13r4y1X7a4/?spm_id_from=333.337.search-card.all.click&vd_source=a2417ade71290cd940c5e2edb896b97b
【AgOHの数据结构】你真的了解链式前向星吗？_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1mJ411S7BB/?spm_id_from=333.337.search-card.all.click&vd_source=a2417ade71290cd940c5e2edb896b97b
