给定两个数组x和hp，长度都是N。 x数组一定是有序的，x[i]表示i号怪兽在x轴上的位置 hp数组不要求有序，hp[i]表示i号怪兽的血量

news2025/11/3 18:50:18

题目描述

给定两个数组x和hp，长度都是N。
x数组一定是有序的，x[i]表示i号怪兽在x轴上的位置
hp数组不要求有序，hp[i]表示i号怪兽的血量
为了方便起见，可以认为x数组和hp数组中没有负数。
再给定一个正数range，表示如果法师释放技能的范围长度(直径！)
被打到的每只怪兽损失1点血量。
返回要把所有怪兽血量清空，至少需要释放多少次aoe技能？
三个参数：int[] x, int[] hp, int range
返回：int 次数

题目分析

贪心
我们先假设hp是紧贴在站在一起的（也就是先不看X），假设其hp如下：
在这里插入图片描述
因为最终要把所有的怪兽都杀死。

  • 我们先看第一个怪兽，其hp为5。那么不管这个怪兽是怎么死的，其一定要被AOE覆盖它5次。
    -我们每次AOE以它为起点，放五次，那么hp数组变为：
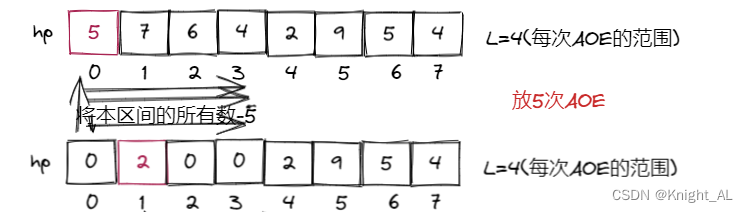
    在这里插入图片描述
  • 然后我们再找下一个大于0的怪兽，以它作为AOE的起点，以最少的次数去杀死它，得到如下：
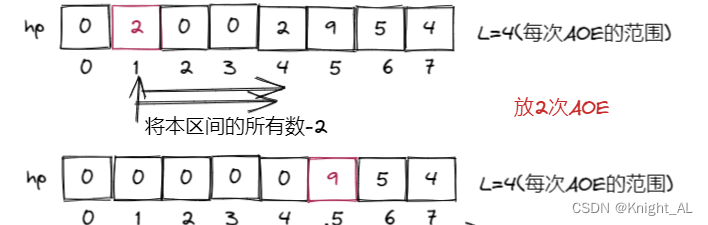
    在这里插入图片描述
  • 然后我们再找下一个大于0的怪兽，以它作为AOE的起点，以最少的次数去杀死它，得到如下：
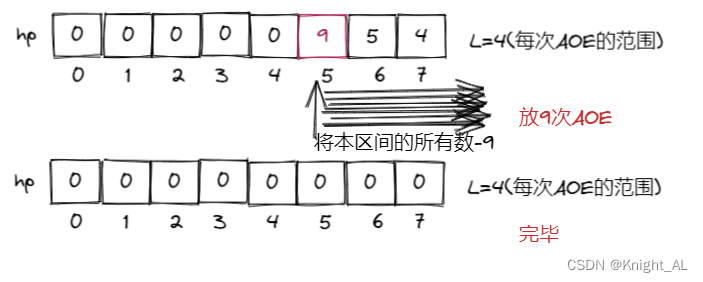    在这里插入图片描述- 下一个没有大于0的怪兽了，完毕。最终得到

贪心

举个例子：
如果怪兽情况如下，
怪兽所在，x数组  : 2 3 5 6 7 9
怪兽血量，hp数组 : 2 4 1 2 3 1
怪兽编号        : 0 1 2 3 4 5
技能直径，range = 2
int n = x.length;
int[] cover = new int[n];
首先求cover数组，
如果技能左边界就在0号怪兽，那么技能到2号怪兽就覆盖不到了
所以cover[0] = 2;
如果技能左边界就在1号怪兽，那么技能到3号怪兽就覆盖不到了
所以cover[1] = 3;
如果技能左边界就在2号怪兽，那么技能到5号怪兽就覆盖不到了
所以cover[2] = 5;
如果技能左边界就在3号怪兽，那么技能到5号怪兽就覆盖不到了
所以cover[3] = 5;
如果技能左边界就在4号怪兽，那么技能到6号怪兽（越界位置）就覆盖不到了
所以cover[4] = 6(越界位置);
如果技能左边界就在5号怪兽，那么技能到6号怪兽（越界位置）就覆盖不到了
所以cover[5] = 6(越界位置);
综上：
如果怪兽情况如下，
怪兽所在，x数组  : 2 3 5 6 7 9
怪兽血量，hp数组 : 2 4 1 2 3 1
怪兽编号        : 0 1 2 3 4 5
cover数组情况   : 2 3 5 5 6 6
技能直径，range = 2
cover[i] = j，表示如果技能左边界在i怪兽，那么技能会影响i...j-1号所有的怪兽
就是如下的for循环，在求cover数组

public static int minAoe2(int[] x, int[] hp, int range){
        int N = x.length;
        int[] cover = new int[N];
        int r = 0;
        for (int i = 0; i < N; i++) {
            while (r<N && x[r]-x[i]<=range){
                r++;
            }
            cover[i] = r;
        }
        int ans = 0;
        for (int i = 0; i < N; i++) {
            int minus = hp[i];
            if (hp[i]>0){
                for (int j = i; j < cover[i]; j++) {
                    hp[j] -= minus;
                }
                ans += minus;
            }
        }
        return ans;
    }

贪心+线段树

    // 关键点就是：
    // 1) 线段树
    // 2) 总是用技能的最左边缘刮死当前最左侧的没死的怪物
    // 3) 然后向右找下一个没死的怪物，重复步骤2)
    public static int minAoe3(int[] x, int[] hp, int range) {
        int n = x.length;
        int[] cover = new int[n];
        int r = 0;
        for (int i = 0; i < n; i++) {
            while (r<n && x[r]-x[i]<=range){
                r++;
            }
            cover[i] = r;
        }
        SegmentTree st = new SegmentTree(hp);
        st.build(1,n,1);
        int ans = 0;
        for (int i = 1; i <= n; i++) {
            int leftHP = st.query(i,i,1,n,1);
            if (leftHP>0){
                ans+=leftHP;
                st.add(i,cover[i-1],-leftHP,1,n,1);
            }
        }
        return ans;
    }

    public static class SegmentTree{
        private int MAXN;
        private int[] arr;
        private int[] sum;
        private int[] lazy;

        public SegmentTree(int[] origin){
            int MAXN = origin.length+1;
            arr = new int[MAXN];  // arr[0] 不用 从1开始使用
            for (int i = 1; i < MAXN; i++) {
                arr[i] = origin[i-1];
            }
            sum = new int[MAXN<<2];
            lazy = new int[MAXN<<2];
        }

        // 在初始化阶段，先把sum数组，填好
        // 在arr[l~r]范围上，去build，1~N，
        // rt : 这个范围在sum中的下标
        public void build(int l,int r,int rt){
            if (l==r){
                sum[rt] = arr[l];
                return;
            }
            int mid = (l+r) >> 1;
            build(l,mid,rt<<1);
            build(mid+1,r,rt<<1|1);
            pushUp(rt);
        }

        private void pushUp(int rt) {
            sum[rt] = sum[rt<<1] + sum[rt<<1 |1];
        }

        // L~R, C 任务！
        // rt，l~r
        public void add(int L,int R,int C,int l,int r,int rt){
            // 任务如果把此时的范围全包了！
            if (L<=l && r<=R){
                sum[rt] += C *(r-l+1);
                lazy[rt] += C;
                return;
            }
            int mid = (l+r)>>1;
            pushDown(rt,mid-l+1,r-mid);
            if (L <= mid){  //1-500 mid=250 但是我们要add 3-800    那么左边继续分
                add(L,R,C,l,mid,rt<<1);
            }
            if (R>mid){
                add(L,R,C,mid+1,r,rt<<1|1);
            }
            pushUp(rt);
        }

        // L~R, C 任务！
        // rt，l~r
        public int query(int L,int R,int l,int r,int rt){
            // 任务如果把此时的范围全包了！
            if (L<=l && r<=R){
                return sum[rt];
            }
            int mid = (l+r)>>1;
            pushDown(rt,mid-l+1,r-mid);
            int ans = 0;
            if (L <= mid){  //1-500 mid=250 但是我们要add 3-800    那么左边继续分
                ans += query(L,R,l,mid,rt<<1);
            }
            if (R>mid){
                ans += query(L,R,mid+1,r,rt<<1|1);
            }
            return ans;
        }

        private void pushDown(int rt, int ln, int rn) {
            if (lazy[rt] != 0){
                lazy[rt<<1] += lazy[rt];
                lazy[rt<<1|1] += lazy[rt];
                sum[rt<<1] += lazy[rt]*ln;
                sum[rt<<1|1] += lazy[rt]*rn;
                lazy[rt] = 0;
            }
        }


    }

对数器测试

package com.donglin.class01;

import java.util.Arrays;

public class AOE {

    // 纯暴力解法
    // 太容易超时
    // 只能小样本量使用
    public static int minAoe1(int[] x, int[] hp, int range) {
        boolean allClear = true;
        for (int i = 0; i < hp.length; i++) {
            if (hp[i] > 0) {
                allClear = false;
                break;
            }
        }
        if (allClear) {
            return 0;
        } else {
            int ans = Integer.MAX_VALUE;
            for (int left = 0; left < x.length; left++) {
                if (hasHp(x, hp, left, range)) {
                    minusOneHp(x, hp, left, range);
                    ans = Math.min(ans, 1 + minAoe1(x, hp, range));
                    addOneHp(x, hp, left, range);
                }
            }
            return ans;
        }
    }

    public static boolean hasHp(int[] x, int[] hp, int left, int range) {
        for (int index = left; index < x.length && x[index] - x[left] <= range; index++) {
            if (hp[index] > 0) {
                return true;
            }
        }
        return false;
    }

    public static void minusOneHp(int[] x, int[] hp, int left, int range) {
        for (int index = left; index < x.length && x[index] - x[left] <= range; index++) {
            hp[index]--;
        }
    }

    public static void addOneHp(int[] x, int[] hp, int left, int range) {
        for (int index = left; index < x.length && x[index] - x[left] <= range; index++) {
            hp[index]++;
        }
    }


    public static int minAoe2(int[] x, int[] hp, int range){
        int N = x.length;
        int[] cover = new int[N];
        int r = 0;
        for (int i = 0; i < N; i++) {
            while (r<N && x[r]-x[i]<=range){
                r++;
            }
            cover[i] = r;
        }
        int ans = 0;
        for (int i = 0; i < N; i++) {
            int minus = hp[i];
            if (hp[i]>0){
                for (int j = i; j < cover[i]; j++) {
                    hp[j] -= minus;
                }
                ans += minus;
            }
        }
        return ans;
    }


    // 正式方法
    // 关键点就是：
    // 1) 线段树
    // 2) 总是用技能的最左边缘刮死当前最左侧的没死的怪物
    // 3) 然后向右找下一个没死的怪物，重复步骤2)
    public static int minAoe3(int[] x, int[] hp, int range) {
        int n = x.length;
        int[] cover = new int[n];
        int r = 0;
        for (int i = 0; i < n; i++) {
            while (r<n && x[r]-x[i]<=range){
                r++;
            }
            cover[i] = r;
        }
        SegmentTree st = new SegmentTree(hp);
        st.build(1,n,1);
        int ans = 0;
        for (int i = 1; i <= n; i++) {
            int leftHP = st.query(i,i,1,n,1);
            if (leftHP>0){
                ans+=leftHP;
                st.add(i,cover[i-1],-leftHP,1,n,1);
            }
        }
        return ans;
    }

    public static class SegmentTree{
        private int MAXN;
        private int[] arr;
        private int[] sum;
        private int[] lazy;

        public SegmentTree(int[] origin){
            int MAXN = origin.length+1;
            arr = new int[MAXN];  // arr[0] 不用 从1开始使用
            for (int i = 1; i < MAXN; i++) {
                arr[i] = origin[i-1];
            }
            sum = new int[MAXN<<2];
            lazy = new int[MAXN<<2];
        }

        // 在初始化阶段，先把sum数组，填好
        // 在arr[l~r]范围上，去build，1~N，
        // rt : 这个范围在sum中的下标
        public void build(int l,int r,int rt){
            if (l==r){
                sum[rt] = arr[l];
                return;
            }
            int mid = (l+r) >> 1;
            build(l,mid,rt<<1);
            build(mid+1,r,rt<<1|1);
            pushUp(rt);
        }

        private void pushUp(int rt) {
            sum[rt] = sum[rt<<1] + sum[rt<<1 |1];
        }

        // L~R, C 任务！
        // rt，l~r
        public void add(int L,int R,int C,int l,int r,int rt){
            // 任务如果把此时的范围全包了！
            if (L<=l && r<=R){
                sum[rt] += C *(r-l+1);
                lazy[rt] += C;
                return;
            }
            int mid = (l+r)>>1;
            pushDown(rt,mid-l+1,r-mid);
            if (L <= mid){  //1-500 mid=250 但是我们要add 3-800    那么左边继续分
                add(L,R,C,l,mid,rt<<1);
            }
            if (R>mid){
                add(L,R,C,mid+1,r,rt<<1|1);
            }
            pushUp(rt);
        }

        // L~R, C 任务！
        // rt，l~r
        public int query(int L,int R,int l,int r,int rt){
            // 任务如果把此时的范围全包了！
            if (L<=l && r<=R){
                return sum[rt];
            }
            int mid = (l+r)>>1;
            pushDown(rt,mid-l+1,r-mid);
            int ans = 0;
            if (L <= mid){  //1-500 mid=250 但是我们要add 3-800    那么左边继续分
                ans += query(L,R,l,mid,rt<<1);
            }
            if (R>mid){
                ans += query(L,R,mid+1,r,rt<<1|1);
            }
            return ans;
        }

        private void pushDown(int rt, int ln, int rn) {
            if (lazy[rt] != 0){
                lazy[rt<<1] += lazy[rt];
                lazy[rt<<1|1] += lazy[rt];
                sum[rt<<1] += lazy[rt]*ln;
                sum[rt<<1|1] += lazy[rt]*rn;
                lazy[rt] = 0;
            }
        }


    }


    // 为了测试
    public static int[] randomArray(int n, int valueMax) {
        int[] ans = new int[n];
        for (int i = 0; i < n; i++) {
            ans[i] = (int) (Math.random() * valueMax) + 1;
        }
        return ans;
    }

    // 为了测试
    public static int[] copyArray(int[] arr) {
        int N = arr.length;
        int[] ans = new int[N];
        for (int i = 0; i < N; i++) {
            ans[i] = arr[i];
        }
        return ans;
    }

    // 为了测试
    public static void main(String[] args) {
        int N = 50;
        int X = 500;
        int H = 60;
        int R = 10;
        int testTime = 50000;
        System.out.println("测试开始");
        for (int i = 0; i < testTime; i++) {
            int len = (int) (Math.random() * N) + 1;
            int[] x2 = randomArray(len, X);
            Arrays.sort(x2);
            int[] hp2 = randomArray(len, H);
            int[] x3 = copyArray(x2);
            int[] hp3 = copyArray(hp2);
            int range = (int) (Math.random() * R) + 1;
            int ans2 = minAoe2(x2, hp2, range);
            int ans3 = minAoe3(x3, hp3, range);
            if (ans2 != ans3) {
                System.out.println("出错了！");
            }
        }
        System.out.println("测试结束");

        N = 500000;
        long start;
        long end;
        int[] x2 = randomArray(N, N);
        Arrays.sort(x2);
        int[] hp2 = new int[N];
        for (int i = 0; i < N; i++) {
            hp2[i] = i * 5 + 10;
        }
        int[] x3 = copyArray(x2);
        int[] hp3 = copyArray(hp2);
        int range = 10000;

        start = System.currentTimeMillis();
        System.out.println(minAoe2(x2, hp2, range));
        end = System.currentTimeMillis();
        System.out.println("运行时间 : " + (end - start) + " 毫秒");

        start = System.currentTimeMillis();
        System.out.println(minAoe3(x3, hp3, range));
        end = System.currentTimeMillis();
        System.out.println("运行时间 : " + (end - start) + " 毫秒");
    }

}

效率对比

下面是使用了线段树，时间复杂度O(NlogN)
在这里插入图片描述

避坑问题

树的跟节点root，那么右孩子为2*root+1
当你想要使用<<的时候注意了，root<<1 | 1或者(root<<1)+1 ,不要写成root<<1 + 1

| 是位运算符
||是逻辑运算符
+的优先级大于<<

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/174768.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Vue 快速入门(二)

Vue 快速入门(二)

1、Vue浏览器插件安装 安装地址 https://devtools.vuejs.org/guide/installation.html下载完后&#xff0c;直接将vuejs-devtools.crx文件拖到Chrome浏览器扩展程序中去即可。如图&#xff1a; 2.安装完成后&#xff0c;试试效果&#xff0c;我们打开之前写的hello.html页面看…
阅读更多...
32.Isaac教程--操纵运动规划

32.Isaac教程--操纵运动规划

操纵运动规划 ISAAC教程合集地址: https://blog.csdn.net/kunhe0512/category_12163211.html Isaac SDK 为机械臂的运动规划提供了以下组件&#xff1a; EndEffectorGlobalPlanner&#xff1a;使用逆运动学将末端执行器的笛卡尔目标转换为关节角度目标。 此小码可以接收笛卡尔…
阅读更多...
云原生技能树-容器镜像制作、发布、拉取和运行

云原生技能树-容器镜像制作、发布、拉取和运行

创建仓库 请在你自己的 gitcode.net 上创建一个仓库&#xff0c;命名为cloud_native_hello_py&#xff0c;目录结构如下&#xff1a; . ├── .dockerignore ├── .gitignore ├── Dockerfile ├── README.md └── src├── main.py└── requirements.txt其中 ma…
阅读更多...
avb校验相关与块校验原理

avb校验相关与块校验原理

一、启动校验流程 edk2/QcomModulePkg/Library/avb/VerifiedBoot.c DEBUG ((EFI_D_ERROR, "LoadImageAndAuth failed %r\n", Status)); in LoadImageAndAuth()edk2/QcomModulePkg/Application/LinuxLoader/LinuxLoader.c DEBUG ((EFI_D_ERROR, "LoadImageAndAu…
阅读更多...
docker部署redis后，修改配置文件的requirepass后无效

docker部署redis后，修改配置文件的requirepass后无效

解决方案 执行docker run命令时不要使用参数–requirepass docker部署redis流程&#xff08;问题复现&#xff09; 1. 启动redis容器 在服务器docker运行时&#xff0c;执行下列命令。&#xff08;会自动在远程仓库下载镜像&#xff09; redis: docker run \ --restartalw…
阅读更多...
高等数学【合集】

高等数学【合集】

文章目录极限计算求导计算极限计算 第一步:先看x→value确定类型第一步:先看x \rightarrow value确定类型第一步:先看x→value确定类型 7种未定型:∞∞,00,1∞,0∞,∞0,00,∞−∞7种未定型: \frac{\infty}{\infty},\frac{0}{0},1^{\infty},0^{\infty},\infty^0,0^0,\infty-\inf…
阅读更多...
win10开机后桌面无图标问题解决办法

win10开机后桌面无图标问题解决办法

本篇文章主要讲解win10下桌面无图标的问题解决办法。 日期&#xff1a;2023年1月21日 作者&#xff1a;任聪聪 主要原因&#xff1a; 这个问题的原因是资源管理器或者注册表中有垃圾注册数据导致&#xff0c;实际上和显卡没有任何关系&#xff0c;但有些情况是由于驱动问题导致…
阅读更多...
OSPF 特殊区域介绍、Stub、Totally Stub、NSSA、Totally NSSA

OSPF 特殊区域介绍、Stub、Totally Stub、NSSA、Totally NSSA

1.1.0 路由 OSPF 特殊区域介绍、Stub、Totally Stub、NSSA、Totally NSSA 特殊区域的产生和注意事项 产生&#xff1a;OSPF通过划分区域减小网络内路由器的LSDB的规模。对于那些位于AS边界的非骨干区域如果该设备是较为低端的路由器&#xff0c;则无法承受过多的路由条目。为此…
阅读更多...
前端学习第一阶段：1-4章

前端学习第一阶段：1-4章

学习总结&#xff1a;前四章学习总体来说不太难理解&#xff0c;如果时间宽裕&#xff0c;一天之内可以学完。 第一章 前端就业班课程导学 第二章 HTML5 CSS3课前导学 第三章 VSCode编辑器的使用 第四章 HTML 4-1 HTML初识 List item 01-基础班学习路线 List item 02-HTML简…
阅读更多...
【Linux_】环境变量

【Linux_】环境变量

【Linux_】环境变量 心有所向&#xff0c;日复一日&#xff0c;必有精进专栏&#xff1a;《Linux_》作者&#xff1a;沂沐沐目录 【Linux_】环境变量 什么是环境变量 常见变量 查看环境变量方法 环境变量相关的命令 通过系统调用获取或设置环境变量 环境变量通常是具有全…
阅读更多...
代码随想录算法训练营第22天 二叉树 java :235. 二叉树的最近公共祖先 701.二叉搜索树中的插入操作 450.删除二叉搜索树中的节点

代码随想录算法训练营第22天 二叉树 java :235. 二叉树的最近公共祖先 701.二叉搜索树中的插入操作 450.删除二叉搜索树中的节点

文章目录LeetCode 236. 二叉树的最近公共祖先题目讲解思路LeetCode 701.二叉搜索树中的插入操作题目讲解思路LeetCode 450.删除二叉搜索树中的节点题目讲解思路示图总结既然还是要生活&#xff0c;那么就学会主宰生活LeetCode 236. 二叉树的最近公共祖先 题目讲解 思路 求最小…
阅读更多...
【数据结构与算法】详解二叉树以及模拟实现二叉树

【数据结构与算法】详解二叉树以及模拟实现二叉树

文章目录前言:1.二叉树的定义2.二叉树的相关术语3.二叉树的性质4.特殊的二叉树5.二叉树的遍历前序遍历中序遍历后序遍历层序遍历6.获取树中节点的个数方法1:遍历思想方法2:子问题的思想7.获取叶子节点的个数方法1:遍历思想方法2:子问题的思想8.获取第K层节点的个数9.获取二叉树…
阅读更多...
链表(LinkedList)

链表(LinkedList)

链表(LinkedList) 链表是有序的列表&#xff0c;但是其在内存的存储不一定连续 由这张图我们可以看出 链表是以节点的方式来存储的&#xff0c;是链式存储 每个节点包含data域&#xff0c;next域&#xff1a;指向下一个节点 我们可以发现链表的各个节点不一定是连续存储的 …
阅读更多...
再见了HDMI Alt

再见了HDMI Alt

点击上方“LiveVideoStack”关注我们▲扫描图中二维码或点击阅读原文▲了解音视频技术大会更多信息编者按&#xff1a;其实在未能推出配套线缆和适配器的那一刻&#xff0c;HDMI Alt模式就已经没有未来了。HDMI已全面落后DisplayPort。本文来自Arstechnica。文/Scharon Hardin…
阅读更多...
【SpringCloud】Nacos的安装与启动

【SpringCloud】Nacos的安装与启动

【SpringCloud】Nacos的安装与启动 一、下载安装包 二、解压 三、端口配置 四、启动 五、访问 【SpringCloud】Nacos的安装与启动 一、下载安装包 在Nacos的GitHub页面&#xff0c;提供有下载链接&#xff0c;可以下载编译好的Nacos服务端或者源代码&#xff1a; GitHu…
阅读更多...
分享149个PHP源码，总有一款适合您

分享149个PHP源码，总有一款适合您

PHP源码 分享149个PHP源码&#xff0c;总有一款适合您 下面是文件的名字&#xff0c;我放了一些图片&#xff0c;文章里不是所有的图主要是放不下...&#xff0c; 149个PHP源码下载链接&#xff1a;https://pan.baidu.com/s/1RKnEbbhpfUndnMrxG8rSIQ?pwd0nqp 提取码&#x…
阅读更多...
LINUX学习之文本编辑器VIM/VI(八)

LINUX学习之文本编辑器VIM/VI(八)

简介 VI 是 Unix 操作系统和类 Unix 操作系统中最通用的文本编辑器 VIM 编辑器是从 VI 发展出来的一个性能更强大的文本编辑器。可以主动的以字体颜色辨别语法的正确性&#xff0c;方便程序设计 VIM 与 VI 编辑器完全兼容 模式转换 如下图所示&#xff0c;一般模式下输入i、…
阅读更多...
选出相似的文本按照相似度排序difflib.get_close_matches

选出相似的文本按照相似度排序difflib.get_close_matches

【小白从小学Python、C、Java】 【计算机等级考试500强双证书】 【Python-数据分析】 选出相似的文本 按照相似度排序 difflib.get_close_matches 选择题 对于以下python代码表述错误的是? from difflib import get_close_matches myText"python" myList[&…
阅读更多...
23种设计模式（十六）——备忘录模式【状态变化】

23种设计模式（十六）——备忘录模式【状态变化】

备忘录模式 文章目录 备忘录模式意图什么时候使用备忘录真实世界类比备忘录模式的实现备忘录模式的优缺点亦称：调解人、控制器、Intermediary、Controller、Mediator 意图 在不破坏封装的前提下，捕获一个对象的内部状态，并在该对象之外保存这个状态，这样可以在以后将这个对…
阅读更多...
穿越万年的轮回[期望dp]

穿越万年的轮回[期望dp]

首先我们设置dpi,0/1,0/1dp_{i,0/1,0/1}dpi,0/1,0/1​表示经过iii次操作之后开头为red/edrred/edrred/edr&#xff0c;结尾为red/edrred/edrred/edr的串的期望redredred字符串个数。 然后我们考虑转移&#xff1a; 首先我们要来思考一下期望的本质&#xff0c;这样一个状态&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023