LeetCode 236. 二叉树的最近公共祖先

题目讲解

思路

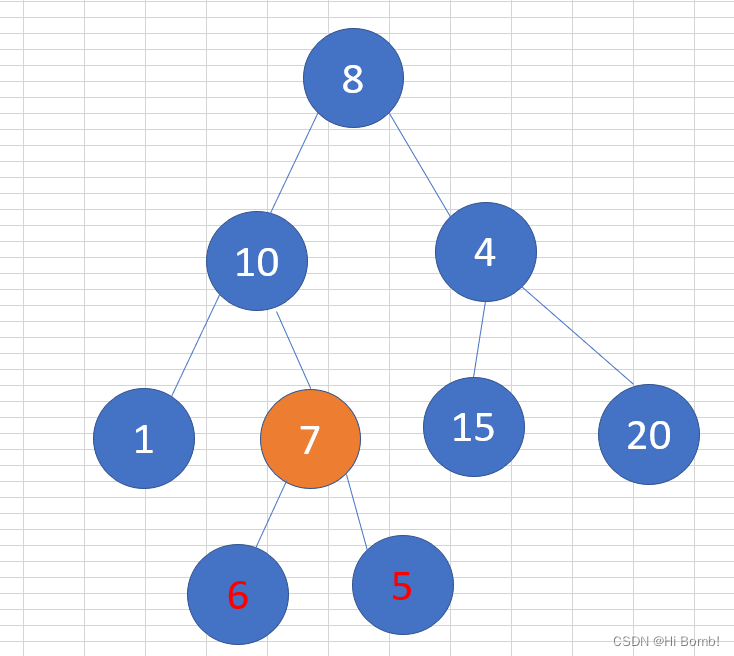
求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从底向上的遍历方式。
在回溯的过程中，必然要遍历整棵二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。
要理解如果返回值left为空，right不为空为什么要返回right，为什么可以用返回right传给上一层结果

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if( root==null || root ==p|| root== q)
        {
            return root;
        }

        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        if( right== null&& left== null)
        return null;
        else if( left ==null && right !=null)
        return right;
        else if(right ==null &&left!=null)
        return left;
        else
        return root;
    }
}

LeetCode 701.二叉搜索树中的插入操作

题目讲解

思路

只要遍历二叉搜索树，找到空节点插入元素就可以了，那么这道题其实就简单了。
在这里插入图片描述

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if( root ==null)
        {
            return new TreeNode(val);
        }
        if( val>root.val)
        root.right = insertIntoBST(root.right,val); 
        if( val<root.val)
        root.left = insertIntoBST(root.left,val);
        return root;

    }
}

LeetCode 450.删除二叉搜索树中的节点

题目讲解

思路

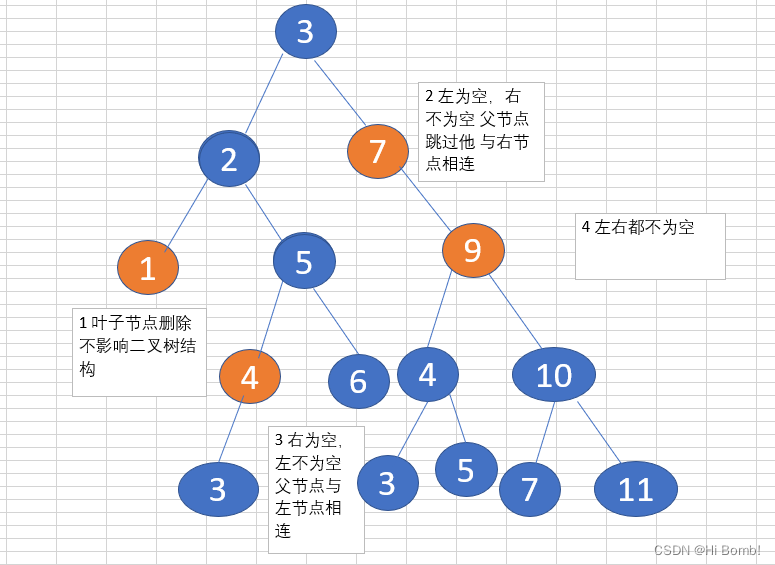
分成了五种情况进行讨论

找不到要删除的点
删除的点为叶子节点
左节点为空右节点不为空 if( root.left ==null) return root.right;
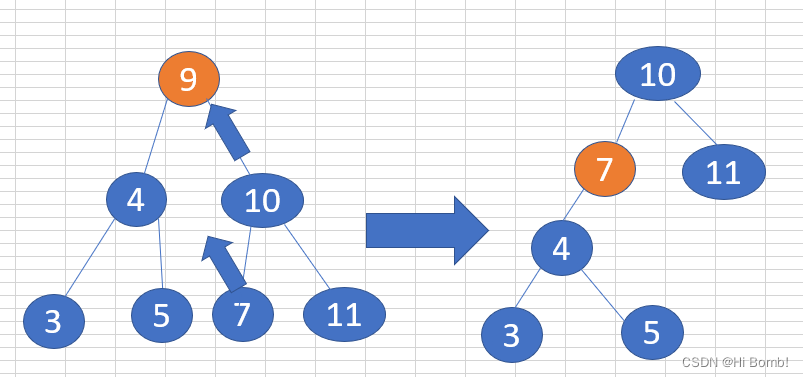
右节点为空，左节点不为空 if( root.right ==null ) return root.left;
找到要删除的点两边都是不为空
//先创建一个临时节点

TreeNode tmp = root.right
while( root.left !=null)
{
   tmp. left = root.left
   }
   root.val = tmp.val;
   root.right = delete( root.right,tmp.val);
   }
  return root;

上面是部分代码的梗概

示图

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
     
    root =delete(root,key);
    return root;
    }

    public TreeNode delete(TreeNode root, int key)
    {
        if( root ==null)
        return null;
        // 左搜索
       if( root.val> key)
         root.left = delete(root.left,key);
        //右搜索
        else if( root.val <key)
        {
            root.right = delete(root.right,key);
        }
       
        else   //平层的逻辑
        {
           if( root.left ==null) return root.right;
           if(root.right ==null ) return root.left;
            TreeNode temp = root.right;
            while(temp.left!=null)
            {
                temp=temp.left;
            }

            root.val = temp.val;
            root.right = delete(root.right,temp.val);
        }
        return root;

    }
}