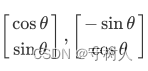投影矩阵和最小二乘法
投影矩阵
**投影矩阵P与向量b相乘将会把投影到的列空间A中。**那么现在我们来考虑两个极端的例子，这两个极端的例子将会加深我们对投影矩阵的理解。
-
如果b在矩阵A的列空间里，那么 Pb = b
-
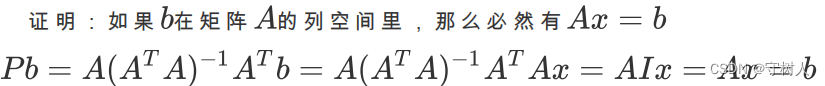
如果b垂直于矩阵A的列空间，那么Pb=0
综上所述：向量b总可以分为两个分量，一个分量在A的列空间中，另一个分量垂直于A的列空间（也即在A的左零空间中）。而上述投影矩阵的作用就是保留列空间中的分量p，去掉左零空间中的分量e。
最小二乘法
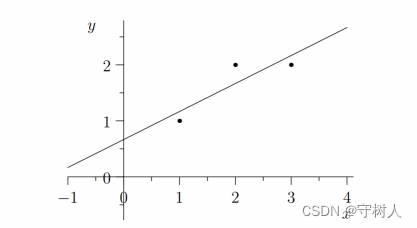
没有直线能经过图中的三个点，所以我们需要找到一条最优的直线y = C + Dx 来拟合图中的三个
点，这里的最优指的是该直线距离图中三个点(1,1),(2,2),(3,2) 的总误差最小！
根据以上条件可以得到方程组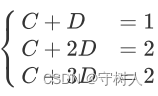
写作矩阵形式有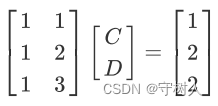
也就是我们的Ax = b，显然该方程组无解。
在寻求最优解之前，我们需要先定义总误差是什么，因为总误差能够衡量直线是否是更优的，定义了总
误差我们才能通过最小化这个量，来找到最好的C和D（也即最优的直线）。
这里，我们定义误差为
的模长的平方来作为误差，也即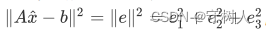
，我们要求其最小平方和（也即最小二乘）。
标准正交向量组
有一种线性无关的情况是比较特殊的：互相垂直的各列一定是线性无关的。
更特殊地，我们会要求互相垂直的单位向量（标准正交），比如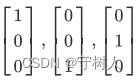 
，这些向量所组成的向量组一般被称为标准正交向量组，标准正交向量组中的向量互相垂直（正交）且为单位向量（标准）
同样的标准正交向量组还有：
