一、前言
本文主要介绍图的一些基础知识,不会太深奥,够用就行。我们以民国最出名的七角恋人物关系图为例进行讲解。
二、图的概念
图(Graph)可以用来描述实体之间的关系。
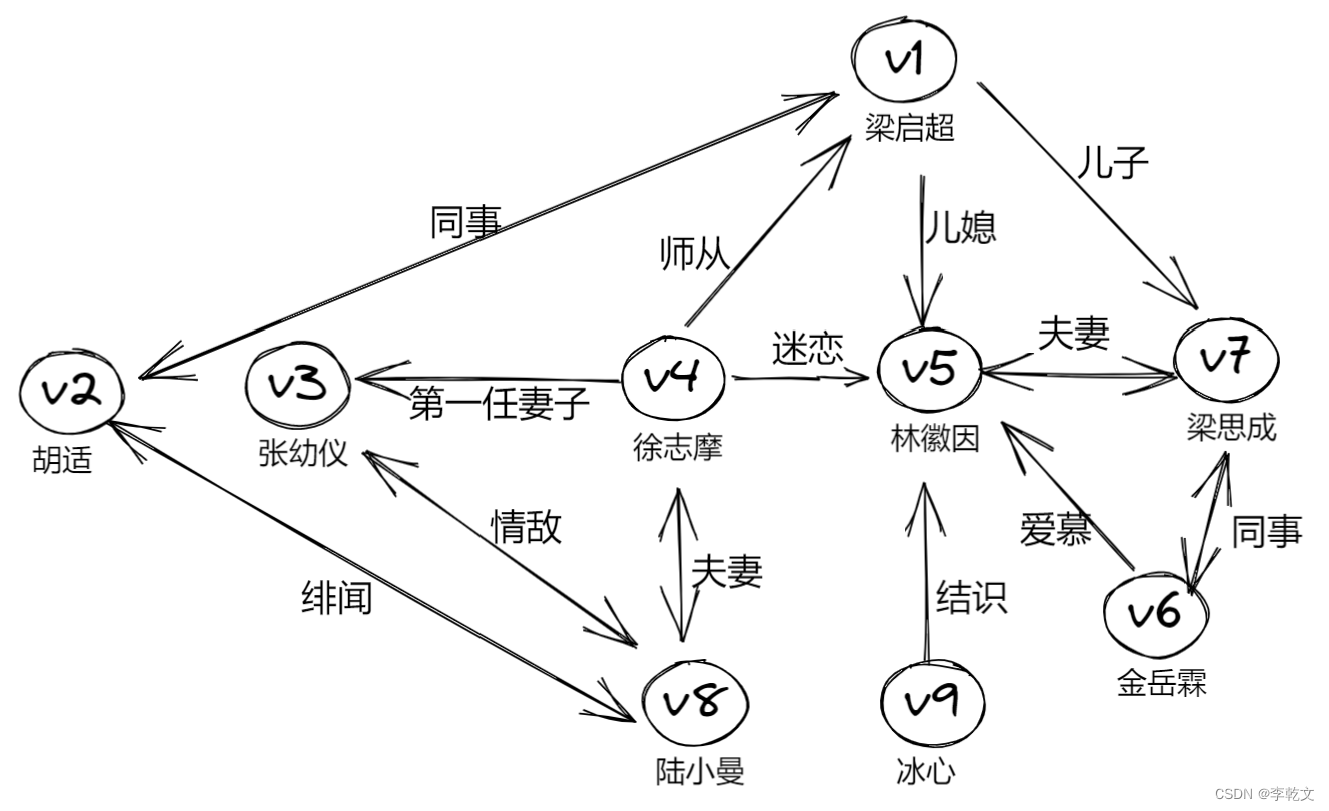
如下图所示,一张图捋清民国最出名的七角恋(摘自全历史):
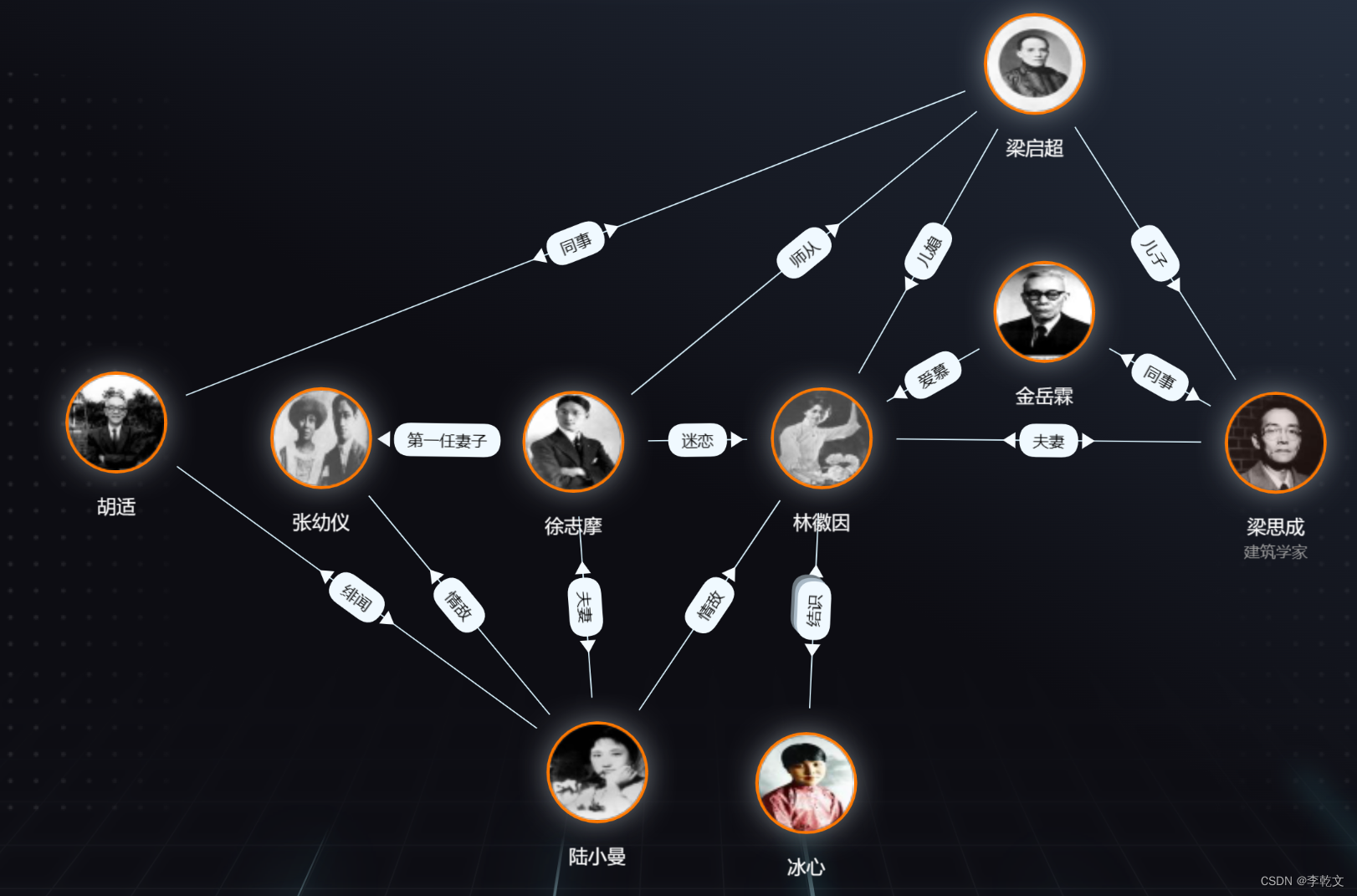
这是一张图,包括人物实体以及人物关系。我们抽象成下面的形式,人物是图的顶点(Vertex)、人物关系是图的边(Edge)。顶点(节点)和边都可以附带各自的属性(如:姓名、关系类型等)。
二、图的表示
上面的带箭头符号的边是有方向的,是有向图。我们进一步抽象,把属性和边方向去掉,变成一张简单的无向图:

如上图所示,图
G
\mathcal{G}
G包含9个顶点、13条边。我们可以表示为:
G
=
{
V
,
E
}
\mathcal{G=\{V,E\}}
G={V,E},其中:
V
=
{
v
1
,
v
2
,
…
,
v
9
}
\mathcal{V=\{v_1,v_2,\dots,v_9\}}
V={v1,v2,…,v9},
E
=
{
e
1
,
e
2
,
…
,
e
13
}
\mathcal{E=\{e_1,e_2,\dots,e_{13}\}}
E={e1,e2,…,e13}
但是,我们需要用计算机来进行图计算,那么在计算机里怎么表示一张图呢?
如下图,我们用一张二维图表表示图
G
\mathcal{G}
G,
1
1
1 表示两个顶点之间存在关系。
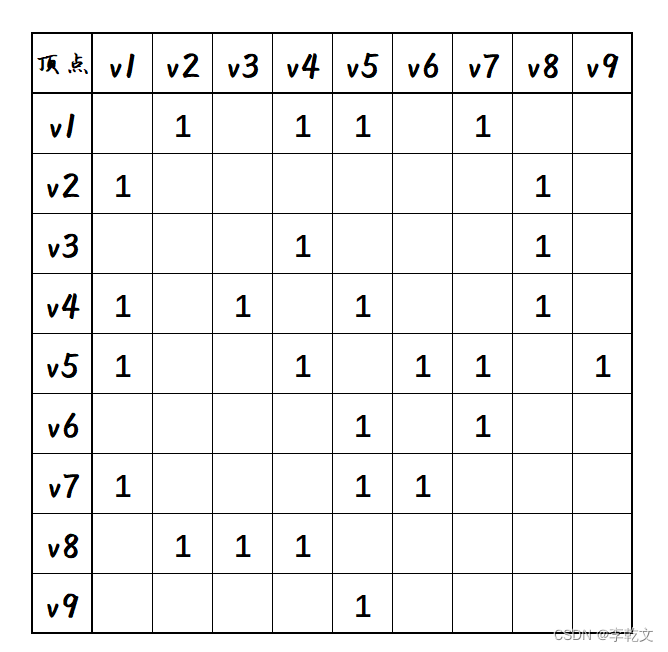
如果我们空白处用
0
0
0 填充,那么就形成了一个矩阵
A
A
A,这个矩阵叫做邻接矩阵,等价于图
G
\mathcal{G}
G,可以简单地用二维数组存储,如下:
A
=
(
0
1
0
1
1
0
1
0
0
1
0
0
0
0
0
0
1
0
0
0
0
1
0
0
0
1
0
1
0
1
0
1
0
0
1
0
1
0
0
1
0
1
1
0
1
0
0
0
0
1
0
1
0
0
1
0
0
0
1
1
0
0
0
0
1
1
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
)
A=\begin{pmatrix} 0&1&0&1&1&0&1&0&0 \\ 1&0&0&0&0&0&0&1&0 \\ 0&0&0&1&0&0&0&1&0 \\ 1&0&1&0&1&0&0&1&0 \\ 1&0&0&1&0&1&1&0&1 \\ 0&0&0&0&1&0&1&0&0 \\ 1&0&0&0&1&1&0&0&0 \\ 0&1&1&1&0&0&0&0&0 \\ 0&0&0&0&1&0&0&0&0 \\ \end{pmatrix}
A=
010110100100000010000100010101010010100101101000010100100011000011100000000010000
三、图的性质
为了方便对比参考,把上面的图贴到这里:

3.1 度
一个节点的度就是与之相连的边的条数。例如顶点
v
1
v_1
v1有
e
1
、
e
2
、
e
3
e_1、e_2、e_3
e1、e2、e3 三条边,则度为3;同理
v
2
v_2
v2的度为2、
v
3
v_3
v3的度也为2。
在有向图中,根据边的方向还分为出度和入度。
3.2 连通性
如果通过一个节点的边,可以到达图的任意节点,那么这个图是连通图,反正为非连通图。
3.3 子图
指图的一部分。
3.3 中心性
度中心性
节点
v
v
v的度中心性=
顶点
v
的度
n
−
1
\frac{顶点v的度}{n-1}
n−1顶点v的度,
n
n
n为图的节点数量。
例如
v
1
v_1
v1的度中心性为
3
9
−
1
=
0.375
\frac{3}{9-1}=0.375
9−13=0.375,
v
2
v_2
v2的度中心性为
2
9
−
1
=
0.25
\frac{2}{9-1}=0.25
9−12=0.25