文章目录
- 一、自下而上分析基本问题
- 二、算符优先分析
- 构造FIRSTVT(P)的算法
- 构造LASTVT(P)的算法
- 构造优先表的算法
- 三、LR分析法
- 1.LR(0)
- 构造LR(0)项目集规范族
- 构造识别活前缀的DFA
- 构造LR(0)分析表
- 2.SLR
- SLR解决冲突办法
- SLR(1)分析表的构造算法
- 3.LR(1)【规范LR】
- LR(1)项目集I的闭包
- 状态转换函数GO
- LR(1)项目集规范族构造
- LR(1)分析表的构造算法
- 4.LALR
- LALR分析表的构造算法
- 例题
- 结论
一、自下而上分析基本问题
归约
本章讨论的自下而上分析法是一种“移进-归约”法。
即:利用一个栈来存放符号,首先把输入符号一个一个移进栈中,当栈顶的若干字符形成某个产生式的候选式时,则把这部分替换成该产生式的左部符号。
“可归约串”的定义有多种方法:
(1) 算符优先分析法: “最左素短语”
(2) 规范归约分析法: “句柄”
自下而上的分析过程也可用一棵语法树来表示,即先建子树,随着归约的完成,连成一棵语法树。
规范归约简述

一个句型的句柄是这个句型的语法树中最左深度为2的子树的叶子从左到右排列。


在形式语言中,最右推导常称为规范推导。由规范推导所得的句型称为规范句型。
若文法是无二义的,则规范推导的逆过程,必是规范归约。
对于规范句型,句柄的后面不会出现非终结符,即只能全是终结符。(原因:对于移进-归约来说,这是由句柄的“最左”特征决定的。)
规范归约的实质:
在移进的过程中,当发现栈顶呈现句柄时,就用相应的产生式的左部符号来替换。
符号栈的使用与语法树的表示
例如5.3 写出输入串i*i+i的规范归约过程:
步骤 栈 输入串 动作
0 # i*i+i# 预备
1 #i *i+i# 进栈
2 #F *i+i# 归约
3 #T *i+i# 归约
4 #T* i+i# 进栈
5 #T*i +i# 进栈
6 #T*F +i# 归约
….
12 #E+T # 归约
13 #E # 归约
14 #E # 接受
二、算符优先分析
它是一种简单、广为使用的自下而上分析法。特别有利于表达式的分析过程。
算符优先分析法不是一种规范归约法。
算符优先分析(Operator Precedence Parsing)
定义算符之间(即终结符之间)的某种优先关系,借助这种优先关系来寻找“可归约串”和进行归约。
基本思想
算符优先分析法是一种简单、直观、广为使用的自下而上语法分析方法,它是依据算术表达式的四则运算过程而设计的一种方法,也适用于对一般的高级语言程序的分析。
算符优先分析法的基本思想是,首先确定运算符(确切地说是终结符)之间的优先关系和结合性质,然后借助这种关系,比较相邻运算符之间的优先级来确定句型的可归约串,并进行归约。
值得注意的是,算符优先分析过程虽然是自下而上归约过程,但它的可归约串未必是句柄,也就是说,算符优先分析过程不是一种规范归约。
算法优先关系有三种:
a < b a的优先性低于b
a = b a的优先性等于b
a > b a的优先性高于b
注意
a > b 并不意味着 b < a,即不满足对称性



构造FIRSTVT§的算法
有两条规则:
(1)若有产生式 P->a……或 P->Qa……
则 a∈ FIRSTVT(P)
(2) 若有产生式 P->Q……
则对任意a∈ FIRSTVT(Q),
都有a∈ FIRSTVT(P)
构造LASTVT§的算法
有两条规则:
(1)若有产生式 P->……b 或 P->……bQ
则 b∈ LASTVT(P)
(2) 若有产生式 P-> ……Q
则对任意 b∈ LASTVT(Q),
都有b∈ LASTVT(P)。
构造优先表的算法
For 每个P->x1X2 …Xn do
for i:=1 to n do begin
if Xi和Xi+1都是终结符 then Xi = Xi+1 ;
if Xi和Xi+2都是终结符,且Xi+1是非终结符,
then Xi = Xi+2 ; (i<=n-2)
if Xi是终结符,Xi+1是非终结符 then
for FirstVT(Xi+1)的每个a do Xi < a ;
if Xi是非终结符,Xi+1是终结符 then
for LastVT(Xi)的每个a do a > Xi+1 ; end.


素短语:至少含有一个终结符的短语,且除它自身外不再含有任何更小的素短语。
最左素短语:句型中最左边的素短语。
在算符优先文法中,用“最左素短语”来刻画可归约串。

算符优先分析算法
k=1;
S[k]=‘#’;
Repeat
读一个输入字符a
if S[k] ∈VT then j:=k else j:=k-1 ;
while S[j] > a do
{ 从栈中取出最左素短语->归约到某个N;
N进栈 }
if S[j] < a or S[j] = a then { a进栈 }
else error;
Until a=‘#’
算法工作完毕后,符号栈S呈现#N#
某个非终结符号N是指那样一个产生式的左部符号,此产生式的右部和S[j+1]…S[k]构成如下一 一对应关系:自左向右,终结符对终结符,非终结符对非终结符,而且对应的终结符相同。
例5.4:对 P90 文法(5.3),
(1)E->E+T|T
(2)T->T*F|F
(3)F->P↑F|P
(4)P->(E)|i
分析句子 i+i
0 # i+i# 预备
1 #i +i# 进栈 (∵ # < i )
2 #P +i# 归约 (∵ i > + )
3 #P+ i# 进栈 (∵ # < + )
4 #P+i # 进栈 (∵ + < i )
5 #P+P # 归约 (∵ i > # )
6 #E # 归约 (∵ + > # )
7 #E# 接受 (∵ # = # )
若输入串正确,则符号栈里为#S#;
比规范归约分析要快得多( 跳过所有的单非产生式所对应的归约步骤,单非产生式:右部仅含一个非终结符的产生式,例如P->Q)
可能把不是句子的输入串误认为是句子(忽略了非终结符的作用) 适用于分析各类表达式的正确性。
优先函数





优先函数:
优点: 便于作比较运算,且节约存储空间(n^2->2n);
缺点: 原来不存在优先关系的两个终结符,由于与自然数相对应,变成可比较了。注意 一个优先关系表的优先函数不是唯一的; 有的优先关系表可能不存在其对应的优先函数。
三、LR分析法
LR分析法是一种有效的自下而上的分析技术,可用于很大一类上下文无关文法(包括LL(1))的语法分析。
L:表示从左到右扫描输入串;
R:表示构造一个最右推导的逆过程。
本章讨论四种LR分析表的构造方法:
LR(0) SLR
规范LR LALR
LR分析法的优缺点
1.能识别几乎所有能用CFG描述的程序设计语言的结构;
2.目前最一般的无回溯移进规约语法分析法,可以有效的实现;
3.是LL文法类的真超集;
4.在自左向右扫描输入串时,能准确发现出错位置;
5.用手工构造分析程序时,工作量太大,主要体现在分析表的构造。
1.LR(0)
LR(0)项目:在文法的每个产生式的右部添加一个点就称为一个LR(0)项目。
例如:产生式 A->XYZ 对应四个项目:
A->. XYZ
A->X .YZ
A->XY. Z
A->XYZ.
一个项目指明了在分析过程中的某时刻,我们看到了产生式的多大部分。
注意:对于A->ε,只对应一个项目 A-> .
LR(0)文法
对文法G的拓广文法G’,若识别所有活前缀的DFA的每个状态不含有冲突,则称G是一个LR(0)文法。
即:它的LR(0) 规范族C中的每个项目集都不是冲突项目集。

构造LR(0)项目集规范族
LR(0)项目集规范族:
构成识别一个文法所有活前缀的DFA的状态(项目集)的全体,称为这个文法的LR(0)项目集规范族。
项目集I的闭包closure(I)定义和构造

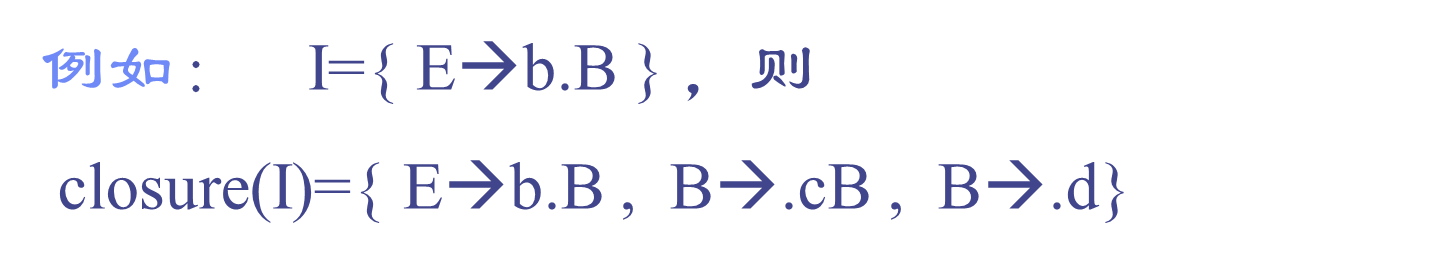
状态转换函数GO的定义

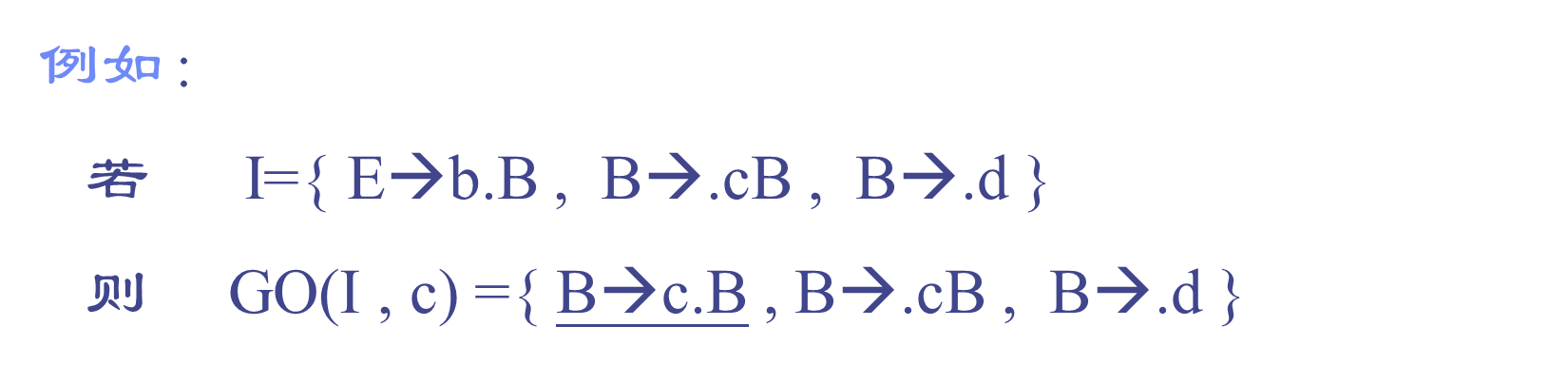
LR(0)项目集规范族 C 的构造算法
Procedure itemset(G’)
begin C:={ Closure(S’.S) };
repeat
for I ∈ C and x∈Vt∪VN do
if GO(I , x) not in C then
把 GO(I , x)加入到C
until C不再增大
End;
冲突项目集
若一个项目集里,既含有移进项目又含有归约项目,或含有多个不同的归约项目,则说该项目集含有冲突。

构造识别活前缀的DFA


构造LR(0)分析表


● LR(0)分析表:按上述算法构造的分析表,若没有多重定义入口,则称为LR(0)分析表。
● LR(0)文法:具有LR(0)分析表的文法。
● LR(0)分析器:使用LR(0)分析表的分析器。
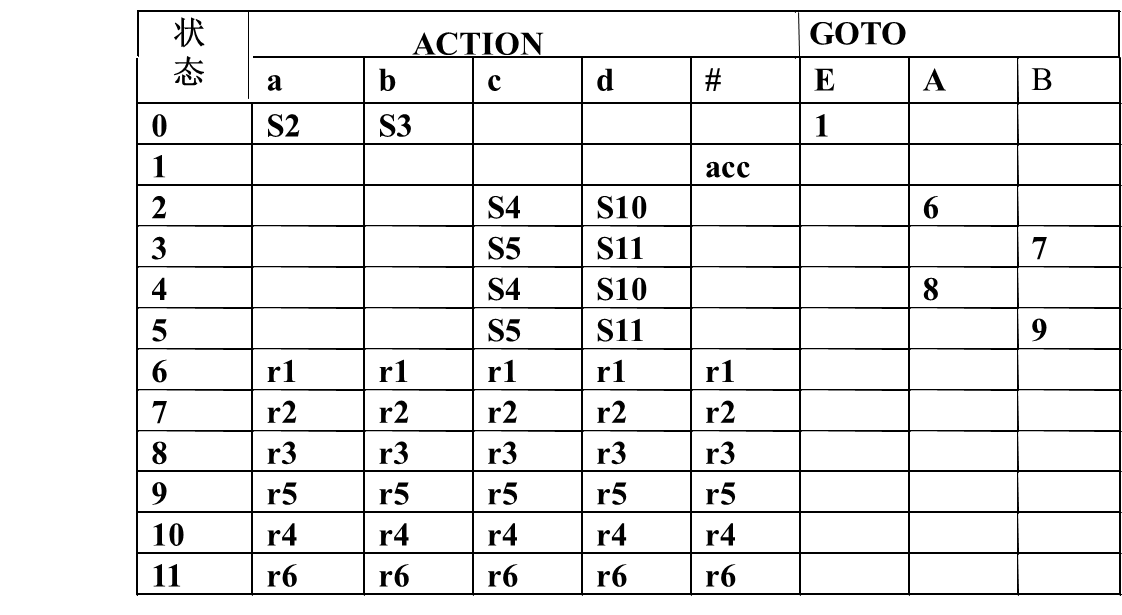
例如 对文法(5.7),
S’->.E
E->aB|bB
A->cA|d
B->cB|d
写出输入串 accd 的LR(0)分析过程。


2.SLR
SLR(1)分析表:按上述算法构造的分析表若没有多重定义入口,则称为SLR分析表。 SLR(1)文法:具有SLR分析表的文法。
SLR(1)分析器:使用SLR(1)分析表的分析器。

SLR解决冲突办法


SLR(1)分析表的构造算法


若一个文法是LR(0)的,则一定是SLR(1)的;
每个SLR(1)文法都是无二义的。
当然,无二义的文法未必是SLR(1)的。
3.LR(1)【规范LR】
在SLR方法中,可能会存在无效的归约。
解决办法:
希望每个状态含更多的“展望”信息,以便能消除动作冲突 或 排除无效归约。
必要时,将状态进行分裂,使得LR分析器的每个状态能确切指出,当一个归约项目后跟哪些终结符时,才允许归约。



LR(1)项目集I的闭包


状态转换函数GO

LR(1)项目集规范族构造
Procedure itemset(G’)
begin C:={ I0=Closure( [S’.S , #] ) };
repeat
for I∈ C and X∈Vt∪VN do
if GO(I , X) not in C then
把 GO(I , X)加入到C
until C不再增大
End;

LR(1)分析表的构造算法


规范LR分析表:按上述算法构造的分析表,若没有多重定义入口,则称为规范的LR(1)分析表。
LR(1)文法:具有规范LR(1)分析表的文法。
LR(1)分析器:使用规范LR(1)分析表的分析器。
4.LALR
LALR方法,是一种折中方法。
它的分析表比LR(1)分析表要小,能力也差一点,但它能解决一些SLR所不能对付的情形。
对同一个文法而言,LALR分析表和SLR分析表的状态个数相同。
两个LR(1)项目集是同心的:若除了搜索符外,这两个集合是相同的。
我们试图将所有同心的LR(1)项目集,合并为一个项目集。目的是希望能减少些状态个数。
但可能会存在这种现象:有一个LR(1)文法,它的所有LR(1)项目集都不存在冲突,但同心集合并后会存在“归约-归约”冲突 。
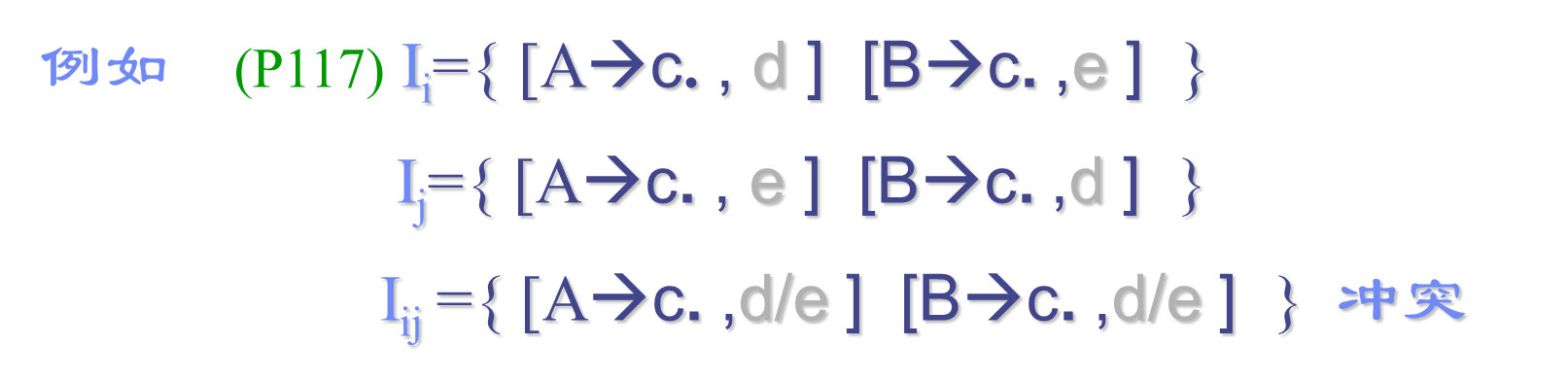
合并同心集后对某些错误发现的时间会产生推迟现象;
当输入串有误时,LR(1)能够及时发现错误,而 LALR 则可能还继续执行一些多余的归约动作,但决不会执行新的移进。
这意味着 LALR(1) 分析表比 LR(1) 分析表对同一输入串的分析可能会有多余归约。
但错误的出现位置仍是准确的。
LALR分析表的构造算法


●LALR分析表:按上述算法构造的分析表,若没有多重定义入口,则称为LALR分析表。
● LALR(1)文法:具有LALR分析表的文法。
例题








结论
●若文法是LR(0)的,则一定是SLR(1)的。反之不一定
●若文法是LALR(1)的,则一定是LR(1)的。反之不一定
●所有LR文法都是无二义的。
四种 LR 文法的判别方法:
首先判别文法是否为二义性文法,任何二义性文法都不是 LR 类文法。然后根据项目集中是否含冲突项目或相应分析表中是否含多重定义元素进行判断:
(a)LR(0) 文法是所有 LR(0) 项目集中没有“移进-归约”或“归约-归约”冲突(或 LR(0)分析表中不含多重定义)。
(b)SLR(0) 文法是 **LR(0) 项目集中含有冲突的项目都能用 SLR 规则解决(**或 SLR(0)分析表中不含多重定义)。
(c)LR(1) 文法是所有 LR(1) 项目集中 没有“移进-归约”或“归约-归约”冲突(或LR(1)分析表中不含多重定义)。
(d)LALR(1) 项目集中 无“归约-归约”冲突(或LALR(1)分析表中不含多重定义)。注意搜索符只对归约项目起作用。
四种文法的关系:
一个文法是 LR(0) 文法,一定也是 SLR(1) 文法,也是 LR(1) 文法和 LALR(1) 文法。