题目

332.重新安排行程【困难】

题解

这道题的几个难点：

一个行程中，如果航班处理不好容易变成一个圈，成为死循环
有多种解法，字母序靠前排在前面，应该如何记录映射关系？
使用回溯法，终止条件是什么？
搜索的过程中，如何遍历一个机场所对应的所有机场？

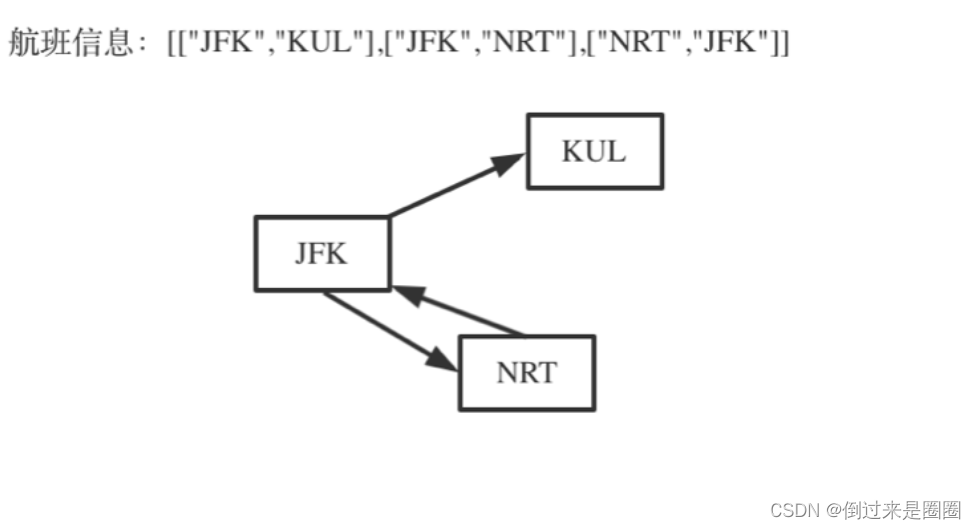
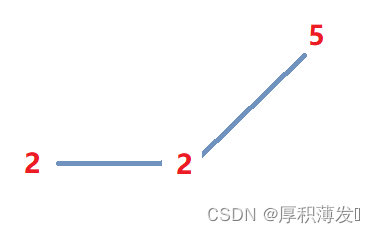
如何理解死循环

如图情况，若没有处理好，可能在JFK和NRT之间形成死循环
在这里插入图片描述

如何记录映射关系

一个机场映射多个机场，机场之间要靠字母序排列，可以使用HashMap记录
定义如下：

Map<String,Map<String, Integer>>map：Map<出发机场，Map<到达机场，航班次数>>map

为什么一定要增删元素呢？因为出发机场和到达机场会重复，搜索的过程没及时删除目的机场就会死循环。

在遍历Map<出发机场，Map<到达机场，航班次数>>map过程中，可以使用“航班次数”这个字段做加减，来标记到达机场是否使用过了。

如果“航班次数”大于0，说明目的地还可以飞，如果“航班次数”等于0说明目的地不能飞了，而不用对集合做删除元素或者增加元素的操作。（相当于说我不删，我就做一个标记！）

回溯法

递归树

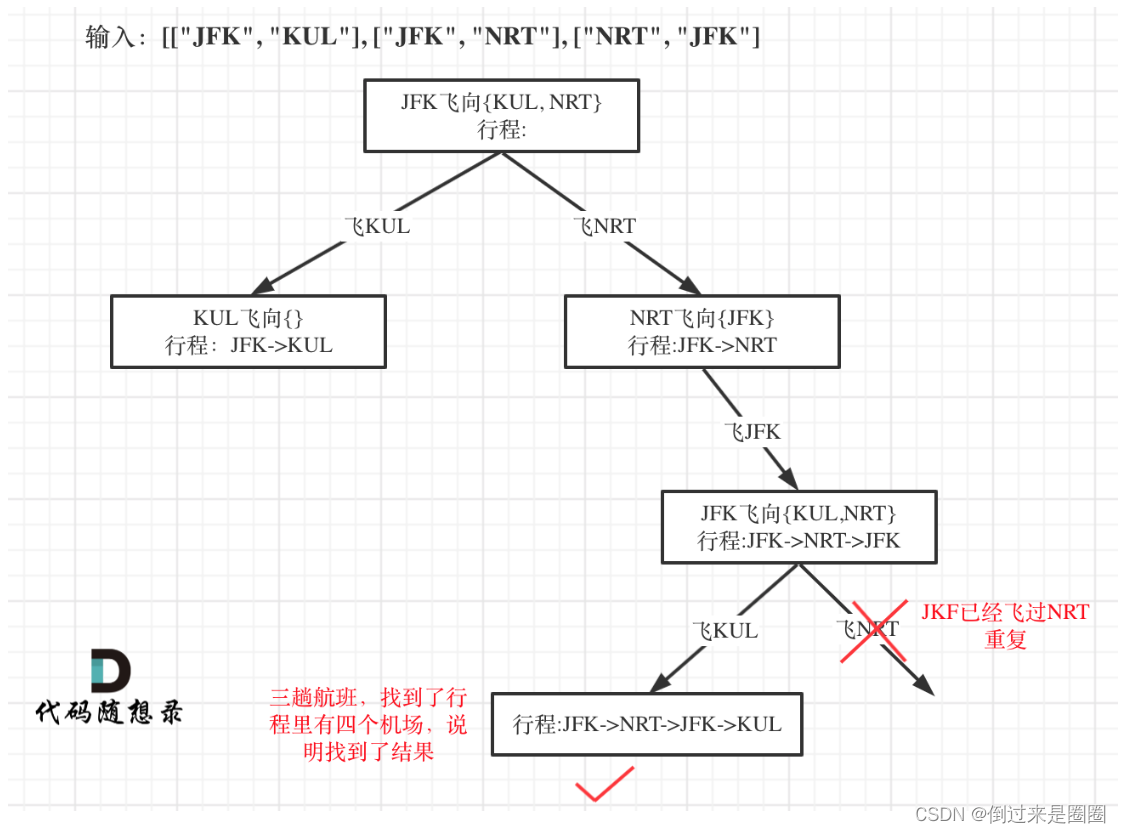
在这里插入图片描述

回溯三部曲

递归函数参数
使用Map<出发机场，Map<到达机场，航班次数>>map记录航班的映射关系

注意这里函数返回值是boolean！而不是通常用的void！

因为我们只需要找到一个行程，就是在树形结构中唯一一条通向叶子节点的路线，如上递归树所示。

递归终止条件
回溯过程中遇到的机场个数，达到了（航班数量+1），就找到了一个行程，将所有航班串在一起了。

if(res.size()==n+1){
   return;
}

单层搜索过程
回溯的过程中，如何遍历一个机场所对应的所有机场呢？

for (pair<const string, int>& target : targets[result[result.size() - 1]]) {
    if (target.second > 0 ) { // 记录到达机场是否飞过了
        result.push_back(target.first);
        target.second--;
        if (backtracking(ticketNum, result)) return true;
        result.pop_back();
        target.second++;
    }
}

完整代码

回溯法代码实在是太麻烦了，还是换成官方题解的“Hierholzer 算法" 了，用于在连通图中找欧拉路径。

对于航班映射关系的存储和上面不同，对于java来说这种写法简便很多，也方便删除！

class Solution {
    List<String>res=new ArrayList<>();
    Map<String,PriorityQueue<String>>map=new HashMap<>();//记录航班映射关系
    public List<String> findItinerary(List<List<String>> tickets){
        int n=tickets.size();
        //初始化航班映射关系
        for(List<String>ticket:tickets){
            String src=ticket.get(0),dest=ticket.get(1);
            //首次存入新建优先队列
            if(!map.containsKey(src))
                map.put(src,new PriorityQueue<>());
            map.get(src).add(dest);
        }
        //深搜
        dfs("JFK");
        Collections.reverse(res);//最先找到的是最深的不能再走的目的地，所以要反转过来
        return res;
    }
    public void dfs(String src){
        //当传入的参数是始发地而且还有边的时候，取边出队删除并且继续递归深搜这条边的点，一直到不能再走再返回
        while(map.containsKey(src)&&map.get(src).size()>0)
            dfs(map.get(src).poll());
        res.add(src);
    }
}