计算机视觉算法——基于深度学习的高精地图算法（HDMapNet / VectorMapNet / MapTR / VectorNet）

高精地图广泛应用于自动驾驶领域，传统的高精地图构建和使用算法通常是基于SLAM实现的，但是最近两年出现了很多基于深度学习的方法，例如HDMapNet、VectorMapNet和MapTR就介绍了如何通过NN直接利用感知信息构建矢量化的高精地图，而VectorNet介绍了如何使用NN直接对矢量化的高精地图信息进行编码，从而能高效地作为一路输入被系统所利用。下面

1. HDMapNet

HDMapNet为2021年发表的文章，原论文名为《HDMapNet: An Online HD Map Construction and Evaluation Framework》，该论文的主要目的是利用自动驾驶车辆上的环视相机和激光雷达对BEV视角下的地图元素进行矢量化。

1.1 网络结构及特点

网络结构如下图所示：

整个网络结构主要有Image and Point Cloud Encoder和Bird’s-eye View Decoder构成，输出分割结构后通过后处理输出结构化地图元素。

1.1.1 Image and Point Cloud Encoder

相机输入图片通过一个权重共享的特征提取网络编码为特征图${\mathcal{F}}_{{\mathcal{I}}_i}^{\mathrm{pv}}\subseteq {\mathbb{R}}^{H_{\mathrm{pv}}\times W_{\mathrm{pv}}\times K}$，然后通过MLP将特征图映射到BEV下，方法类似VPN，不同的是在本论文中显示地使用了相机的外参：$${\mathcal{F}}_{{\mathcal{I}}_i}^c[h][w]={\varphi }_{{\mathcal{V}}_i}^{hw}\left({\mathcal{F}}_{{\mathcal{I}}_i}^{\mathrm{pv}}[1][1],\dots ,{\mathcal{F}}_{{\mathcal{I}}_i}^{\mathrm{pv}}\left[H_{\mathrm{pv}}\right]\left[W_{\mathrm{pv}}\right]\right)$$其中${\varphi }_{{\mathcal{V}}_i}^{hw}$建立了从前视图特征到BEV特征的映射关系，最后在BEV下通过相机的外参将各个相机的特征进行加权平均。

激光的编码使用的PointPillar的方法，首先将三维空间划分为多个Pillar，使用PointNet将同一个Pillar中的激光点处理成特征： f j pillar  = PN ⁡ ( { f p ∣ ∀ p ∈ P j } ) f_j^{\text {pillar }}=\operatorname{PN}\left(\left\{f_p \mid \forall p \in P_j\right\}\right) fjpillar ​=PN({fp​∣∀p∈Pj​})最后通过卷积网络${\varphi }_{\text{pillar }}$在BEV下对Pillar进行进一步特征提取得到${\mathcal{F}}_P^{\mathrm{bev}}$。

1.1.3 Bird’s-eye View Decoder

解码部分使用的Backbone是FCN，然后接三个输出头，其中第一个输出头进行车道语义分割；第二个输出头进行车道实例分割；第三输出头进行车道方向预测，这里我们详细介绍下车道实例分割和车道方向预测的设计：
车道实例分割是基于Instance Embedding实现，即同一个车道实例网络应该输出相同或接近的Instance Embedding，Instance Embedding的Loss定义如下：$$L_{var}=\frac{1}{C}\sum _{c=1}^C\frac{1}{N_c}\sum _{j=1}^{N_c}{\left[\Vert {\mu }_c-f_j^{\mathrm{instance}}\Vert -{\delta }_v\right]}_{+}^2$$$$L_{dist}=\frac{1}{C(C-1)}\sum _{c_A\ne c_B\in C}{\left[2{\delta }_d-\Vert {\mu }_{c_A}-{\mu }_{c_B}\Vert \right]}_{+}^2,$$$$L=\alpha L_{var}+\beta L_{\text{dist }}.$$其中$L_{var}$为方差损失，$L_{dist}$为距离损失。$C$为真值中车道实例的个数，$f_j^{\mathrm{instance}}$为第$j$个预测为实例$c$的Instance Embedding，$N_c$为预测为第c个车道实例中的像素个数，${\mu }_c$为预测为第c个车道实例中像素的均值，$\Vert \cdot \Vert$为$L2$归一化，$[x{]}_{+}=\max (0,\mathrm{x})$，${\delta }_v$和${\delta }_d$分别为方差损失和距离损失的裕度。方差损失损失函数的大概含义就是使得同一个车道实例的Instance Embedding尽可能接近，而距离损失则是使得不同车道实例的尽可能不同。

车道方向预测定义如下：
方向的预测的目标是预测车道线上每一个像素$C$的方向，实际上是定义了一系列用于描述方向的节点，每个节点将方向划分为$N_d$个类别，假定当前节点的方向为$C_{now}$，那么下一个节点的方向为$C_{next}=C_{now}+{\Delta }_{step}\cdot D$，其中${\Delta }_{step}$为预先定义好的步长。由于我们在预测的时候并不知道当前节点方向，因此我们需要同时预测前向和后向节点的方向，因此每个节点方向的真值是一个长为$N_d$的向量，向量中只有两个值为1，其他的均为0，最后车道方向计算的是一个分类损失。（这一部分通过论文解释其实理解得不是很透彻，实践的时候还是要结合代码具体看下）

在HDMapNet中最后是通过一系列后处理来讲分割结果进行矢量化的，首先使用DBSCAN算法对Instant Embedding进行聚类，然后通过NMS算法减少冗余，最后通过方向使用贪婪算法进行连通域搜寻输出矢量化结果。（这一部分也需要结合代码才能了解到细节）

1.2 实验结果

论文中对IPM，Lift-Splat-Shoot，VPN经典算法进行了可对比，同时对激光和视觉输入进行了Ablation Study，可以看到，激光和视觉融合的HDMapNet效果是最好的。

以上是可视化结果，其中IPM是直接将PV的分割结果通过逆透视变换投影到BEV下；IPM(B)是先将PV图投影到BEV下，然后在BEV下进行分割；IPM(CB)是在PV进行特征提取，将提取的特征图投影到BEV下进行解码；Lift-Splat-Shoot是通过预测的深度显示地将2D图片转化为3D点云特征，并最终映射到BEV下；VPN是通过MLP将PV上的特征映射到BEV下；定量结果如下：

2. VectorMapNet

VecotrNetMap发表于2022年，原论文名为《VectorMapNet: End-to-End Vectoried HD Map Learning》，该论文的主要贡献是实现了一个端到端输出矢量化地图元素的网络。

2.1 网络结构及特点

网络结构如下图所示：

VectorMapNet对激光输入和视觉输入的编码和HDMapNet类似，在此就不再赘述，这里主要介绍下上图中展示的Map Element Detector以及Polyline Generator这两部分。

2.1.1 Map Element Detector

在VectorNetMap中所有地图元素都通过Polyline进行表达。Map Element Detector的作用主要是在BEV feature中检测出关键点$A_i=\left\{a_j\in {\mathbb{R}}^2\mid j=1,\dots ,k\right\}$，这些关键点并不是网络最后输出的Polyline的采样点，而仅仅是对地图元素轮廓的一种描述。这些关键点输入Polyline Generator进一步Decoder最后才得到的Polyline上的采样点。

具体而言，论文中使用的是一种类似DETR的方式，通过Element Queries $\{q_i^{\text{elem }}\in {\mathbb{R}}^{k\times d}\mid i=1,\dots ,N_{\max }\}$与BEV Feature进行一系列Cross Attention和Self Attention。其中，每个Element Query由$k$个可学习的Query Embedding组成，即$q^{\mathrm{kp}}:q_i^{\text{elem }}=\left\{q_{i,j}^{\mathrm{kp}}\in {\mathbb{R}}^d\mid j=1,\dots ,k\right\}$。为了节省计算量，作者这里采用的Deformable Attention Module，关于Deformable Attention Module的相关知识可以参考计算机视觉算法——基于Transformer的目标检测（DETR / Deformable DETR / DETR 3D）。Query Embedding最后通过两个MLP分别回归出关键点坐标$a_{i,j}={\mathrm{MLP}}_{\mathrm{kp}}\left(q_{i,j}^{\mathrm{kp}}\right)$和类别$l_i={\mathrm{MLP}}_{\mathrm{cls}}\left(\left[q_{i,1}^{\mathrm{kp}},\dots ,q_{i,k}^{\mathrm{kp}}\right]\right)$，其中$[\cdot ]$表示Concatenate操作。

2.1.2 Polyline Generator

Polyline Generator的目标是生成地图元素轮廓的细节，Polyline Generator是对Polyline生成一个坐标分布$p\left(V_i^{\mathrm{poly}}\mid a_i,l_i,{\mathcal{F}}_{\mathrm{BEV}}^f\right)$，即在知道关键点$a_i$，类别$l_i$和BEV特征${\mathcal{F}}_{\mathrm{BEV}}$的先验下估计出Polyline的坐标分布$p(V_i^{\mathrm{poly}})$，而Polyline的坐标分布可以由一系列采样点的坐标分布点乘获得：$$p\left(V_i^{\mathrm{poly}}\mid a_i,l_i,{\mathcal{F}}_{\mathrm{BEV}};\theta \right)=\prod _{n=1}^{2N_v}p\left(v_{i,n}^f\mid v_{i,<n}^f,a_i,l_i,{\mathcal{F}}_{\mathrm{BEV}}\right)$$作者在论文做了这样一堆解释其实就是为了说明其Polyline Generator模块的合理性，正是上述分布的点乘特性，因此Polyline Generator可以设计为自回归网络，逐个输入Query并逐个输出采样点的坐标值直到序列结束标记EOS。

Polyline Generator的输入三种Query：第一种和第二种分别是由Map Element Detector输出的KeyPoint和Label通过Tokenized得到Embedding；第三种则是可学习的Polyline Embedding，由Coordinate Embedding、Position Embedding和Value Embedding构成，Coordinate Embedding代表这个坐标是x还是y，Position Embedding代表这个向量属于哪个Token，Value Embedding代表这个Token的量化坐标值。Polyline Embedding逐个输入到Polyline Generator模块，逐个输出的Embedding通过MLP后解析出对应的坐标，直到输出坐标值直到序列结束标记EOS。如下图所示：
输入前两种Query：

输入第一个Query：

输入第二个Query：

输入第三个Query：

依次类推，这样输出的Polyline的长度理论上是没有限制的。

2.1.3 Training Loss

VectorMapNet Loss一共由Map Element Detector和Polyline Generator两部分构成，其中Map Element Detector的损失使用的是参考DETR的Bipartite Matching Loss。Polyline Generator Loss目标是最大化Polyline的对数分布概率，因此使用的负的对数似然，即$${\mathcal{L}}_{gen}=-\frac{1}{2N_v}\sum _{n=1}^{2N_v}\log \hat{p}\left(v_{i,n}^f\mid v_{i,<n}^f,a_i,l_i,{\mathcal{F}}_{\mathrm{BEV}}^f\right)$$其中，$\hat{p}\left(v_{i,n}^f\mid \dots \right)$为坐标值的条件概率，$v_{i,<n}^f$指的是index小于$n$的离散坐标值真值。对于Polyline Generator的训练策略是先用真值坐标作为输入进行训练，然后再使用预测的坐标点进行finetune。

2.2 实验结果

作者对HDMapNet和VectorMapNet的结果进行了可视化对比如下：

可以看到VectorMapNet的输出在拐角处更加锐利，对于普通的车道线输出则更加平滑，这正是Polyline输出带来的收益。；同时从第三行的对比结果也可以看出，VectorNetMap可以对更加细节的轮廓进行表达，作者认为这是将地图元素通过检测的方法输出带来的收益。以上方法定量的对比结果如下：

3. MapTR

MapTR是2022年发表的论文，原论文名为《MapTR: Structed Modeling And Learning for Online Vectorized HD Map Construction》，是在VectorNetMap基础上做了进一步改进，论文上来就先指出了VectorMapNet的问题，一共由如下三点：
（1）VectorMapNet中是通过Polyline表征地图元素，对于Polyline的方向或者说起止点的定义在某些场景下是不明确的，例如斑马线，如果用Polyline进行表征，其起止点可以有多种定义，这对于网络学习的真值来说是一个很难定义成一个通用标准。
（2）VectorMapNet虽然可以并行输出所有的Polyline，但是是通过循环的方式逐个预测出Polyline上的采样点，这样使得推理时间变长。
（3）VectorMapNet使用的是自回归的解码器，这使得预测的过程存在累计误差，同时使得网络更难收敛，需要更长的训练时间

3.1 网络结构及特点

MapTR的网络结构如下图所示：

整个论文是基于DETR开发的，Encoder和2D to BEV的部分就不再赘述，作者在论文中一共对比了IPM、LSS、Deformable Attention、GTK四种2D to BEV的方法。下面主要介绍Map Decoder和类似于DETR种的二分匹配过程的设计。

3.1.1 Map Decoder

与DETR不同的是，在MapTR中使用的是Hierachical Query从BEV Feature中获取地图元素，所谓Hierachical Query指的是作者分别定义了Instance-Level Query ${\left\{q_i^{(\mathrm{ins})}\right\}}_{i=0}^{N-1}$和Point-Level Qurey ${\left\{q_j^{(\mathrm{pt})}\right\}}_{j=0}^{N_v-1}$，然后每一个地图元素的Hierachical Query ${\left\{q_{ij}^{\text{(hie) }}\right\}}_{j=0}^{N_v-1}$有这两种Query组成，即第$i$个Instant Query和第$j$个Point Query：$$q_{ij}^{(\mathrm{hie})}=q_i^{(\mathrm{ins})}+q_j^{(\mathrm{pt})}$$MapTR最后预测头很简单，包括一个分类分支和一个坐标点回归分支，分类分支用于判定该输出属于哪个实例，回归分支用于预测具体的点坐标位置

3.1.2 Permutation-Based Modeling and Matching

MapTR将地图元素分为Closed Shape和Open Shape，Closed Shape可以用Polygon表达，Open Shape可以用Polyline表达。Polygon和Polyline又都可以通过一系列有顺序的点集表达$V^F=\left[v_0,v_1,\dots ,v_{N_v-1}\right]$，其中$N_v$是点集的数量。然后点集的排列顺序确实不确定的，MapTR中映入了排列顺序 Γ = { γ k } \Gamma=\left\{\gamma_k\right\} Γ={γk​}这一变量来消除这一不确定性，其中${\gamma }_k$为第$k$种排列可能。

对于Polyline，一共又两种排列顺序，即一个超前一个朝后： Γ polyline  = { γ 0 , γ 1 } { γ 0 ( j ) = j   m o d   N v γ 1 ( j ) = ( N v − 1 ) − j   m o d   N v \Gamma_{\text {polyline }}=\left\{\gamma_0, \gamma_1\right\}\left\{\begin{array}{l} \gamma_0(j)=j \bmod N_v \\ \gamma_1(j)=\left(N_v-1\right)-j \quad \bmod N_v \end{array}\right. Γpolyline ​={γ0​,γ1​}{γ0​(j)=jmodNv​γ1​(j)=(Nv​−1)−jmodNv​​对于Polygan，一共有$2\times N_v$种排列顺序： Γ polygon  = { γ 0 , … , γ 2 × N v − 1 } { γ 0 ( j ) = j   m o d   N v , γ 1 ( j ) = ( N v − 1 ) − j   m o d   N v γ 2 ( j ) = ( j + 1 )   m o d   N v , γ 3 ( j ) = ( N v − 1 ) − ( j + 1 )   m o d   N v , … γ 2 × N v − 2 ( j ) = ( j + N v − 1 )   m o d   N v , γ 2 × N v − 1 ( j ) = ( N v − 1 ) − ( j + N v − 1 )   m o d   N v \Gamma_{\text {polygon }}=\left\{\gamma_0, \ldots, \gamma_{2 \times N_v-1}\right\}\left\{\begin{array}{l} \gamma_0(j)=j \bmod N_v, \\ \gamma_1(j)=\left(N_v-1\right)-j \bmod N_v \\ \gamma_2(j)=(j+1) \bmod N_v, \\ \gamma_3(j)=\left(N_v-1\right)-(j+1) \bmod N_v, \\ \ldots \\ \gamma_{2 \times N_v-2}(j)=\left(j+N_v-1\right) \bmod N_v, \\ \gamma_{2 \times N_v-1}(j)=\left(N_v-1\right)-\left(j+N_v-1\right) \bmod N_v \end{array}\right. Γpolygon ​={γ0​,…,γ2×Nv​−1​}⎩ ⎨ ⎧​γ0​(j)=jmodNv​,γ1​(j)=(Nv​−1)−jmodNv​γ2​(j)=(j+1)modNv​,γ3​(j)=(Nv​−1)−(j+1)modNv​,…γ2×Nv​−2​(j)=(j+Nv​−1)modNv​,γ2×Nv​−1​(j)=(Nv​−1)−(j+Nv​−1)modNv​​基于这种定义，MapTR使用Hierarchical Bipartite Matching来进行结果匹配和损失计算。

Hierarchical Bipartite Matching一共分为两部分，分别是Instance-Level Matching和Point-Level Matching：
Instance-Level Matching指的是将预测的地图元素类别 { y ^ i } \left\{\hat{y}_i\right\} {y^​i​}和真值的地图元素类别 { y i } \left\{y_i\right\} {yi​}进行最优匹配，假设预测的地图元素数量为$N$，那么匹配结果就是一个长为$N$的排列结果，定义Instance-Level Matching的损失函数如下：$$\hat{\pi }=\underset{\pi \in {\Pi }_N}{\mathrm{argmin}}\sum _{i=0}^{N-1}{\mathcal{L}}_{\text{insmatch }}\left({\hat{y}}_{\pi (i)},y_i\right)$$$${\mathcal{L}}_{\text{insmatch }}\left({\hat{y}}_{\pi (i)},y_i\right)={\mathcal{L}}_{\text{Focal }}\left({\hat{p}}_{\pi (i)},c_i\right)+{\mathcal{L}}_{\text{position }}\left({\hat{V}}_{\pi (i)},V_i\right)\text{. }$$其中${\mathcal{L}}_{\text{Focal }}\left({\hat{p}}_{\pi (i)},c_i\right)$是类别损失函数，使用的是Focal Loss。${\mathcal{L}}_{\text{position }}\left({\hat{V}}_{\pi (i)},V_i\right)$是位置损失函数，反映的是点集之间的距离，MapTR一共尝试了两种损失函数，分别是Chamfer Distance和Point2Point距离。Point2Point距离和Point-Level Matching Cost很接近，即先寻找最优的点到点的匹配，然后计算所有匹配点的曼哈顿距离。在实验种Point2Point距离要更好。

Point-Level Matching指的是对匹配好的地图元素种的每个点进行匹配，目标是找到一个排列$\hat{\gamma }\in \Gamma$使得对应的点之间的曼哈顿距离之和最小：$$\hat{\gamma }=\underset{\gamma \in \Gamma }{\mathrm{argmin}}\sum _{j=0}^{N_v-1}{D}_{\text{Manhattan }}\left({\hat{v}}_j,v_{\gamma (j)}\right).$$

在找到Instant-Level和Point-Level的最优匹配之后，最后就是根据最优匹配的结果进行损失计算，损失计算公式如下：$$\mathcal{L}=\lambda {\mathcal{L}}_{\mathrm{cls}}+\alpha {\mathcal{L}}_{\mathrm{p}2\mathrm{p}}+\beta {\mathcal{L}}_{\mathrm{dir}}$$其中${\mathcal{L}}_{\mathrm{cls}}$为分类损失，和DETR一样，分类类别中除了正常的真值类别外还会添加一种no object类别，使用的Focal Loss：$${\mathcal{L}}_{\mathrm{cls}}=\sum _{i=0}^{N-1}{\mathcal{L}}_{\text{Focal }}\left({\hat{p}}_{\hat{\pi }(i)},c_i\right)$$${\mathcal{L}}_{\mathrm{p}2\mathrm{p}}$为距离损失，使用的曼哈顿距离： L p 2 p = ∑ i = 0 N − 1 1 { c i ≠ ∅ } ∑ j = 0 N v − 1 D Manhattan  ( v ^ π ^ ( i ) , j , v i , γ ^ i ( j ) ) \mathcal{L}_{\mathrm{p} 2 \mathrm{p}}=\sum_{i=0}^{N-1} \mathbb{1}_{\left\{c_i \neq \varnothing\right\}} \sum_{j=0}^{N_v-1} D_{\text {Manhattan }}\left(\hat{v}_{\hat{\pi}(i), j}, v_{i, \hat{\gamma}_i(j)}\right) Lp2p​=i=0∑N−1​1{ci​=∅}​j=0∑Nv​−1​DManhattan ​(v^π^(i),j​,vi,γ^​i​(j)​)${\mathcal{L}}_{\mathrm{dir}}$为方向距离，使用是余弦相似度： L d i r = − ∑ i = 0 N − 1 1 { c i ≠ ∅ } ∑ j = 0 N v − 1 cosine ⁡ S − similarity ⁡ ( e ^ π ^ ( i ) , j , e i , γ ^ i ( j ) ) \mathcal{L}_{\mathrm{dir}}=-\sum_{i=0}^{N-1} \mathbb{1}_{\left\{c_i \neq \varnothing\right\}} \sum_{j=0}^{N_v-1} \operatorname{cosine} \mathrm{S}_{-} \operatorname{similarity}\left(\hat{\boldsymbol{e}}_{\hat{\pi}(i), j}, \boldsymbol{e}_{\boldsymbol{i}, \hat{\gamma}_i(j)}\right) Ldir​=−i=0∑N−1​1{ci​=∅}​j=0∑Nv​−1​cosineS−​similarity(e^π^(i),j​,ei,γ^​i​(j)​)$${\hat{\mathbf{e}}}_{\hat{\pi }(i),j}={\hat{v}}_{\hat{\pi }(i),j}-{\hat{v}}_{\hat{\pi }(i),(j+1){\mathrm{modN}}_{\mathrm{v}}}$$$${\mathbf{e}}_{\mathbf{i},{\hat{\gamma }}_i(j)}=v_{i,{\hat{\gamma }}_i(j)}-v_{i,{\hat{\gamma }}_i(j+1){\mathrm{modN}}_{\mathrm{v}}}$$

3.2 实验结果

作者首先对比和HDMapNet以及VectorMapNet的结果如下：

可以看到MapTR在速度和精度上都有明显提升，可视化结果如下，看上去还是非常惊艳的：

4. VectorNet

VectorNet为Waymo在20202年发表的论文，原论文名为《VectorNet: Encoding HD Maps and Agent Dynamics from Vectorized Representation》，这是一篇做预测的工作，前面介绍的都是如果通过感知构建高精地图，重点在于“建”，而这篇文章重点在于“用”，

在车辆行驶过程中，其未来轨迹主要是受到周围静态环境以及其他行驶车辆的影响。因此在预测任务中，我们通常需要同时对局部的高精地图以及周围的其他车辆轨迹进行编码。本文核心贡献是则是提出了一种对高精地图进行矢量化编码的方法（如上图右所示），相对于传统的渲染图+卷积的编码方式（如果上图左所示）效率更好，效果也更好。

4.1 网络结构及特点

我将论文中介绍的方法抽象为三步，第一步是将图节点的特征提取出来（Graph Node Encoder），第二步对图中节点的特征进行交互（Graph Node Interaction），第三步是对交互的特征进行解码获得最后的输出（Graph Node Decoder）：

4.1.1 Graph Node Encoder

对于高精地图，其元素通常由多段线（车道线）、闭包（人行道）以及点（交通灯）构成，这些元素通常都会带有语义和状态这样的附属信息。对于这些元素，我们选取一个起始点以及一个方向，然后再曲线上进行等间距采样，采样点按顺序相连就得到向量，而向量就是论文中用于编码的最小单位，被称为节点。
对于车辆轨迹，其元素组成主要就是多段线。我们可以以时刻为0的位置为起点，然后等时间间隔进行采样，将相邻采样点构成的向量同样作为节点输入后续网络进行编码。
因此我们可以统一使用如下的公式对节点进行描述：$${\mathbf{v}}_i=\left[{\mathbf{d}}_i^s,{\mathbf{d}}_i^e,{\mathbf{a}}_i,j\right]$$其中${\mathbf{d}}_i^s$和${\mathbf{d}}_i^e$分别是该节点的起点和终点坐标$(x,y,z)$，为了使得节点的特征和位置无关，还需要对节点的坐标以自车坐标进行归一化操作。${\mathbf{a}}_i$为该节点的附属信息，例如车道线的类别，轨迹的时间戳等。$j$指的是该节点属于第$j$条曲线。

为了充分利用多段线的语义和空间特征，对于具备$p$个节点 { v 1 , v 2 , … , v P } \left\{\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_P\right\} {v1​,v2​,…,vP​}的多段线$\mathcal{P}$，我们设计如下操作进行特征提取：$${\mathbf{v}}_i^{(l+1)}={\phi }_{\mathrm{rel}}\left(g_{\mathrm{enc}}\left({\mathbf{v}}_i^{(l)}\right),{\phi }_{\mathrm{agg}}\left(\left\{g_{\mathrm{enc}}\left({\mathbf{v}}_j^{(l)}\right)\right\}\right)\right)$$其中${\mathbf{v}}_i^{(l)}$为第$l$层节点特征，$g_{\mathrm{enc}}(\cdot )$为对所有节点权重共享的多层感知机，具体为一个全连接层、一个Layer Normalization层和ReLU非线性激活层。${\phi }_{\text{agg }}(\cdot )$为Max Pooling操作。${\phi }_{\mathrm{rel}}(\cdot )$为Concatenate操作，完成的流程图如下图所示：

我们将以上结构叠加多层得到各个节点的特征，最后为了得到多段线节点的特征，我们通过Max Pooling对各个节点进行提取：$$\mathbf{p}={\phi }_{\mathrm{agg}}\left(\left\{{\mathbf{v}}_i^{\left(L_p\right)}\right\}\right)$$以上我们就得到各个多段线的特征。

4.1.2 Graph Node Interaction

接下来我们需要通过一个全局GNN网络对各个多段线之间的特征 { p 1 , p 2 , … , p P } \left\{\mathbf{p}_1, \mathbf{p}_2, \ldots, \mathbf{p}_P\right\} {p1​,p2​,…,pP​}进行交互：$$\left\{{\mathbf{p}}_i^{(l+1)}\right\}=\mathrm{GNN}\left(\left\{{\mathbf{p}}_i^{(l)}\right\},\mathcal{A}\right)$$其中$\mathcal{A}$是各个多段线之间的邻接矩阵，可以设置为各个多段线之间的距离。在论文中，为了简化计算，直接将$\mathcal{A}$设置为全连接矩阵，GNN网络通过Self-Attention代替$$\mathrm{GNN}(\mathbf{P})=\mathrm{softmax}\left({\mathbf{P}}_Q{\mathbf{P}}_K^T\right){\mathbf{P}}_V$$其中${\mathbf{P}}_Q,{\mathbf{P}}_K$和${\mathbf{P}}_V$为特征$\mathbf{P}$的特征映射。

4.1.3 Graph Node Decoder

经过GNN后，最后通过Decoder对未来轨迹进行预测：$${\mathbf{v}}_i^{\text{future }}={\phi }_{\text{traj }}\left({\mathbf{p}}_i^{\left(L_t\right)}\right)$$其中$p_i^{\left(L_t\right)}$为GNN网络的第$L_t$层输出，${\phi }_{\text{traj }}$为MLP。为了使得GNN网络能够更好地学习到各个模块之间的关系，论文中还使用了类似于自然语言处理模型BERT中的掩码机制辅助训练，具体操作是在训练过程中给随机Mask掉一些节点，然后通过Decoder对该节点进行恢复：$${\hat{\mathbf{p}}}_i={\phi }_{\text{node }}\left({\mathbf{p}}_i^{\left(L_t\right)}\right)$$其中${\phi }_{\text{node }}$同样是MLP。在推理过程中该Decoder是不使用的。

4.1.4 Training Loss

VectorNet的Loss由两部分构成：$$\mathcal{L}={\mathcal{L}}_{\text{traj }}+\alpha {\mathcal{L}}_{\text{node }}$$其中${\mathcal{L}}_{\text{traj }}$为预测轨迹真值Loss，具体为负高斯对数似然损失；${\mathcal{L}}_{\text{node }}$为预测节点和真值之间的Huber Loss。在节点特征进入节点交互流程之前，会使用$L2$归一化处理一遍来限制${\mathcal{L}}_{\text{node }}$的幅值大小。

4.2 实验结果

在论文中，作者除了介绍了上述基于矢量编码和GNN的方法，还介绍了一种基于渲染编码的基线方法。基于基线的方法就是将临近的10帧结果渲染成$S\times S\times 3$大小的图片，在将其叠加在一起得到$S\times S\times 3N$的输入。是然后使用ResNet去提取特征，通过全连接层输出。作者在论文中将VectorNet和这种基线方法对比结果如下：

对比的指标为Average Displacement Error，计算整条轨迹在$3$秒时刻的距离误差。可以看到VectorNet在计算量和精度上都远由于基线版本。实际输出结果如下：

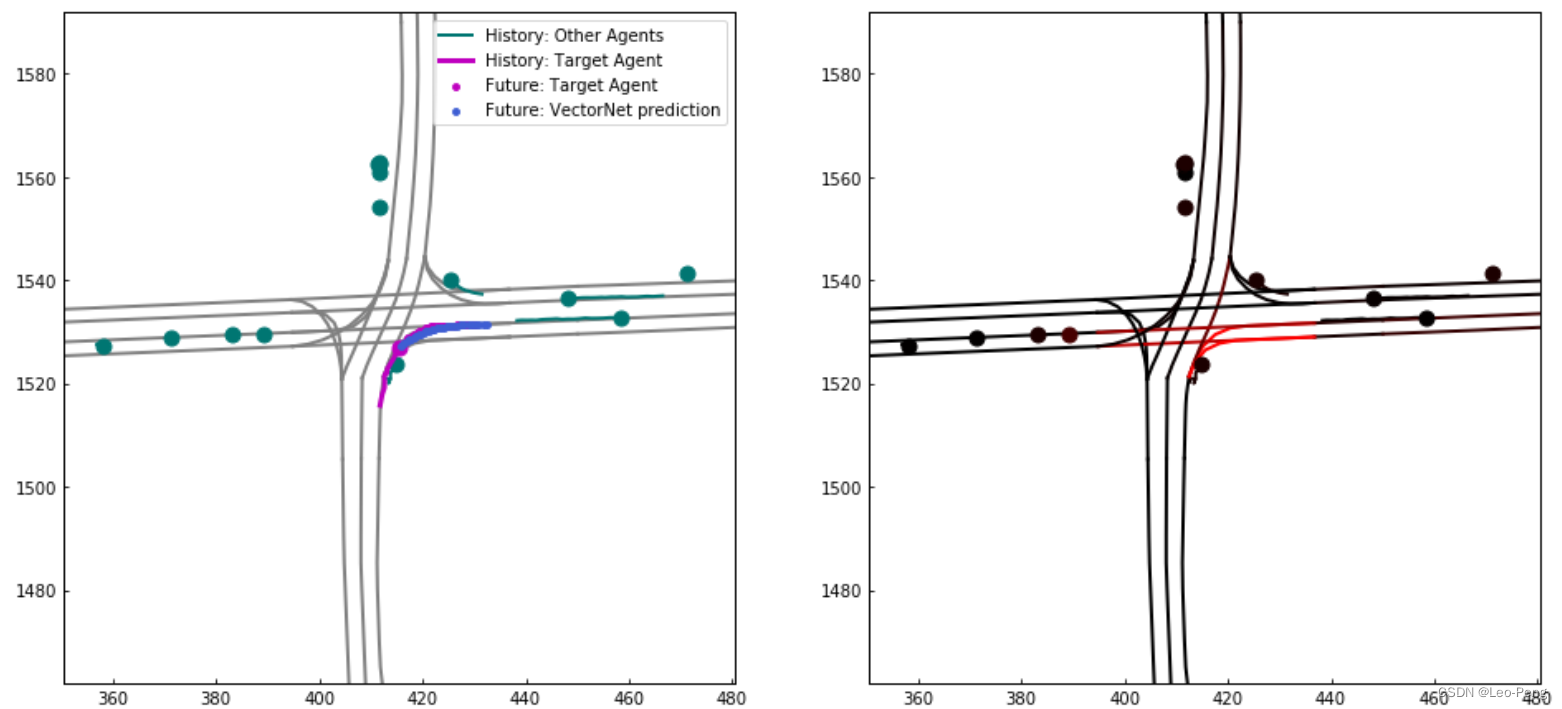
其中上左图紫红色线为历史车流结果，而蓝色点为预测车流结果，紫红色点真是车流结果。蓝色点基于将紫红色点覆盖，说明这个案例下模型预测成功。上右图中越红是区域说明模型注意力越高，可视化结果也说明模型将注意力的确集中到了两条正确的右转车道上。